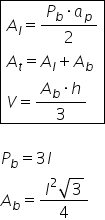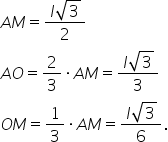Piramida triunghiulară regulată (aplicații)
Tag-uri
Partajeaza in Google Classroom

Transcript
să rezolvăm acum o aplicație cu
piramida triunghiulară regulată
și avem această problemă între
o piramidă triunghiulară regulată
se dă înălțimea de 4 cm metri deci
o are 4 cm și măsura diedrului
format de o față laterală cu planul
bazei este de 30 de grade să aflăm
aria laterală aria totală și volumul
Ce este acela diedru pentru că
se spune măsura diedrului format
de o față laterală cu planul bazei
pe Să ne amintim că un unghi diedru
este un unghi format de două plane
și planele care sunt date aici
Sunt o față laterală de exemplu
va acesta an și planul bazei deci
a b c care este unghiul făcut de
planele V a b și a b c d pentru
aceasta trebuie să construim un
unghi plan al diedrului adică pe
muchia comună a celor două plane
adică muchia diedrului care aici
este a b a b este dreapta cuprinsă
inclusă în planul vab și în planul
abc pe această muchia diedrului
trebuie să alegem un punct iar
în punctul respectiv vom duce o
perpendiculară pe dreapta ab acea
dreaptă va fi inclusă în planul
vab și același lucru îl vom face
și pentru planul abc vom duce o
dreaptă perpendiculară pe AB și
inclusă în acest plan abc și de
vreme ce vorbim de o piramidă triunghiulară
regulată adică triunghiul bazei
este echilateral triunghiul vab
este isoscel atunci cel mai simplu
este să alegem mijlocul segmentului
AB de și trec aici e mijlocul segmentului
AB atunci ce reprezintă v m v ă
m este mediană în triunghiul abe
Dar pentru că triunghiul este isoscel
de bază ab înseamnă că vm este
chiar înălțime în acest triunghi
Deci avem aici un unghi de 90 de
grade bun Ce reprezintă cm Păi
ce îmi este mediană în triunghiul
ABC cu triunghiul echilateral înseamnă
că cm este și înălțime Păi ce am
obținut am construit acele perpendiculare
inclusă în cele două plane perpendicularele
sunt pe dreapta ab în același punct
dacă unghiul plan al diedrului
este unghiul v m c și atunci Haideți
să notăm ca să facem o rezolvare
riguroasă Deci triunghiul abe sau
mai bine zis să începem așa cu
construcția noastră Deci construim
punctul m astfel încât a m segmentul
a m e congruent cu segmentul MB
Nu e neapărat să trecem congruență
de segmente putem să trecem și
egalitate de lungimi de segmente
construim punctul m astfel încât
m se află la mijlocul distanței
între a și b acum triunghiul vab
este un triunghi isoscel cu baza
BC M pardon cu baza ab știind că
BM este mediană Ce rezultă că vm
este și înălțime vm perpendicular
pe AB bun triunghiul ABC același
lucru vomota și pentru triunghiul
ABC care atenție este un triunghi
echilateral si m este mediană atunci
co să rezulte că ce e m este și
înălțime de cm este perpendiculară
tot pe AB și acum am obținut vm
și cm perpendiculare pe AB putem
să notăm că planele V a b și a
b c se intersectează după dreapta
ab dacă vrem să fim chiar riguroși
scriem și că vm este inclusă în
planul V a b și c m este inclusă
în planul bazei adică a b c din
toate aceste câte sunt câte relații
avem unul doi trei patru cinci
din toate aceste cinci relații
Ce rezultă o să scriu aici rezultă
că măsura unghiului format de planele
vab Deci acest plan planul V a
b cu planul ABC este de fapt egal
cu măsura unghiului făcut de dreptele
BM și cm cu alte cuvinte ce unghii
avem ce obținem avem unghiul măsura
unghiului Ia să vedem ce adică
acest unghi Sau dacă vreți unghiul
v m o pentru că punctele c o și
m sunt coliniare Deci acest unghi
avem vm si care e același cu unghiul
v m o cu alte cuvinte putem să
scriem că avem aici 30 de grade
toate datele sunt trecute pe figură
Haideți atunci să ștergem tot ce
am notat aici Și atunci să găsim
acum aria laterală Care e formula
aria laterală este egală cu produsul
dintre perimetrul bazei ori apotema
piramidei supra doi Deci avem nevoie
de perimetrul bazei adică lungimea
muchiei bazei și de apotema piramidei
care ia dă este reprezentat aici
dvm Păi ce să aflăm foarte simplu
putem să aflăm apotema piramidei
pentru că triunghiul v om Ce fel
de triunghi este este un triunghi
dreptunghic în o avem aici 90 de
grade și atunci Haideți să notăm
triunghiul v om este dreptunghic
în o triunghiul v o m măsura unghiului
o are 90 de grade și ce putem să
facem ca să determinăm lungimea
ipotenuzei Păi fie aplicăm o formula
sinusului Care este cateta opusă
adică vreo pe care o cunoaștem
supra ipotenuză Sau dacă vreți
putem să aplicăm teoremă unghiului
de 30 de grade Haide să aplicăm
teoremă unghiului de 30 de grade
care ne spune că într un triunghi
dreptunghi cateta opusă unghiului
de 30 de grade are lungimea egală
cu jumătate din lungimea ipotenuzei
Deci un v o este egală cu lungimea
ipotenuzei v m supra doi de unde
rezultă că vo Care este 4 egal
cu z m supra 2 înseamnă că obținem
că bem chiar să facem în așa fel
încât să ne încadrăm între un singur
rând Deci vom obține că vm are
patru ori 2 8 cm și atunci vom
șterge aici și deja scrie încă
avem 8 cm bun cum determinăm acum
lungimea muchiei bazei adică a
bad exemplu Păi ca să determinăm
lungimea muchiei bazei vom găsi
mai întâi Cât este apotema bazei
om după ce am găsit Cât este om
îl găsim foarte ușor pe cm și cm
este înălțime în triunghiul a b
c și știind că există o formulă
care leagă înălțimea în triunghi
echilateral de latura triunghiului
echilateral Deci mai întâi Vrem
să aflăm Cât este om foarte simplu
fie aplicăm Pitagora În triunghiul
vom da sau putem să aplicăm formula
cosinusului cosinus de m Haideți
să facem astfel să aplicăm formula
cosinusului Deci în același triunghi
cosinus de unghiul m este egal
cu ce vom obține trecem raportul
cateta alăturată unghiului m adică
om supra ipotenuză v e rezultă
că Haideți să scriem aici că avem
un v m rezultă că cosinus de 30
de grade va fi egal cu om pe care
vrem să îl aflăm supraveghem care
are 8 cm Cât este cosinus de 30
de grade avem radical din 3 supra
2 egal cu om supra 8 cât ne rezultat
unci că este om trecem aici o m
este egal cu avem 8 radical din
3 supra 2 10 obținem patru radical
din trei și dacă o să reușim să
scriem aici Deci patru să trecem
cu alb patru ori radical din 3
Atât este om acum dacă știm pe
de rost forum la care leagă apotema
bazei întru asemenea piramidă de
muchia bazei fie dacă nu ne bazăm
pe asemenea formulă atunci o deducem
personal prefer să deduc ca să
nu fiu nevoită să rețin prea multe
formule așa că știu că apotema
bazei adică om are 4 radical din
3 cm Ce legătură este între om
și cm o este centrul de greutate
al triunghiului ABC C M este mediană
asta înseamnă că om acest segment
are lungimea egală cu o treime
din lungimea medianei adică cm
supra 3 și rezultă de aici că cm
Cu cât este egală cu 3 ori om 3
înmulțit cu o m adică avem trei
înmulțiri cu 1000 este 4 radical
din 3 De ce obținem 12 radical
din 3 cm bun atât este însă cm
mai este înălțime Iată În triunghiul
abc cm înălțime În triunghiul abc
care Ce fel de triunghi este este
un triunghi echilateral o să scriu
așa liniuță echilateral atunci
rezultă că noi știm deja formula
pentru înălțimea în triunghi echilateral
și anume Deci avem aici m Dacă
trecem dacă notăm latura triunghiului
ABC cu l mic avem l mic radical
din 3 supra 2 vom obține din aceste
două relații altă pe de o parte
știind că cm este chiar o să subliniez
ce este 12 la de cal din 3 cm și
Pe de altă parte cm este el radical
din 3 pe 2 rezultă că e l mic radical
din 3 supra 2 ce avem aici este
egală cu 12 radical din 3 simplificăm
pe radical din 3 cu radical din
3 ca și cum am împărțit această
egalitate la radical din trei deci
rezultă că el supra 2 ne dă 12
adică el este egal cu 24 de cm
venim aici putem să ștergem trecem
direct că avem 24 de cm în acest
moment avem tot ce ne trebuie ca
să calculăm aria laterală totală
și volumul Deci o să ștergem tot
ce am notat aici în afară de formula
pentru aria laterală și venim și
calculăm aria la era ala este egală
cu perimetrul bazei Păi avem 24
ori 3 înmulțit cu apotema piramidei
Care este 8 supra doi și avem aici
putem să simplificăm prin doi ne
rămâne unul și patru patru ori
3 12 ori 24 ne de 288 cm pătrați
aria totală este egală cu aria
laterală plus aria bazei aria totală
a tunci este egală cu avem 288
plus aria bazei Latura este de
24 Avem așa 24 sau chiar o să scriu
aici aria bazei ne dă 24 la a doua
radical din 3 supra 4 de unde vom
obține aici Dacă simplificăm 124
cu 4 o să ne rămână 6 ori 24 ore
Adi cal din trei deci 144 radical
din 3 centimetri pătrați și adunăm
aici plus 144 radical din 3 de
fapt putem să dăm factor comun
aici pe 144 pe lângă 2 plus radical
din 3 tem să trecem așa între o
paranteză pătrată ca să scriem
aici centimetri pătrați volumul
este egal cu aria bazei ori înălțimea
supra 3 rezultă că volumul Nevada
avem aria bazei 144 ori radical
din 3 înmulțit cu înălțimea Care
este 4 supra 3 simplificăm aici
pe 144 cu 3 vom obține 1 144 împărțit
la 3 48 și vom avea 48 ori 4 192
radical din 3 cm cubi