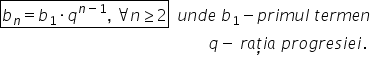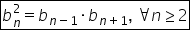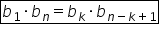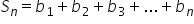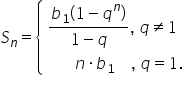Proprietațiile progresiei geometrice (teorie)

Salut discutăm în lecția aceasta

despre proprietățile progresiei

geometrice avem această progresie

geometrică notată cu B1 B2 bn am

notat rația progresiei geometrice

cu q unde m q este număr real diferit

de 0 iar în partea dreaptă am scris

un exemplu de progresie geometrică

ce a fost prezentat și în lecția

trecută spuneam atunci că dacă

un elev se înscrie pe saitul lecții

virtuale apoi a doua zi recomandă

saitul altor doi elevi apoi fiecare

dintre aceștia recomandă mai departe

saitul altor două persoane continuând

la acest mod se va ajunge la șirul

de forma 1 2 4 8 16 32 și așa mai

departe Aceasta este o progresie

geometrica cu rația egală cu doi

am fi putut să scriem acest șir

și cu ajutorul puterilor lui 2

astfel avem 2 la 0 2 la 1 a 2 la

a doua 2 la a treia și așa mai

departe pentru început ne propunem

să găsim formula termenului general

al unei progresii geometrice primul

termen al progresiei este B1 al

doilea termen se obține Înmulțind

primul termen cu rația al treilea

termen b 3 se obține Înmulțind

al doilea termen cu rația q egal

mai departe B2 este B1 nori q ori

q egal cu b 1 ori q la pătrat b

4 este egal cu b trei ori q și

egal mai departe cu B1 ori q la

pătrat ori q egal cu b 1 ori q

la puterea a treia așa mai departe

bn Haide să ne uităm puțin la acești

indici observăm că în formula lui

B2 avem q la puterea întâia în

formula termenului b3 avem fiu

la puterea a doua în formula termenului

B4 avem q la puterea a treia Așadar

bn va fi egal cu b 1 ori q la puterea

n minus 1 aceasta va fi formula

termenului general al unei progresii

geometrice în care se cunoaște

primul termen B1 și rația q punem

Așadar că o progresie geometrică

este bine determinată dacă se cunosc

primul termen și rația demonstrația

aceste formule se face prin inducție

matematică și exercițiu acum să

revenim la acest exemplu și Haideți

să calculăm al 15-lea termen al

acestui șir în cazul acestui șir

primul termen b 1 este egal cu

1 rația este egală cu 2 pentru

a vedea Câți elevi se scrie pe

Skype în a 15-a zi trebuie să facă

coulomb termenul de rang 15 Așadar

b15 va fi egal cu b 1 adică 1 ori

rația 2 la puterea 15 minus 1 egal

cu 2 la puterea a 14 Putem să lăsăm

rezultatul sub această formă dar

pentru simpla mea curiozitate o

să calculez 2 la puterea a 14-a

Iată 16.384 egal cu 16.384 prin

urmare în a 15-a zi se scrie 16.384

de elevi dacă acesta algoritmi

sar continua în continuare trecem

la o altă proprietate a progresiilor

geometrice să ne uităm puțin la

acest exemplu mai exact la primii

trei termeni ai acestei progresii

observăm că termenul din mijloc

2 la puterea a doua este egal cu

1 ori 4 apoi dacă ne uităm la următorii

trei termeni 2 4 și 8 observăm

că 4 la puterea a doua este egal

cu 2 ori 8 pentru că ea 16 este

egal cu 16 apoi 8 la puterea a

doua este egal cu 4 ori 16 64 egal

cu 64 observăm Așadar pentru o

progresie geometrică pătratul fiecărui

termen începând cu al doilea este

egal cu produsul termenilor Alăturați

în cazul general Acest lucru se

va scrie astfel de n la pătrat

este egal cu b n minus 1 ori b

n plus 1 Așadar pătratelor cărui

termen începând cu al doilea va

fi egal cu produsul vecinilor săi

demonstrăm această formulă nu știm

că no ce progresie geometrică Raportul

a doi termeni consecutivi este

constant așa dar raportul b n supra

b n minus 1 este egal cu q din

această relație Exprimă în pe bn

acesta va fi egal cu b m minus

1 ori q de asemenea raportul b

n plus 1 supra bn va fi egal cu

q pentru că și Aceștia sunt doi

termeni consecutivi din această

relație exprimăm bn acesta va fi

egal cu b n plus 1 supra q acum

înmulțim aceste două relații membru

cu membru Bn Bn este egal cu bn

la pătrat egal cu bn minus 1 ori

q ori b n plus 1 supra q se simplifică

q și obținem de 1 ori b n plus

1 Iată așadar am arătat că bn la

pătrat este egal cu b n minus 1

ori b n plus 1 să reținem și această

formulă dacă avem trei termeni

consecutivi între o progresie geometrică

atunci pătratul termenului din

mijloc este egal cu produsul vecinilor

săi să continuăm cu altă proprietate

geometrice mai întâi ne uităm la

acest exemplu observăm că unul

ori 32 este egal cu 2 ori 16 și

egal cu 4 ori 8 putem să și scrie

ma chest lucru unor 32 egal cu

216 egal cu 4 ori 8 observăm Așadar

pentru o progresie geometrică produsul

termenilor extremi este egal cu

produsul termenilor egal depărtați

de termenii extremi în cazul general

Acest lucru se va scrie astfel

B1 ori b n este egal cu b 2 ori

b minus 1 egal așa mai departe

cu BK ori b minus k plus unu dacă

BK este el caulea termin pornind

de la stânga spre dreapta atunci

el Calea termen de la dreapta spre

stânga este b indice n minus k

plus unu observăm că întotdeauna

suma indicilor trebuie să fie egală

cu n plus unu așa dar el caulea

termen de la dreapta spre stânga

este b n minus k plus unu ca să

respectăm această regulă și anume

suma indicilor să fie egală cu

n plus 1 demonstrăm această relație

Moon calcula produsul BK ori b

minus c plus 1 Haideți să ne reamintim

formula termenului general al unei

progresii geometrice bn este egal

cu B1 ori q la puterea n minus

1 și aplicăm această formulă aici

bac la Apa va fi egal cu b 1 ori

q la puterea k minus 1 ori b minus

k plus 1 este B1 ori q la puterea

n minus k plus 1 minus 1 rămâne

în minus k egal cu b 1 ori b 1-q

la puterea aici adunăm exponenții

și obțin mq la puterea n minus

1 egal observăm că B1 ori q la

n minus 1 este bn conform acestei

formule și obținem în final egal

cu b 1 ori b n iar de unde am pornit

BK ori b minus k plus 1 este egal

cu b 1 ori bn așa dar am demonstrat

aceasta egalitate între o progresie

geometrică produsul numerelor extrem

este egal cu produsul numerelor

egal depărtate de numerele Extreme

și ultima proprietate a progresiei

geometrice ne propunem să deducem

o formulă de calcul pentru suma

primilor n termeni ai unei progresii

geometrice întâlnim două situații

posibile dacă rația este egală

cu 1 atunci primul termen al progresiei

este B1 al doilea termen este B1

ori 1 Așadar b-2 este egal cu b

1 al treilea termen va fi și acesta

egal cu b doi de c egal și cu B1

și așa mai departe cu alte cuvinte

între o progresie geometrică în

care rația este egală cu unu toți

termenii sunt egali cu primul termen

prin urmare suma primilor n termeni

ai unei progresii geometrice is

an a fi egală cu n ori B1 pentru

că avem n astfel de termeni toți

egali cu B1 acum să vedem ce se

întâmplă dacă rația este diferită

de 1 să calculăm suma primilor

n termeni aceasta va fi egală cu

B1 plus de doi plus b 3 și așa

mai departe voi scrie și penultimul

termen b n minus 1 plus b n Haide

să înmulțim această relație cu

q obținem q s n egal cu b 1-q plus

b 2 q plus b 3 plus așa mai departe

plus b minus 1 plus b n ori q acum

scădem cele două relații membru

cu membru și obține m s n minus

Q s n egal acum observăm că în

membrul Drept au loc niște reduceri

de termeni pentru că Iată de 2

este egal cu b uneori q b3s tei

egal cu b 2 ori q bn este egal

cu bn minus 1 ori Q în momentul

ala care scădem aceste două relații

membru cu membru se reduc acești

termeni b3 cu b 2 q se va reduce

și b3 q cu termenul de mai sus

la fel și bem minus 1 iar bn se

reduce cu b n minus 1-q și în final

ne mai rămâne primul termen b-1

și ultimul acesta b n o q acum

da factor comun pe sn avem Aston

pe lângă 1 minus q egal cu b 1

minus pe bn o să îl scriem B1 ori

q la A minus unu Am aplicat formula

termenului general Și mai avem

ori q egal cu b 1 minus b 1 ori

q adunăm exponenții obținem q la

an în continuare de faptul comun

pe B1 și avem b 1 pe lângă 1 minus

Q la n și acum din aceasta egalitate

o să le exprimăm pe ethan este

în va fi egal cu b 1 pe lângă 1

minus Q la puterea n supra 1 minus

Q aceasta va fi formula de calcul

pentru suma primilor n termeni

ai unei progresii geometrice dacă

dorim Putem să scriem această formulă

și alt fel de 1 pe lângă q la n

minus 1 supra q minus 1 și acum

să revenim puțin la acest exemplu

în cazul în care ne interesează

Câte persoane sar înscriere pe

saitul lecții virtuale în total

în cele 15 zile trebuie să calculăm

suma primilor 15 termeni așa cum

am mai spus primul termen b-1 al

progresiei este 1 rația progresiei

este egală cu 2 și atunci Haide

să calculăm suma primilor 15 termeni

is 15 aplicăm această formulă B1

este 1 pe lângă 1 minus rația este

doi Deci avem doi la puterea 15-a

supra 1 minus 2 egal cu 1 minus

2 la puterea a 15-a supra minus

1 și egal cu 2 la a 15-a minus

1 Am putea să lăsăm rezultatul

sub această formă așa dar voi în

exerciții în care aveți puteri

foarte mari nu trebuie să faceți

calculele finale eu o să calculez

totuși 2 la puterea 15-a doi la

15-a Iată 32768 de elevi 32768

minus 1 și obținem 32767 de elevi

și acum Haideți să ne reamintim

pe scurt principalele proprietăți

ale progresiilor geometrice Iată

prima formulă este formula termenului

general al unei progresii geometrice

bn este egal cu B1 ori q la puterea

n minus 1 o altă proprietate importantă

în cazul în care avem trei termeni

consecutivi ai unei progresii geometrice

pătratul numărului din mijloc este

egal cu produsul numerelor alăturate

apoi o altă proprietate importantă

în orice progresie geometrică produsul

numerelor Extreme B1 ori b n este

egal cu produsul numerelor egal

depărtate de numerele Extreme iar

pentru a calcula suma primilor

n termeni ai unei progresii geometrice

Avem două posibilități în cazul

în care rația este diferită de

1 formula de calcul va fi b 1 pe

lângă 1 minus scriu la n supra

1 minus Q iar în cazul în care

rația este egală cu 1 suma primilor

n termeni să fie egală cu n ori

b 1 am atât Pa