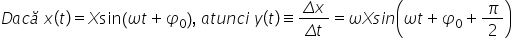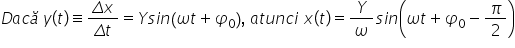Proprietăţile funcţiilor sinusoidale.

în cea de a 6-a lecție de curent

alternativ vom discuta despre proprietăți

ale funcțiilor sinusoidale și despre

implicațiile acestor proprietăți

pentru proprietățile curentului

electric alternativ prima proprietate

foarte importantă a funcțiilor

sinusoidale din punct de vedere

al curentului alternativ este aceea

Că variat viteza de variație a

unei funcții sinusoidale e tot

o funcție sunt sinusoidală cu aceeași

pulsație dar defazată înainte cu

piep 2 radiani adică cu 90 de grade

și cu amplitudinea y no tată cu

y egal cu produsul dintre pulsație

funcției sinusoidale și amplitudinea

primei funcții sinusoidale Haideți

să scriem ecuația și să explicăm

ca și comentariu la toate aceste

ecuații și demonstrațiile lor sunt

Oare cum complicate dar ideea de

bază este foarte simplă și important

pentru dumneavoastră este să rețineți

ideea de bază a aceste proprietăți

Deci ce spune această teoremă dacă

vreți dacă avem o anumită funcție

sinusoidală x de Tedi și x este

valoarea momentan sau instantanee

la moment dat m Care este egală

cu altitudine x mare muncită cu

sinus de omega-3 plus fizzer aceasta

este Forma generală a unei funcții

sinusoidale apare în modelul matematic

al curentului alternativ această

teoremă spune că dacă x de tei

este are această formă atunci y

de te care prin definiție este

viteza de variație a lui x din

Delta XP Delta t variația lui x

în unitatea de timp are această

formă adică este și el ydp-143

pulsația Omega și magnitudinea

x a lui x de 3 lysi Omega x iar

argumentul lui funcții sinus în

cazul lui y ritm este același ca

în cel pentru funcția x Deci omega-3

plus fie zero plus unde faza și

constant de pi pe 2 radiani adică

90 de grade asta înseamnă că y

de te întreb prezentare fazorială

va fi perpendicular pe de pe veți

vedea în lecțiile viitoare De ce

această proprietate este foarte

utilă pentru că putem calcula din

ea viața unui curent sau variațiuni

tensiuni Deci pornim cu anumită

funcție sinusoidală a tensiunii

sau curentului alternativ de cheeks

de TVA fără tensiune curent alternativ

și folosind această proprietate

putem scrie direct Care este viteza

de variație a curentului sau tensiune

este Haideți să demonstrăm această

proprietate Deci vrem să calculăm

1 Delta x unde x are această formă

Delta x prin definiție este valoarea

lui x la un timp ulterior deci

te plus Delta t aceasta este diferența

de timp Delta t minus valoarea

lui la momentul nici eu si Asta

este definiția variației lui x

în interval de el tot a și pur

și simplu înlocuim în aceste două

funcții x de 3 plus de alta Ateș

xdt din Definiția lui xdt Deci

obține încă Delta x este egal cu

amplitudinea x înmulțit cu sinus

de omega-3 plus delta teffi 0 minus

x ilis de omega-3 plus fizzer de

plus Delta t a apărut aici putem

Rescrie foarte simplu și veți vedea

imediat De ce această funcție ca

fiind x sinus de Omega Delta t

plus omega-3 plus fie zero De ce

am grupat acest argument în felul

acesta minus aceeași funcție xdt

apoi folosind următoarea proprietate

trigonometrică și anume că sinus

de Alfa plus Beta este egal cu

sinus de Alfa cosinus de Beta plus

cosinus de Alfa sinus de beton

Deci folosind această proprietate

trigonometrică desfacem acest sinus

Deci primul sinus desfacem în doi

termeni unde Alfa va fi Omega deltatech

și Beta va fi omega-3 plus fi 0

Deci folosim acea proprietate un

Alfa fiind această parte argumentului

și Battlefield această parte argumentului

și obținem această formulă aparent

complicată Deci x va fi Delta x

să fie x înmulțit cu sinus de Alfa

Dică Omega Delta t cosinus de B

tadi come gotti plus fie 0 și apoi

cel de aducerea doua parte cosinus

sinus cosinus de Alfa decomag adel

tot a înmulțit cu sinus omega-3

plus zero și na rămas acest ultim

termen pe care îl pur simplu scrie

mx-5 Înmulțind între întreaga ei

formulă trigonometrică acum o să

vină simplificarea ca are ca întotdeauna

după cum am văzut în lecțiile precedente

pornește de la ideea unghiurilor

mici sau de faza celor mici care

corespund unor intervale temporale

mici Deci dacă Delta fii Care este

Omega Delta t tinde la 0 Adică

are o valoare mică atunci putem

scrie urmele formule aproximativ

sinus de sinus de un unghi mic

este aproximativ egal cu unghiul

adică sinus de Omega de el tot

este aproximativ egale cu Omega

de al tatei iar cosinus de unghi

mic este aproximativ egale cu 1

Deci cosinus de Omega Delta t este

aproximativ egale cu unu această

parte este această aproximație

este evidentă pentru cosinus de

0 este 1 Deci cosinus de Alfa unde

Alfa se apropie de zero este un

această aproximație este mai puțin

evidentă totuși și ea este adevărată

bineînțeles și pur și simplu înlocuim

acestea aproximație în relația

de Sus în formula de sus Deci acest

termen va deveni Omega Delta ten

acest termen va deveni unul și

imediat observăm că dacă acest

termen este unul atunci al doilea

termen din din această paranteză

pătrată se va simplifica cu al

treilea De ce acesta se va simplifica

cu acesta rămânem numai cu primul

termen Deci Delta x este egal cu

Omega x Delta t cosinus de omega-3

plus fie 0 și de aici putem scrie

că Delta x este egal cu Omega x

Delta test sinus de omega-3 plus

și zero plus pai pe 2 unde am folosit

faptul că cosinus identitatea trigonometrică

că cosinus de Alfa este sinus de

Alfa plus 90 de grade adică pi

pe 2 radiani și aceasta este exact

relația pe care am dorit o pentru

că dacă împărțim Delta xSlayder

tate pentru a obține migreze de

variație a lui x vom obține exact

Omega x sinus de omega-3 plus și

0 plus 2 ca și comentariu Această

fază acest defazaj pe care viteza

de variație primește în plus față

de x Deci din bule de real unghiurilor

ydp-163 plus 90 de grade față de

aceasta Reprezintă un interval

temporal după cum am discutat în

lecția trecută deci Delta fii pipă

2 implică un Delta t între yigal

cu un sfert de perioadă tp4 în

DT este perioada funcției sinusoidale

ca și observații iarăși foarte

importantă această implicație Deci

această teoremă care are acest

sens al demonstrație de fapt o

echivalență în sensul că putem

pleca de la un Y5 obține forma

pentru Deci mai exact dacă avem

dacă cunoaștem invers cunoaștem

viteza de variație între o problemă

și ea are forma Asta e y e sinus

de omega-3 plus și 0 atunci parametrul

x are următoarea valoare Y8 la

pulsația omega înmulțit cu sinus

de Omega plus fie 0 minus fie pe

doi deci putem aborda și problema

în sens opus nu aștept invers viteza

de variație y și dorim să aflăm

Care este funcția sintactică DT

și atunci Aceasta este implicația

o dăm fără demonstrație dar îi

dea trebuie reținută Deci dacă

cunoaștem ele te și el are o astfel

de forme atunci x de TVA avea forma

aceasta amplitudinea va fi amplitudinea

învăța pulsație argumentului sinus

va fi același cu excepția unei

unei defazaj live Deci minus 90

de grade xdt va fi bineînțeles

Dacă y este în față cu 90 de grade

față de x atunci x va fi în spate

față de e y scrisă matematică Asta

înseamnă următorul lucru că dacă

avem după cum însuși două funcții

sinusoidale X1 DT cu această formă

și X2 de te cu această formă Deci

forma cea mai generală a două funcții

sinusoidale pe care le întâlnim

în cazul modelului matematic pentru

curentul alternativ bineînțeles

atunci de tecar este suma celor

doi va avea forma x oceans de omega-3

plus fie 0 Deci are tot o funcție

sensului de ala tot pulsația termenul

dependent de timp al argumentului

al fazei este Omega te și va avea

o anumită amplitudine și un anumit

de fază aș fi 0 care sunt legate

de X1 X2 și fie zero unu și zero

doi putem și în manualul dumneavoastră

se aplică tot felul de identități

la trigonometrice pentru a demonstra

această teoremă și în particular

pentru a găsi valorile lui x și

zero în funcție de Deci x se poate

calcula și se obține un o valoare

de pandantive X1 X2 fi 0 1 și 0

2 și la fel și 0 se poate calcula

și se obține o formulă a lui frizerul

în funcție de aceeași parametri

cunoscuți sau dați X1 X2 fie zero

unu și zero doi această demonstrație

nu este una foarte simplă în special

dacă Considerăm că X1 este diferit

de X2 adică cele două funcții sinusoidale

au atitudini diferite totuși Se

poate rezolva și o Găsiți în manual

interesant De comentat De ce o

să iau o direcție un pic diferită

este că dacă folosind diagrama

fazorială pentru X1 X2 pentru a

afla pe x de te soluția sau demonstrație

de vine semnificativ mai simplă

Deci Să considerăm diagrama fazorială

în care pe care am explicat în

lecția trecută în care avem acești

doi fazori X1 și X2 reamintesc

valorile instantanee Deci suna

mix de T și x 2m x de ten vor fi

proiecțiile pe axa y si Haideți

să folosim acești vectori pentru

a calcula Spre exemplu fizzer Deci

Bineînțeles că vectorial vorbind

x este egal cu x 1 plus x 2 fazorul

total x care DEX de ten Vichy xdt

va fi proiecția pe igrec acesta

este valoarea momentană Deci xdt

e deschis de acest fel doar cu

roșu și el este suma vectorială

a lui X1 și X2 X1 și X2 dacă scriem

relații dintre proiecții Deci proiectăm

această ecuație vectorială pe axa

o x 0 nicicând proiectăm pe axa

o x 0 obținem că x cosinus de fi

01 scuzați de fie zero este egal

cu x 1 cosinus de 0 1 plus x 2

cosinus ep02 deci pur și simplu

am spus că proiecția lui x pe axa

o x 0 este egală cu suma proiecțiilor

X1 și X2 pe axa o x 0 Deci x cosinus

de fi 0 egal cu x 1 cosinus de

fi 0 1 plus x 2 cosinus de fi 0

la fel dacă proiectăm ecuația vectorială

pe axa o y 0 obținem că x sinus

deși 0 este egal cu x 1 sinus de

0 1 plus x 2 sinus de pi zero doi

și avem Două ecuații cu două necunoscute

am și anume x și fizzer observăm

că ecuația pentru fi 0 rezultă

imediat Dacă împărțim a doua ecuații

la prima ecuații x se simplifică

și obținem ecuația pentru fi 0

care spune că tangentă de fie zero

adică sinus învăț la cosinus va

fi egal cu raportul dintre aceste

două cantități Deci vedeți Spre

exemplu si simplu putem obține

Cât de imediat putem obține folosind

diagrama fazorială ecuația pentru

fizzer la fel apoi după ce știm

fie zero putem introduce în întruna

din ecuații și obțin ecuația pentru