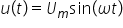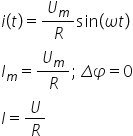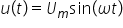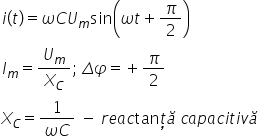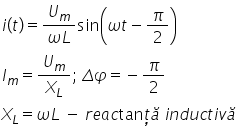Rezistorul, bobina şi condensatorul în curent alternativ.
Tag-uri
Partajeaza in Google Classroom

Transcript
în cele 7 lecție de curent alternativ
vom discuta despre proprietățile
elementelor principale de circuit
rezistorul bobina și condensatorul
pentru a studia proprietățile rezistorului
Să considerăm un rezistor conectat
la o sursă de curent alternativ
și Deci vom avea o intensitate
alternativă prin deal dacă forma
tensiunii alternative ei este aceasta
adică ude te valoarea momentană
este valoare maximă munții cu ținute
omega-3 dorim să stabilim Care
este forma intensității valorii
momentane a intensității în acest
tip de circuit legea 1000 valabilă
și pentru mărimile momentane ale
curentului alternativ pentru că
la un moment dat te bineînțeles
cu valoarea momentan este o constantă
ieri fixă la cel mai mint ati prin
definiție și la fel și intensitate
deci putem scrie că valoarea la
un moment dat a a intensității
este egală cu valoarea la momentul
respectiv a tensiunii împărțită
la rezistența Care este bineînțeles
independentă de timp și deci putem
scrie această relație foarte simplă
de legătură între intensitate și
tensiune de unde rezultă următoarele
concluzii importante prima este
că raportul dintre valorile maxime
ale intensității și tensiunii respectă
legea om de cm egal cu u m împărțit
la R de asemeni nu există niciun
defazaj între valorile momentane
ale intensității și tensiunii reamintesc
un defazaj adică nu unghii dacă
vreți in termeni de fazori ar fi
apărut ca un termen constant independent
de timp în argumentul funcției
ce nu avem un astfel de termen
în cazul rezistorului asta înseamnă
că intensitatea și tensiunea printr
un rezistor Sunt în față adică
acestor termeni independent de
timp este nul În diagrama fazorială
asta înseamnă că fasolii intensității
și tensiunii prin rezistor sunt
coliniari și se mișcă împreună
cu omega-3 bineînțeles valorile
momentane ale intensității și tensiunii
sunt proiecțiile pe axa e rect
de cerceta va fi de ten și acesta
va fi cu DT de asemeni după cum
vă reamintiți am definit intensitățile
și tensiune afective și ele au
ecuația simpliq simplă Spre exemplu
pentru intensitate intensitatea
efectivă este m împărțit la radical
din 2 la fel și un cu efectiv este
egal cu u m împărțit la radical
din 2 rezultă Deci că putem scrie
legea om și pentru valorile efective
ale curentului alternativ pentru
tensiune și intensitate rezistorul
se opune trecerii curentului independent
de pulsație acestuia de chiar nu
depinde de Omega ceea ce înseamnă
că în prun grafic aer de Omega
El este o constantă pulsații vom
vedea că acest lucru se schimbă
pentru celelalte două elemente
de circuit să trecem la condensator
Deci Considerăm același tip de
circuit un condensator legat direct
la o sursă de tensiune alternativă
la fel udt valoarea momentană a
tensiunii va avea aceeași formă
și Încercăm să stabilim în acest
în acest caz pentru condensator
valoarea sau formula pentru intensitatea
momentană la curent lui pornind
de la ecuația capacității condensatorului
care prin definiție este raportul
dintre sarcină pe armături vă aduc
aminte că un condensator are sarcini
egale și de semn opus pe cele două
plăci sau pe cele două armături
Deci vom avea acesta este Deci
plus și minus Q și folosind formula
pentru valoarea momentană a tensiunii
rezultă că ciudate valoarea momentană
a sarcinii pe condensator este
ce ori o detin definiția intensității
Care este variația sau viteza de
variație a sarcinii un conductor
putem obține că identi este Omega
c u m înmulțit cu sinus de omega-3
plus pai pe doi cum am ajuns la
această relație am folosit teorema
demonstrată în lecția precedentă
dacă revedeti lecția precedentă
am stabilit acolo că dacă o funcție
sinusoidală pentru o funcție sinusoidală
variația temporală este tot o funcție
sinusoidală pentru care amplitudinea
sau valoarea maximă este mulți
tăcu pulsația și argumentul funcție
sinusoidale Este defazat cu plus
pi pe 2 deci dacă q de t are această
formă sinusoidală atunci Delta
cupe Delta t Care este intensitatea
curentului va avea această formă
vă rog să le vedeți în lecția trecută
teorema care leagă o funcție sinusoidală
de variație e temporală de aici
putem scoate următoarele proprietăți
importante md5 valoarea maximă
a intensității curentului este
poate fi scrisă ca raportul dintre
om și un parametru pe care notăm
cu X cm unde x si prin definiție
va fi unul pe Omega C de joacă
Înlocuiți vedeți Că întradevăr
e m adică această mărime va fi
egală cu omega.com după cum am
găsit și de asemeni putem Extrage
din această formulăm defazajul
dintre intensitatea curentului
și tensiunea curentului pentru
un condensator și observăm că intensitatea
curentului este defazată înaintea
tensiunii cu piper 2 radiani adică
90 de grade Deci inși us în defazate
în cazu condensatorului în sensul
că intensitatea curentului va fi
în față sau dorul ei va fi de fazat
în față cu 90 de grade bineînțeles
u m adică fazorul tensiunii se
rotește cu omega-3 și Deci și e
m se va roti cu omega-3 pentru
că el se află la 90 de grade un
unghi de 90 de grade constant față
de om acest parametru XC se numește
reactanța capacitivă el se opune
trecerii curentului dar o face
întrun mod invers proporțional
cu pulsații acestuia Bineînțeles
dacă Reprezentăm x si ca funcție
de Omega din Definiția lui obținem
că el scade este invers proporțional
cu pulsația curentul continuu Deci
cazul curentului continuu dacă
vreți este un caz particular pentru
pulsație 0 atunci obținem că x
si y este infinit 1 supra 0 este
infinit și atunci curentul prin
condensator este zero ceea ce înseamnă
că în regim de curent continuu
condensatorul se manifestă sau
se comportă ca un întrerupător
deținută ciucure împlinea continuu
să trecem la bobina Considerăm
la fel o bobină conectată la o
sursă de curent alternativ a cărei
tensiune valoare momentană a tensiunii
are această formă un ținut două
negativ ca și în celelalte două
cazuri și la fel Încercăm să stabilim
legătura dintre această valoare
momentană a tensiunii și valoarea
momentană intensității curentului
prin bobina pornind de la ecuația
pentru tensiunea electromotoare
indusă în bobina dar ce avem un
curent inductor ce trece prin bobină
din legea Faraday putem scrie această
formulă în care am folosit pentru
fluxul hindus relația simplă el
ori și de ce aceasta este legea
afara de pentru un flux egal cu
eroi atunci putem scrie că Delta
e este egal cu împărțit la al ei
Este exact această tensiune care
induce curentul A deci Delta este
egal cu u m împărțit la al sinus
de omega-3 iar își din lecția trecută
în care am dat câteva teoreme ale
proprietăților funcțiilor sinusoidale
am dat o teoremă Celica variația
temporală a unei funcții sinusoidale
de funcție în sine și atunci spuneam
că dacă variația unei funcții în
timp este o funcție sinusoidală
atunci funcția în sine va avea
o amplitudine împărțită la pulsația
omega și un argument defazat în
spate cu pi pe 2 Deci vă rog să
revedeți din nou lecția precedent
din acea teoremă putem de duce
forma lui ai de te De ce ai de
te din nou va avea amplitudinea
împărțită la pulsația omega iar
argumentul faza dacă vreți în cazul
fazori lor va fi defazat în spate
cu VIP 2 radiani adică cu 90 de
grade de aici din proprietățile
principale ale bobinei în circuit
alternativ și anume intensitatea
maximă care este bineînțeles această
mărime Deci identificăm această
mărime cu intensitatea maximă și
a este egală cu um împărțit la
Unix el motivul pentru care am
introdus atât XC cât și Axel este
pentru că am dorit să dăm o formă
a legăturii dintre a m și m în
ambele cazuri bobină și condensator
similară legii om Pentru că atunci
XC și Axel se vor comporta întrun
fel ca rezistența din legea om
Deci am definit în acest fel și
bineînțeles XL va fi Atunci scuzați
ar trebui să fie XL aici nu XC
Deci parametrul acesta este definiția
lui XL Deci XL este definit ca
Omega el din această formulă pentru
ai de te asemeni din această formulă
observăm că curentul este defazat
în spate față de tensiune cu piept
2 adică cu 90 de grade Deci dacă
facem schema sau diagrama fazorială
a bobinei în circuit de curent
alternativ obținem că curentul
este defazat cu 90 de grade în
spatele tensiunii va duc aminte
în cazul condensatorului era defazat
în față cu 90 de grade Deci invers
bineînțeles la fel de in se rotește
cu udăm fazorul tensiunii se rotește
cu Omega din această formulă și
bineînțeles atunci și e m sau fazorul
intensității se va roti și el tot
cu omega-3 Dar fiind tot timpul
în spate rămânând tot timpul în
spate cu un unghi constant de pi
pe 2 radiani sau 90 de grade reactanța
inductivă XL se opune trecerii
curentului direct proporțional
cu pulsația acestuia Deci dacă
Reprezentăm XL ca o funcție de
Omega obținem o formă un grafic
liniar Deci obținem această dependență
liniară Fanta care este tangenta
unghiului dintre grafic și axa
pulsatiei va fi felul în care se
opune trecerii curentului o bobină
este bineînțeles inducând un curent
care se opune curentul inductor
Deci va apărea înăuntru bobinei
un curent ai dus care se va opune
curentului inductor putem vedea
cum anume se comportă o bobină
în curent continuu punând condiția
tranziției de la curent alternativ
la curent continuu Care este pur
și simplu pulsație zea un curent
continuu este un curent alternativ
fără oscilații bineînțeles pulsația
este viteza de oscilație Deci dacă
nu avem o scila ții nu avem pulsație
curentul de vine continuu și atunci
în cazul bobinei obținem x l egal
cu 0 Deci dacă Omega iza.ro XL
va fi egal cu zero ceea ce implică
o intensitatea curentului Infinity
Deci intensitatea maxima sau m
Dacă vreți care va fi urăm împărțit
la omega el va fi egal cu zero
în concluzie în curent continuu
bobina îți se comportă ca un fir
pur și simplu Deci curentul continuu
va trece prin ea ca prin cont prin
tu un conductor normal