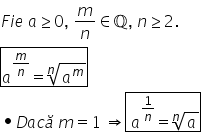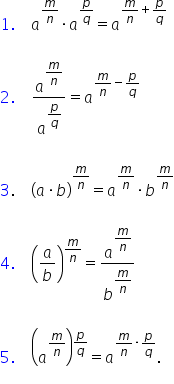Puteri cu exponent rațional

atunci când calculăm o putere cu

exponent natural de exemplu un

nou la a doua știind că trebuie

să înmulțim numărul 9 cu el însuși

de două ori iar rezultatul este

81 când avem o putere cu exponent

negativ lucrurile sunt destul de

simple pentru că trebuie doar să

inversăm această fracție și vom

scrie 1 supra 9 la pătrat Adică

1 supra 81 ce se întâmplă însă

când avem un exponent rațional

cum vom calcula 9 la 1 pe 2 pentru

a calcula valoarea lui x Haideți

mai întâi să ridicăm la pătrat

acest număr nou la 1 pe 2 ridicat

la a doua dacă am folosit proprietățile

puterilor pe care le cunoaștem

deja ar trebui să înmulțim exponenții

Deci am avea 9 la puterea doi pe

doi adică 9 la 1 Iași egal cu 9

Deci numărul 9 la 1 pe 2 este acel

număr care ridicat la pătrat ne

dă nouă Dar numărul care ridicat

la pătrat ne dă nouă este radical

din 9 așa dar putem să scriem că

9 la 1 pe 2 este egal cu radical

din 9 sau dacă vreți radical de

ordinul 2 din 9 dec iată că puterile

cu exponent rațional conduc la

radicali în cazul general Putem

să scriem următoarea relație a

la puterea 1 pe an va fi egal cu

radical de ordinul n din ei să

mai vedem câteva exemple șapte

la 1 pe 3 va fi egal cu radical

de ordinul 3 din 7 3 la puterea

1 pe 4 va fi egal cu radical de

ordinul 4 din 3 să reținem că întotdeauna

numitorul fracției devine indicele

radicalului cum vom calcula însă

minus 3 la puterea unu pe patru

dacă folosim această relație ar

trebui să avem radical de ordinul

4 din minus 3 însă nu putem extrage

un radical de ordin par din un

număr negativ în consecință pentru

că această formulă să fie corectă

trebuie să punem condiția ca numărul

ei să fie mai mare sau egal cu

0 Haideți o calculăm acum 3 la

puterea 5 supra 6 5 supra 6 se

poate scrie 1 pe 6 ori 5 Care va

fi egal cu 3 la 1 pe 6 totul la

a cincea adică radical de ordinul

6 din 3 ridicat la a cincea Care

este egal cu radical de ordinul

6 din 3 la a cincea în cazul general

această relație se va scrie astfel

A la puterea M supra n este egal

cu radical de ordinul n din a la

m unde a este un număr pozitiv

întotdeauna numitorul fracției

devine indicele radicalului să

vedem în continuare care sunt proprietățile

puterilor cu exponent rațional

să vedem ce se întâmplă atunci

când înmulțim două puteri cu aceeași

bază avem de exemplu a la m supra

n înmulțit cu a la P supra q probabil

a țintui deja că trebuie să adunăm

exponenții dar Haideți să demonstrăm

acest lucru bazin de nervi proprietățile

radicalilor m supra n este radical

de ordinul n din a la m iar al

apei supra q este radical de ordinul

q din ăla pe pentru a înmulțit

2 radical având ordine diferite

va trebui mai întâi sa aducem la

același ordin cel mai mic multiplu

comun al numerelor n și q este

produsul n q Deci mă mai avea radical

de ordinul n q din a la m q înmulțit

cu radical de ordinul n q din a

la n p egal Putem să scriem acum

sub un singur radical avem radical

de ordinul n q din a la mq înmulțit

cu a la n p final cu radical de

ordinul n q în continuare folosind

proprietățile puterilor cu exponent

întreg sub radical avem un produs

de două puteri cu aceeași bază

exponenții se adunăm vom avea a

la mq plus mp acum scriem acest

număr sub formă de putere cu exponent

rațional și vom avea a la puterea

mq plus n p supra n q egal cu ei

aici despărțim în două fracții

prima fracție va fi mq supra n

q iar a doua fracție va fi n p

supra n q egal aici simplificăm

cu q iar Aici simplificăm cu N

și obținem în final A la puterea

M supra n plus b supra q am demonstrat

așa doar că atunci când înmulțim

două puteri cu aceeași bază exponenții

se adună să vedem pe scurt care

ar fi celelalte proprietăți ale

puterilor cu exponent rațional

fără să le mai demonstrăm demonstrația

acestora se bazează pe proprietățile

radicalilor am arătat Așadar că

atunci când înmulțim două puteri

cu aceeași bază exponenții se adună

atunci când împărțim două puteri

cu aceeași bază exponenții se scad

următoarea proprietate care decum

un produs la o putere se ridică

fiecare Factor la acea putere atunci

când avem o fracție ridicată la

o putere se ridică atât numărătorul

cât și numitorul la acea putere

și ultima proprietate importantă

în ridicăm o putere la o altă putere

exponenții se înmulțesc să mai

vedem în continuare câteva exerciții

să calculăm de exemplu 27 la puterea

2 pe 3 va fi radical de ordinul

3 din 27 la a doua pentru a ușura

calculul vom scrie astfel radical

de ordinul 3 din 27 totul la pătrat

egal cu 3 la a doua adică 9 un

alt exercițiu să calculăm 25 la

puterea minus 1 pe 2 avem exponent

negativ Deci vom scrie 1 supra

25 la 1 pe 2 egal cu 1 supra radical

din 25 Adică 1 pe 5 Haideți să

calculăm acum radical din 7 înmulțit

cu radical de ordinul 3 din 7 știind

că pentru a înmulțit 2 radical

trebuie să aducem la același ordin

dar acum putem proceda și altfel

scrie în radicali sub forma unor

puteri cu exponent rațional radical

din 7 este 7 La 1 pe 2 Iar următorul

radical se poate scrie 7 la 1 pe

3 acum înmulțim două puteri cu

aceeași bază de ce adunăm exponenții

avem 7 la puterea 1 pe 2 plus 1

pe 3 egal cu 7 la 5 supra 6 aici

Am aplicat cu trei aicea ma pli

fiica cu 2 3 plus 2 5 pe 6 egal

în continuare cu radical de ordinul

6 din 7 la a cincea este foarte

important să rețineți că numitorul

fracției devine indicele radicalului

în continuare aș vrea să discutăm

câteva lucruri despre ordonarea

puterilor cu exponent rațional

dacă a este un număr pozitiv iar

Air 1 și r 2 două numere raționale

putem întâlnii următoarele două

situații prima situație în cazul

în care a este un număr mai mare

ca 1 iar R 1 este mai mic ca al

2 atunci se păstrează relația de

ordine dintre exponenți și în cazul

puterilor Deci ei la R1 va fi mai

mic decât a la r 2 și a doua situație

dacă a este un număr cuprins între

0 și 1 am spus că ei trebuie să

fie număr pozitiv Deci ei nu poate

să fie mai mic ca 0 iar R 1 este

mai mic ca r2 atunci În situația

aceasta relația de ordine se schimbă

Deci ala R1 va fi mai mare decât

a la r 2 de exemplu 2 la puterea

unu supra trei va fi mai mic decât

2 la puterea 2 supra 3 pentru că

1 pe 3 este mai mic decât 2 pe

3 iar baza este supraunitară însă

1 supra 2 ridicat la 1 pe 3 va

fi mai mare decât 1 pe 2 ridicat

la 2 pe 3 pentru că în acest caz

baza 1 pe 2 este subunitară