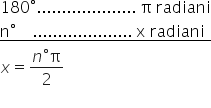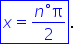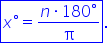Radiani și grade
Tag-uri
Partajeaza in Google Classroom
Transcript
salut în lecția aceasta discutăm
despre măsurarea unghiurilor în
grade și Radian După cum știți
din clasele mai mici Măsura unui
unghi la centru este egală cu măsura
arcului mic cuprins între laturile
sale un unghi având măsura egală
cu 90 de grade se numește unghi
drept iar acesta subîntinde un
sfert de cerc iar un unghi având
măsura egală cu 180 de grade se
numește unghi alungit iar acesta
subîntinde un semicerc dacă efectuez
o rotație completă atunci obținem
un unghi cu măsura de 360 de grade
Așadar un cerc întreg are măsura
egală cu 360 de grade Până acum
am discutat despre măsura unghiurilor
în grade însă unghiurile se pot
măsura și în radiani Haide să vedem
ce este acela un Radian dacă unghiul
a o b subîntinde un arc având lungimea
egală cu raza cercului atunci măsura
unghiului AOB va fi egală cu un
Radian Așadar un Radian este măsura
unui arc de cerc având lungimea
egală cu raza cercului măsura în
radiani a unui arc de cerc respectiv
a unghiului la centru nu depinde
de raza cercului din care face
parte un radiani este unghiul pentru
care raportul dintre lungimea cercului
și rază este egal cu unu sa vedem
care este legătura dintre radiani
și grade nu știm că lungimea unui
cerc este egală cu 2 pi r dacă
un Radian corespunde unui arc de
lungime R atunci Câți radiani are
un cerc întreg Păi 2 pi radiani
pentru că un Radian este un unghi
care subîntinde un arc de lungime
l și atunci unghiul care subîntinde
un arc de lungime 2 pai are doi
pira Dihanie Deci un cerc întreg
are 2 pi radiani sau 360 de grade
de ce are loc egalitatea 360 de
grade egal cu 2 pi radiani Dacă
împărțim aceasta egalitate la 2
obținem că 180 de grade este egal
cu pi radiani Deci unghiului de
180 de grade îi corespund pirat
de ani Dacă împărțim acum la P
obținem că un Radian este egal
cu 180 de grade supra pi Deci Putem
afla câte grade are un Radian dacă
efectuăm această împărțire Haideți
să facem 180 împărțit la Pink Deci
180 împărțit la 3 1 5 obținem 50
și 7 Așadar un Radian are aproximativ
57 de grade nu trebuie să rețineți
acest lucru Însă este foarte important
să rețineți aceste două egalități
Așadar unui unghi cu măsura de
360 de grade îi corespund 2 pi
radiani iar unghiului cu măsura
de 180 de grade îi corespund Radian
de obicei pentru măsura în radiani
nu mai scriem cuvântul rad Dacă
nu apar grade atunci se subînțelege
că e vorba de măsura în radiani
de asemenea putem recunoaște o
măsură în radiani și prin faptul
apare pi Așa da să reținem că 180
de grade este egal cu pi radiani
Haideți acum să vedem Câți radiani
au 90 de grade dacă împărțim relația
de mai sus la 2 obținem că 90 de
grade este egal cu pi supra 2 radiani
Dacă împărțim prima relație la
trei obținem că 60 de grade este
egal cu pi supra 3 radiani Dacă
împărțim la 6 avem 30 de grade
egal cu pi supra 6 radiani sau
dacă împărțim egalitatea la patru
avem 45 de grade egal cu pi supra
4 radiani să vedem cum putem să
exprimăm în Radian măsura de 270
de grade observăm că 270 este egal
cu trei ori 90 de grade Deci avem
trei ori pe supra 2 egal cu 3 pi
supra 2 radiani Haide să vedem
cum putem să găsim o formulă prin
care se exprima în gradele în radiani
pentru aceasta vom folosi regula
de trei simpla dacă la 180 de grade
îi corespund pi Radian atunci la
o măsură de n grade o să îi corespunde
x radiani și avem x egal cu n grade
ori pi supra 180 Iată formula prin
care putem să transformăm grade
în radiani De exemplu dacă vreau
să transformăm 135 de grade în
radiani De ce an este 135 atunci
x va fi egal cu 135 pi supra 180
putem să simplificăm cu cinci 135
împărțit la 5 este 27 iar 180 împărțit
la 5 36 se mai simplifică cu 9
și ne rămâne 3 supra 4 Deci avem
3 supra 4 prin urmare 135 de grade
este egal cu 3 pi supra patru radiani
dacă dorim acum se transformă mă
radiani in grade folosim din nou
regula de trei simpla lapi radiani
le corespund 180 de grade și atunci
la n radiani o să le corespundă
o măsură de x grade x va fi egal
cu n ori 180 supra p Iată formula
prin care putem să transformăm
radiani in grade De exemplu dacă
vreau să transform în grade 5 pi
supra 4 radiani aplică în formula
aceasta și obținem că x este egal
Înlocuim pe and cu 5 p supra 4
și Putem să scriem astfel 5pi supra
4 ori 180 supra pii se simplifică
prin simplificăm 180 cu 4 ne rămâne
45 5 ori 45 este egal cu 225 de
grade prin urmare 5 pi supra 4
este egal cu 225 de grade
Măsurarea unghiurilor în grade și radianiAscunde teorie X
Navigare în lectii
Cumpara abonament
