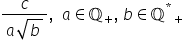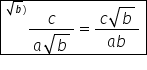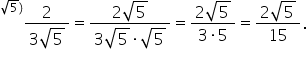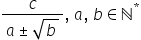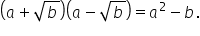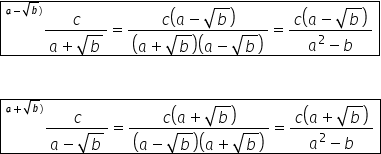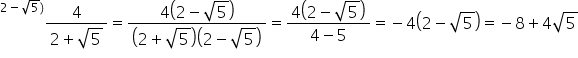Raționalizarea numitorului

să raționalizăm acum numitori de

forma avem aici două forme de fapt

a plus radical din b și a minus

radical din b mai întâi să ne amintim

Ce este aceea raționalizarea unui

numitor dacă avem un raport cum

e acesta 7 supra radical din 2

la numărător putem să avem Orice

număr real dar la numitor e important

faptul că avem un număr irațional

Haide să notăm radical din 2 aparține

lui R minus Q este prin urmare

un număr irațional în exerciții

este mai greu să lucrăm cu asemenea

în numere de aceea raționalizăm

numitorul acestui raport de fapt

ce face amplificăm acest raport

cu radical din 2 cu alte cuvinte

chiar cu radicalul care apare la

numitor și vom avea egal mai departe

linie de fracție 7 înmulțit cu

radical din 2 iar la numitor avem

radical din 2 înmulțit cu radical

din 2 egal cu vom avea șapte ori

radical din 2 adică 7 radical din

2 supra aici Cum obține radical

din 2 la pătrat Deci 2 iată că

vin tu un numitor irațional am

ajuns la un numitor rațional 2

este un număr rațional Hei acest

procedeu se numește raționalizarea

numitorului Cum raționalizăm acum

numitorul acestui raport Iată 8

supra 3 minus radical din 2 Ce

fel de număr este numitorul acestui

raport pe 3 minus radical din 2

este de fapt un număr irațional

aparțin mulțimii R minus Q acum

aceasta este forma de scriere a

acestui număr adică nu mai putem

să restrânge m sub o altă formă

această diferență Și așa se scrie

numărul nostru 3 minus radical

din 2 cum să facem acum ca să raționalizăm

acest numitor cu alte cuvinte nu

mai vrem să ne apară aici radical

din 2 Păi putem să facem în așa

fel încât în loc de radical din

2 să avem radical din 2 la pătrat

pentru că având aici exponentul

2 radicalul o să dispară e bine

putem să facem acest lucru astfel

vom amplifica acest raport cu suma

celor două numere aici avem diferența

lor și vom amplifica cu suma 3

plus radical din 2 și ai de să

notăm ce vom obține egal mai departe

cu la numărător avem 8p lângă 3

plus radical din 2 iar la numitor

avem diferența numerelor înmulțită

cu Deci înmulțită cu suma lor cu

3 plus radical din 2 Păi ne sună

cumva cunoscut un asemenea produs

dintre diferența a două numere

și suma lor Haideți să ne amintim

formula Deci dacă avem a și b două

numere reale când înmulțim diferența

numerelor cu suma lor vom obține

diferența pătratelor celor două

numere adică a pătrat minus b pătrat

și alte că astfel făcând acest

produs obținem pătratele celor

două numere Păi asta înseamnă că

vom avea aici și radical din 2

la pătrat Deci nu o să ne mai apară

radicalul Haide să notăm egal mai

departe Cum trecem linia de fracție

8 pe lângă 3 plus radical din 2

iar la numitor vom avea 3 la a

doua minus radical din 2 la a doua

Deci egal mai departe 8 pe lângă

3 plus radical din 2 supra avem

aici 9.900 Gal cu numitorul pe

care îl obținem este 7 La numărător

fie Putem să lăsăm scriere așa

Sau dacă vreți putem să desfacem

și parantezele Și atunci vom obține

24 plus 8 radical din 2 iată că

am obținut dintru un numitor număr

irațional un număr rațional a acest

procedeu se numește raționalizarea

numitorului cu alte cuvinte când

avem un numitor de această formă

Deci să luăm raportul 1 supra și

numitorul are această formă minus

radical din b unde a și b sunt

numere raționale și radical din

b este un număr irațional ca să

raționalizăm un asemenea la raport

la numărător putem să avem Orice

număr real am pus aici unul ca

să ne fie mai ușor la calcul Deci

casă raționalizăm vom amplifica

acest raport cu suma celor două

numere cu a plus radical din b

și vom avea la numărător avem a

plus radical din b iar la numitor

a minus radical din b înmulțit

cu a plus radical din b egal cu

numărătorul îl copiem iar la numitor

vom avea conform formulei pe care

am folosit o anterior avem diferența

dintre pătratele celor două numere

adică avem Aa pătrat radical din

b la pătrat însă radical din b

la pătrat știind că ne dă b de

ceai de să ștergem Și scrie direct

ca aici vom obține a minus b Deci

ce am obținut aici ce îți numitor

este un număr rațional dacă avem

însă raportul 1 supra a plus radical

din b deci aici nu mai avem diferența

celor două numere și suma lor voi

ideea de raționalizare este aceeași

diferența este singura diferență

este că acum cum amplifica a cu

A minus radical din b Deci amplificăm

cu diferența celor două numere

și egal mai departe cu la numărător

vom avea A minus radical din b

în timp ce la numitor vom avea

același produs care apare și aici

cu alte cuvinte rezultatul a pătrat

minus b tot așa număr rațional

Haideți acum să aplicăm aceste

două metode de raționalizare în

exerciții și avem acest raport

4 supra 2 plus radical din 5 avem

aici un număr rațional Acesta este

un număr irațional și avem sumă

între cele două numere atunci cu

cât vom amplifica complicat cu

diferența lor adică cu 2 minus

radical din 5 și vom obține linie

de fracție la numărător avem 4

pe lângă 2 minus radical din 5

iar la numitor avem 2 adunat cu

radical din 5 înmulțit cu 2 minus

radical din 5 numărătorul putem

să îl copie Deci avem 4 pe lângă

2 minus radical din 5 iar la numitor

vom avea diferența din 2 la a doua

și radical din 5 la a doua de diferența

dintre pătratele celor două numere

întotdeauna atenție obținem diferență

asta ne spune formula avem linie

de fracție 4 pe lângă 2 minus radical

din 5 iar Aici avem patru minus

cinci Păi patru minus cinci ne

dă minus unu practic Rezultatul

este minus acest număr împărțit

la minus sumă ne dă minus 4 pe

lângă 2 minus radical din 5 și

putem să desfacem și paranteza

Vom avea în minus 8 adunat cu 4

radical din 5 următorul exercițiu

12 radical din 3 supra radical

din 7 minus 1 avem aici un număr

irațional și aici un număr rațional

Nu contează că ordinea e diferită

față de cea de mai sus Avem tot

așa un număr irațional atunci cu

cât vom amplifica îi vom amplifica

ca și mai sus Haideți să facem

tot cu verde vom amplificat cu

suma acestor două numere cu radical

din 7 adunat cu 1 și vom obține

trece mai întâi linia de fracție

12 radical din 3 înmulțit cu radical

din 7 plus 1 iar la numitor vom

avea radical din 7 minus 1 înmulțit

cu radical din 7 plus 1 egal cu

copiem numărătorul aici radicali

din 7 plus 1 iar la numitor aplicăm

formula de șoma Bia așa radical

din 7 la pătrat minus 1 la pătrat

Deci este egal cu Avem 12 ori radical

din 3 ori radical din 7 plus unu

și aici vom avea șapte minus unu

adică ne dă 6 Păi chiar putem să

facem și câteva și o simplificare

de fac pentru că aici avem înmulțire

peste tot la numărător avem înmulțire

deci putem să simplificăm pe 12

și 6 prin șase ne rămâne aici 1

iar Aici doi și putem să desfacem

și paranteza vom avea 2 ori radical

din 3 ori radical din 7 înmulțim

aici radicalii Deci vom avea doi

radical din 21 adunat cu avem 2

radical din 3 înmulțit cu 1 adică

doi Deci plus 2 radical din 3 următorul

exercițiu 11 supra radical din

3 minus radical din 2 pe aici observăm

că avem diferența dintre două numere

Nu avem cum mai sus un număr rațional

și celălalt irațional ce ambele

numere sunt iraționale numitorul

este sigur număr irațional însă

cum face să raționalizăm un asemenea

rapport ideea de rezolvare este

aceeași adică vom amplifica acest

raport cu suma celor două numere

cu radical din 3 adunat cu radical

din 2 Dacă vom amplifica cu această

sumă atunci conform formulei vom

avea diferența dintre pătratele

celor două numere Deci nu o să

mai avem nici radical din 3 nici

radical din 2 și ambele vor fi

la pătrat Haide să notăm linie

de fracție la numărător 11 pe lângă

radical din 3 adunat cu radical

din 2 iar la numitor avem radical

din 3 minus radical din 2 pe care

îl înmulțim cu Raid cal din 3 plus

radical din 2 egal cu 3 cm Linia

de fracție 11 pe lângă radical

din 3 plus radical din 2 și la

numitor si vom obține Păi radical

din 3 la a doua din care scădem

pe radical din 2 la a doua Deci

vom avea numărătorul supra Haide

să notăm linie de fracție numărătorul

11 radical din 3 plus radical din

2 supra vom avea aici 3 minus 2

cu alte cuvinte Rezultatul este

11 pe lângă această paranteză dacă

vrem să desfacem paranteză Avem

11 radical din 3 adunat cu 11 radicali

din 2 și sa încheiat iată că și

în aceste situații putem să amplificăm

cu suma lor sau respectiv cu diferența

dacă aici avem suma și astfel raționaliza

numitorul