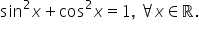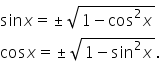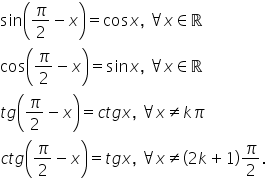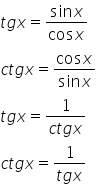Relații între funcții trigonometrice ale unui unghi (aplicații)

în acest clip o să facem două exerciții

în care vom calcula valorile unor

funcții trigonometrice primul exercițiu

se dă cosinus de x egal cu minus

3 supra 5 unde x este din intervalul

pi supra 2 pi avem Așadar un unghi

din cadranul al doilea și Săcele

să determinăm valorile tuturor

funcțiilor trigonometrice pentru

unghiul x pentru început este bine

să știm semnul acestor funcții

Iată un tabel cu semnul funcțiilor

trigonometrice pentru unghiurile

din cadranul 2 sinusul este pozitiv

cosinusul este negativ iar tangenta

și cotangenta sunt negative iar

mai jos avem un tabel cu formulele

pe care le vom aplica în aceste

exerciții câteva dintre aceste

formule au fost de dus în clipul

anterior pentru a determina sinusul

acestui unghi bun pornind de la

Formula fundamentală a trigonometriei

sin pătrat de x plus coș pătrat

de x este egal cu unu de aici deducem

că sinus de x este radical din

1 minus coș pătrat de x sinusul

în cadranul 2 este pozitiv Deci

în fața radicalului avem Semnul

plus sinus de x Zafira din 1 minus

cosinus este minus 3 supra 5 Deci

cost pătrat de x va fi 9 supra

25 obținem radical din 25 minus

9 16 supra 25 și egal cu 4 pe 5

pentru a calcula tangenta unghiului

x putem să aplicăm una dintre aceste

două formule sau mai simplu știind

că tangentă de x este și nu spre

cosinus sinus de x este 4 pe 5

iar cosinus de x este minus 3 pe

5 se simplifică 5 și ne rămâne

minus 4 pe 3 Iată tangenta este

negativă pentru unghiurile din

cadranul al doilea cotangentă de

x este 1 supra tangentă de x și

obținem minus trei supra patru

am aflat Așadar valorile tuturor

funcțiilor trigonometrice ale unghiului

x și trecem la exercițiul al doilea

se dă tangentă de x egal cu minus

1 pe 3 unde x este din intervalul

3 pi supra 2 2 pi avem Așadar 1

m din cadranul 4 și se cere să

aflăm sinus de x cosinus de x și

cotangentă de x pentru a exprima

sinusul în funcție de tangentă

vom aplica această formulăm Deci

avem sinus de x egal linie de fracție

tangentă de x supra plus minus

radical din 1 plus tangentă pătrată

de x egal tangenta este minus 1

pe 3 deocamdată nu scrie în semnul

radicalului și avem radical din

1 plus tangentă pătrată de x este

1 pe 9 sinusul în cadranul 4 este

negativ la numărător avem deja

un număr negativ prin urmare semnul

acestui radical va fi plus a astfel

încât semnul fracției să fie minus

egal cu minus 1 pe 3 supra radical

din 10 pe 9 egal cu minus 1 pe

3 supra radical din 10 pe 3 egal

cu minus 1 supra radical din 10

raționalizăm și obținem minus radical

din 10 supra 10 m Calculați sinusul

acestui unghi pentru a calcula

cosinus de x aplicăm această formulă

cosinus de x este radical din 1

minus sim pătrat de x sinus pătrat

de x este 1 pe 10 semnul în fața

radicalului va fi plus deoarece

funcția cosinus este pozitivă în

cadranul 4 și avem radical din

9 pe 10 egal 3 supra radical din

10 și egal cu 3 radical cal din

10 supra 10 și mai trebuie să aflăm

cotangentă de x cotangenta este

1 supra tangentă de x tangenta

este minus 1 pe 3 Deci cotangenta

va fi minus 3