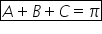Rezolvarea triunghiurilor

în această secvență vom rezolva

triunghiul oarecare a rezolva un

triunghi înseamnă ai găsit toate

laturile și unghiurile atunci când

se cunosc trei dintre acestea pentru

a rezolva triunghiurile oarecare

vom folosi teorema cosinusului

teorema sinusurilor și unele formule

trigonometrice învățate primul

exercițiu Se dă triunghiul abc

măsura unghiului a este egală cu

5 supra 12 radiani b este pi supra

3 ab are lungimea egală cu 5 unități

secere se rezolvă În triunghiul

abc mai exact Trebuie să găsim

măsura unghiului c și lungimea

laturilor AC și BC În orice triunghi

suma măsurilor unghiurilor este

egală cu 180 de grade sau pe radiani

deci a plus b plus c este egal

cu pi si va fi egal cu pi minus

a plus b egal cu pi minus a este

5 supra 12 iar b este pi supra

3 egal cu minus 9 pi supra 12 egal

cu 3 pe supra 12 simplificăm cu

trei și obținem că c este egal

cu pi supra 4 radiani pentru a

găsi lungimile laturilor AC respectiv

bc vom aplicate orie ma sinusurilor

și avem AB supra sinus de c este

egal cu bc supra sinus de a egal

cu AC supra sinus de b a b este

5 supra sinus de pi supra 4 este

egal cu bc supra sinus de a a este

5pi supra 12 și egal cu AC supra

sinus de b b este pi pe 3 nu știm

valorile pentru sinus de pi pe

4 și sinus de pi supra 3 Haideți

să calculăm și sinus de 5pi supra

12 sinus de 5pi supra 12 este egal

cu sinus 5 supra 12 se poate scrie

e supra 4 plus y supra 6 și acum

aplicăm în continuare formula pentru

sinus de a plus b ori amintesc

sinus de a plus b m este egal cu

sinus de a cosinus de b plus cosinus

de a sinus de b și atunci o să

avem sinus de pi supra 4 ori cosinus

de pi supra 6 plus cosinus de pi

supra 4 ori sinus de pi supra 6

egal sinus de pi pe 4 radical din

2 pe 2 ori cosinus de pi supra

6 este radical din 3 pe 2 plus

radical din 2 pe 2 ori 1 pe 2 egal

cu radical din 6 plus radical din

2 totul supra 4 și acum Revenim

la această relație și avem 5 supra

sinus de pi supra 4 este radical

din 2 pe 2 egal cu bc supra radical

din 6 plus radical din 2 supra

4 și egal cu AC supra sinus de

pi supra 3 este radical din 3 supra

2 de aici putem să calculăm mai

departe bc și ac bc este egal înmulțim

pe diagonală cu 5 ori radical din

6 plus radical din 2 supra 4 ori

2 supra radical din 2 egal aici

se simplifică cu 2 și obținem 5

radical din 2 aici de factor comun

pe radical din 2 pe lângă radical

din 3 plus 1 supra 2 radical din

2 egal în continuare cu 5 pe lângă

radical din 3 plus 1 supra 2 și

mai trebuie să îl aflăm pe ace

Ba ce va fi egal cu 5 ori radical

din 3 supra 2 ori 2 supra radical

din 2 egal cu 5 radical din 3 supra

radical din doi am aflat astfel

ac bc iar unghiul c este pi supra

4 radiani trecem în continuare

la al doilea exercițiu Se dă triunghiul

abc cu ab egal 4 radical din 2

BC este 4 pe lângă 1 plus radical

din 3 unghiul b are măsura egală

cu 45 de grade secere se rezolvă

În triunghiul abc mai exact trebuie

să calculăm AC a și c pentru a

calcula lungimea segmentului ac

o să aplicăm teorema cosinusului

și avem acela pătrat egal cu a

b la pătrat plus bc la pătrat minus

2-a b ori b c ori cosinus de 45

de grade AC la pătrat este egal

cu 4 radical din 2 la pătrat plus

bc la pătrat din este 4 la a doua

pe lângă 1 plus radical din 3 totul

la a doua minus 2 ori 4 radical

din 2 ori 4 pe lângă 1 plus radical

din 3 ori coș de 45 radical din

2 pe 2 face la pătrat este egal

cu 16 ori 232 plus 16 pe lângă

1 plus 2 radical din 3 plus 3 ani

și se simplifică 2 4 x 4 este 16

radical din 2 ori radical din 2

este 216 ori 232 pe lângă 1 plus

radical din 3 la pătrat egal cu

32 plus 16 Plus 32 radical din

3 plus 48 minus 32 minus 32 radical

din 3 se reduc niște termeni și

obținem acela pătrat egal cu 16

plus 48 adică 64 prin urmare AC

este egal cu opt mai trebuie să

calculăm măsura unghiului a și

măsura unghiului c pentru aceasta

vom aplicate rema sinusurilor și

avem a b supra sinus de c egal

cu AC supra sinus de b și egal

cu bc supra sinus de A și acum

înlocuim în această relație elementele

cunoscute AB este 4 radical din

2 supra sinus de c egal cu AC AC

este 8 supra sinus de b b este

45 de grade sinus de 45 este radical

din 2 pe 2 egal cu bc 4 pe lângă

1 plus radical din 3 supra sinus

de ei în continuare calculând sinus

de C din această relație sinus

de ce va fi egal cu 4 radical din

2 ori radical din 2 pe 2 ori 1

pe 8 egal cu 1 supra 2 în consecință

măsura unghiului c va fi egală

cu 30 de grade Și mai trebuie să

aflăm unghiul a putem să aflăm

fie din această relație sau mai

simplu a este 180 de grade minus

45 plus 30 a este egal cu 105 grade