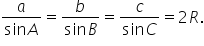Teorema sinusurilor (aplicații)

în acest clip o să facem două aplicații

la trimis sinusurilor prima problemă

Se dă triunghiul ABC se știe că

bc are lungimea egală cu 5 radical

din 2 raza cercului circumscris

triunghiului are lungimea egală

cu 5 unități se cere să calculăm

măsura unghiului a o să aplicăm

formula din teorema sinusurilor

și avem BC supra sinus de a egal

cu 2 r b c este 5 radical din 2

supra sinus de a egal cu 2 ori

5 10 din această relație obținem

că sinus de a este 5 radical din

2 supra 10 simplificăm cu 5 și

avem sinus de a egal radical din

2 supra 2 prin urmare măsura unghiului

a este egală cu 45 de grade a doua

problemă Se dă triunghiul abc cu

AC egal cu 8 cosinus de B este

2 radical din 2 supra 3 se cere

să calculăm raza cercului circumscris

triunghiului pentru a putea aplica

teorema sinusurilor va trebui mai

întâi să calculăm sinus de B pentru

aceasta vom aplica formula fundamentală

a trigonometriei sin pătrat de

b plus coș pătrat de B este egal

cu unu de aici obținem țin pătrat

de b egal cu 1 minus coș pătrat

de B sinus pătrat de B este egal

cu 1 minus cosinus de B este 2

radical din 2 supra 3 totul la

pătrat egal cu 1 minus 8 pe 9 și

egal cu 1 supra 9 Deci sinus de

B va fi egal cu 1 pe 3 și acum

putem să aplicăm relația din teorema

sinusurilor și avem ace supra sinus

de b egal cu 2 r AC este 8 supra

1 pe 3 egal cu 2 r 8 ori 3 este

egal cu 2 r împărțim egalitatea

la 2 și obțin M R egal cu 12