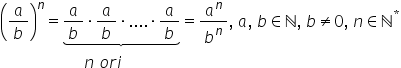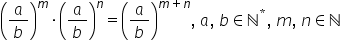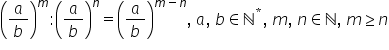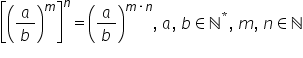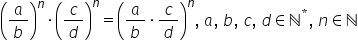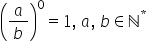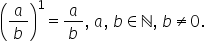Ridicarea la putere a fractiilor ordinare
Tag-uri
Partajeaza in Google Classroom
Transcript
ridicarea la putere a fracțiilor
să vedem ce înseamnă 3 supra 4
la puterea a doua ridica o fracție
la o putere înseamnă a o înmulțit
cu ea însăși de mai multe ori în
cazul nostru exponentul este doi
Deci o să înmulțim fracția 3 supra
4 cu ea însăși de două ori îmi
scrie egal cu 3 supra 4 ori 3 supra
4 atunci când trebuie să înmulțim
două fracții înmulțim numărătorii
între ei și numitorii între ei
o să obținem egal cu 3 ori 3 supra
patru ori patru dar trei ori trei
înseamnă trei la a doua chiar 4
x 4 este 4 la a doua observăm Așadar
că atunci când ridicăm o fracție
la o putere o să ridicăm și numărătorul
și numitorul la acea putere egal
mai departe 9 supra 16 un alt exemplu
1 supra 5 la puterea a treia va
fi egal cu 1 supra 5 ori 1 supra
5 ori 1 supra 5 egal mai departe
cu 1 ori 1 ori 1 supra 5 ori 5
ori 5 Care este egal cu 1 la a
treia supra 5 la a treia Observați
din nou că ridicăm și numărătorul
și numitorul la puterea a treia
1 la a treia este egal cu 1 5 la
a treia este 125 atunci Pentru
a ridica o fracție la o putere
ridicăm și numărătorul și numitorul
la acea putere adică a supra b
la puterea M va fi egal cu a la
n supra b la n continuare o să
deducem niște reguli de calcul
cu puteri prima regulă 3 supra
5 la puterea a doua ori 3 supra
5 la puterea a treia Încercăm să
găsim o regulă generală referitoare
la înmulțirea a doua puteri cu
aceeași bază 3 supra 5 la puterea
a doua este 3 la a doua supra 5
la a doua ori 3 la a treia supra
5 la a treia înmulțim iarăși numărătorii
între ei și numitorii între a egal
cu 3 la a doua ori 3 la a treia
supra 5 la a doua ori 5 la a treia
aici folosim regulile de calcul
cu puteri ale numerelor naturale
și 3 la a doua ori 3 la a treia
este egal cu 3 la a cincea deoarece
se adună exponenții supra 5 la
a cincea care se poate scrie mai
departe 3 supra 5 totul la puterea
a cincea e taxi pe la exponent
Observați ca exponentul rezultatului
este suma celor doi exponenți aceasta
va fi prima regulă de calcul cu
puteri și anume asupra pe la m
ori a supra b la n va fi egal cu
a supra b la puterea m plus n în
continuare vom de duce o altă regulă
de calcul cu puteri 2 supra 3 la
a șasea împărțit la 2 supra 3 a
doua egal mai departe cu 2 la a
șasea supra 3 la șasea împărțit
la 2 la a doua supra 3 la a doua
atunci când trebuie să împărțim
două fracții o să înmulțim prima
fracție cu invers a celei de a
doua deja fi egal cu 2 la a șasea
supra 3 la șasea ori 3 la a doua
supra 2 la a doua egal mai departe
cu 2 la a 6-a ori 3 la a doua supra
3 la a 6-a ori 2 la a doua 2 la
6 a se poate scrie 2 la a doua
ori 2 la a patra iar 3 la a doua
copiem supra trei la șasea se poate
scrie 3 la a doua ori 3 la a patra
iar pe 2 la a doua copiem observăm
că factorul 2 la a doua apare atât
la numărător cât și la numitor
înseamnă că putem să simplificăm
această fracție cu 2 la a doua
2 la a doua împărțit la 2 la a
doua a fi 1 observăm că și trei
la a doua se repetă înseamnă că
vom simplifica și cu 3 la a doua
obținem cu 1 și 1 la numărător
rămâne 2 la a patra iar la numitor
3 la a patra care se va scrie 2
supra 3 totul la puterea a patra
ne dăm din nou la exponentul rezultatului
și observăm că acesta este diferența
dintre cei doi exponenți inițial
a doua regulă de calcul cu puteri
va fi aceasta asupra Bella m împărțit
la a supra b la n va fi egal cu
a supra b la puterea n minus m
în continuare o să deducem a treia
regulă de calcul cu puteri 4 supra
7 la puterea a doua și totul ridicat
la puterea a treia să vedem ce
se va întâmpla cu exponenți în
acest caz 4 supra 7 la a doua este
4 la a doua supra 7 la a doua și
totul ridicat la puterea a treia
final mai departe cu 4 la a doua
supra 7 la a doua înmulțită cu
ea însăși de trei ori ori 4 la
a doua supra 7 la a doua ori 4
la a doua supra 7 la a doua enorm
de parte cu 4 la puterea a șasea
deoarece se adună exponenții iar
7 la 27 la a doua și 7 la a doua
va fi egal cu 7 la puterea a șasea
care sa va scriem 4 supra 7 totul
la puterea a șasea observăm că
exponentul rezultatului este produsul
dintre cei doi exponenți și atunci
Regula numărul 3 va fi aceasta
asupra B la m totul la puterea
n va fi egal cu a supra b la puterea
M Ori n și a patra regulă 2 supra
5 la puterea a doua ori 3 supra
4 la puterea a doua să vedem dacă
putem scrie Acest produs de două
puteri ca și puterea unui produs
2 supra 5 totul la a doua este
2 la a doua supra 5 la a doua ori
3 la a doua supra 4 la a doua egal
mai departe cu 2 la a doua ori
3 la a doua totul supra 5 la a
doua ori 4 la a doua dar 2 la a
doua ori 3 la a doua se poate scrie
2 ori 3 totul la a doua supra 5
x 4 totul la a doua egal cu 2 ori
3 supra 5 x 4 totul la puterea
a doua observăm Așadar că produsul
a doua puteri este egal cu puterea
produsului aici bineînțeles putea
face calculele în continuare și
obținem 6 supra 20 totul la puterea
a doua Care este egal cu 36 supra
400 putem să mai simplificăm cu
4 și obținem egal cu 9 supra 100
Regula numărul 4 va fi aceasta
a supra b la n ori c supra D la
n va fi egal cu a supra b o c supra
D totul la puterea n în continuare
o să facem câteva exerciții în
care vom aplica regulile învățate
până acum primul exercițiu cinci
supra opt la puterea a patra împărțit
la 5 supra 8 la puterea a doua
va fi egal conform celui de a doua
reguli cu 5 supra 8 la puterea
4 minus 2 adică 5 supra 8 la puterea
a doua Care este egal cu 5 la a
doua supra 8 la a doua egal cu
25 supra 64 al doilea exercițiu
să calculăm cu 1 supra 2 la puterea
a doua ori 1 supra 2 la puterea
a treia folosim prima regulă și
scrie egal cu 1 supra 2 la puterea
doi plus trei Adică 1 supra 2 la
a cincea egal cu unu la cincea
supra 2 la a cincea egal cu 1 supra
32 al treilea exemplu 7 supra 9
la puterea a doua și totul ridicat
la puterea a treia împărțit la
7 supra 9 la puterea a cincea conform
celei de a treia reguli prima fracție
se va scrie 7 supra 9 la puterea
doi ori trei adică la puterea a
șasea împărțit la 7 supra 9 la
puterea a cincea Care este egal
mai departe cu 7 supra 9 la puterea
6 minus cinci adică la puterea
întâia egal mai departe cu 7 supra
9 Orice fracție la puterea întâia
este ea însăși și ultimul exercițiu
2 supra 7 la puterea a doua ori
5 supra 2 la puterea a doua acest
produs de două puteri se poate
scrie egal cu 2 supra 7 ori 5 supra
2 totul la puterea a doua putem
să simplificăm pe diagonală deoarece
apare factorul 2 și la numărător
și la numitor o să simplificăm
Așadar cu 2 2 împărțit la 2 este
1 obținem 1 ori 5 Care este 5 supra
7 ori unu șapte totul la puterea
a doua egal mai departe cu 5 la
a doua supra 7 la a doua Care este
egal cu 25 supra 49
Ridicarea la putere cu exponent natural a fracțiilor ordinare pozitiveAscunde teorie X
Navigare în lectii
Cumpara abonament
