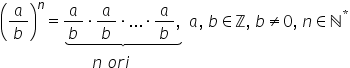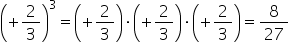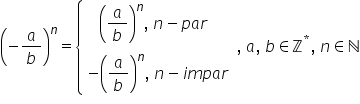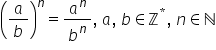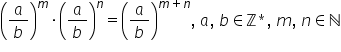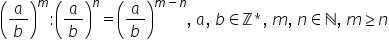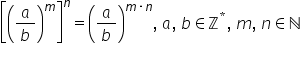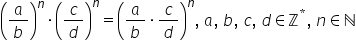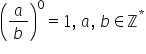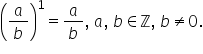Ridicarea la putere a numerelor raționale
Tag-uri
Partajeaza in Google Classroom
Transcript
a ridicat la o putere un număr
rațional înseamnă ale înmulțit
cu el însuși de mai multe ori de
exemplu dacă avem fracția a supra
b unde b este diferit de zero ridicată
la puterea n va fi egal cu a supra
b ori a supra b ori puncte puncte
ori a supra b de n ori n se numește
exponent iar a supra b se numește
bază de exemplu dacă avem fracția
plus 1 supra 2 la puterea a doua
aceasta va fi egală cu plus 1 supra
2 înmulțit cu plus 1 supra 2 plus
ori plus este plus și 1 ori 1 este
1 supra 2 adică patru să luăm și
eu număr negativ minus 1 supra
3 la puterea a 3-a definiție a
este egal cu minus 1 supra 3 ori
minus 1 supra 3 ori minus 1 supra
3 minus cu minus este plus iar
plus ori minus este minus 1 supra
3 ori 3 ori 3 este 3 la a treia
adică 27 pentru ridicarea la putere
a numerelor raționale avem aceleași
reguli de calcul ca și la numerele
raționale pozitive învățate în
clasa a șasea dar ținem cont și
de regula semnelor să vedem în
continuare Care sunt aceste reguli
de calcul cu puteri fracția a supra
b la puterea n este egală cu a
la n supra b la n dacă avem un
număr rațional negativ minus a
supra b la o putere n rezultatul
va fi pozitiv și va fi egal cu
a supra b la n Dacă n este par
și minus a supra b la n Dacă n
este impar alte cuvinte Dacă un
număr rațional negativ se ridică
la o putere pară Rezultatul este
pozitiv iar Vica la o putere impară
Rezultatul este negativ atunci
când înmulțim două puteri cu aceeași
bază exponenții se adună la împărțire
exponenții se scad atunci când
ridicăm o fracție la puterea 0
Rezultatul este 1 iar o fracție
de formă a supra b la puterea M
și totul dedicat la puterea n va
fi egal cu a supra b la puterea
n ori n Deci înmulțim exponenții
iar produsul de formă a supra b
la n ori c supra de la n este egal
cu a supra b ori c sută D totul
la puterea n să facem acum câteva
exerciții în care vom aplica aceste
reguli de calcul cu puteri primul
exercițiu minus 4 supra 7 la puterea
a șasea împărțit la minus 4 supra
7 la puterea a patra Cum aplica
această regulă deoarece avem o
împărțire de două puteri cu aceeași
bază Deci exponenții o să îi scădem
a fi egal cu minus 4 supra 7 la
puterea 6 minus 4 Care este egal
cu minus 4 supra 7 la puterea a
doua ținem cont de faptul că doi
este un exponent par iar atunci
când ridicăm un număr negativ la
o putere pară Rezultatul este pozitiv
Așadar rezultatul va avea Semnul
plus iar 4 la a doua este 16 și
7 la a doua este 49 al doilea exercițiu
minus 2 supra 3 la puterea a doua
și totul ridicat la puterea a doua
va fi egal cu minus 2 supra 3 aici
înmulțim exponenții doar 2 este
4 patru este iarăși un exponent
par Deci rezultatul va fi pozitiv
2 la a patra este 16 iar 3 la a
patra este 81 al treilea exercițiu
minus 1 supra 2 la puterea a doua
ori minus 1 supra 2 la puterea
a treia atunci când înmulțim două
puteri cu aceeași bază exponenții
se adună Deci scrie minus 1 supra
2 la puterea a cincea numărul 5
fiind un exponent impar Rezultatul
este negativ deci punem semnul
minus 1 la puterea a 5-a este 1
2 la puterea a 5-a este 32 și ultimul
exercițiu minus 5 supra 9 la puterea
a zecea împărțit la minus 5 supra
9 la puterea a doua și totul ridicat
la puterea a cincea o să copiez
prima fracție minus 5 supra 9 la
puterea a zecea împărțit la minus
5 supra 9 aici înmulțim exponenții
de 5 este 10 acum trebuie să împărțim
două puteri cu aceeași bază exponenții
se scad scrie minus 5 supra 9 la
puterea 10 minus 10 adică 0 care
va fi egal cu unu de orice orice
număr rațional ridicat la puterea
0 este 1
Ridicarea la putere a numerelor raționaleAscunde teorie X
Navigare în lectii
Cumpara abonament
