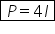Rombul- aplicații

în continuare o să facem două probleme

în care o să aplicăm proprietățile

rombului O primă problemă rombul

m n p q are perimetrul de 72 cm

și măsura unghiului n p m egală

cu 30 de grade Calculați lungimea

diagonalei nq pornim de la formula

de calcul a perimetrului unui romb

perimetrul lui mnpq este egal cu

4 ori lungimea unei laturi notăm

latura rombului cu el și se știe

că acest perimetru este egal cu

72 cm de aici putem să calculăm

lungimea laturii aceasta este egală

cu 72 împărțit la patru latura

rombului va fi egală cu 18 cm mai

trebuie să calculăm lungimea diagonalei

nq știind că între un romb diagonalele

sunt și bisectoarele unghiurilor

cu alte cuvinte m p este bisectoarea

unghiului n p q înseamnă că aceste

două unghiuri sunt congruente prin

urmare măsura unghiului MPQ va

fi egală cu 30 de grade triunghiul

MPQ este un triunghi isoscel dar

în acest triunghi isoscel avem

un unghi cu măsura de 60 de grade

este vorba de unghiul p iar un

triunghi isoscel care are un unghi

cu măsura de 60 de grade este un

triunghi echilateral astfel triunghiul

n p q va fi un triunghi echilateral

iar lungimea diagonalei mq a fi

egală cu lungimea laturii rombului

NP să scriem cele discutate până

acum dacă m n p q este romb înseamnă

că diagonala mp este și bisectoarea

unghiului npq dar se știe din ipoteză

că măsura unghiului NPM este egală

cu 30 de grade prin urmare măsura

unghiului npq a fi egală cu 30

de grade unghiurile acestea sunt

congruente înseamnă că măsura unghiului

n p q este egală cu 60 de grade

triunghiul mnpq este un triunghi

isoscel pentru că laturile rombului

sunt congruente Așadar n p e congruent

cu pq dar un triunghi isoscel care

are un unghi cu măsura de 60 de

grade este echilateral Deci triunghiul

MPQ este echilateral și astfel

va rezulta că n q are aceeași lungime

cu NP și cu pq și egale cu 18 cm

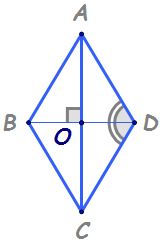
trecem la următoarea problemă În

figura de mai jos este reprezentat

rombul Star iar p și q sunt mijloacele

laturilor este și a Arătați că

triunghiul n p q este isoscel iar

la punctul b dacă este este egal

cu 2 cm Calculați perimetrul rombului

demonstrație începem cu punctul

a us arătăm că triunghiul n p q

este isoscel trebuie să arătăm

că acesta are două laturi congruente

vom arăta că r p este congruent

cu nq pentru aceasta căutăm să

încadrăm cele două laturi în două

triunghiuri a căror congruență

poate fi demonstrată o să unim

punctele d și R și astfel se formează

două triunghiuri Triunghiul p p

r și T q r o Să arătăm că aceste

două triunghiuri sunt congruente

dacă este aer este romb înseamnă

că este are aceeași lungime cu

ta însă pești și q sunt mijloacele

laturilor lui prin urmare segmentul

p t va fi congruent cu segmentul

pq lungimile acestor segmente sunt

egale ele fiind jumătăți ale unor

segmente congruente dacă este aer

este romb înseamnă că este este

egal cu a Dacă p și q sunt mijloacele

laturilor înseamnă că și aceste

segmente pe t și T q sau ciute

au aceeași lungime mai știm că

diagonala ter este și bisectoare

a unghiului t astfel unghiul este

r acesta este congruent cu unghiul

q r se scrie acest lucru pe R este

bisectoarea unghiului și astăzi

rezultă că unghiul pe p r este

congruent cu unghiul q r mai știm

că aceste două triunghiuri au o

latură comună aceasta este latura

p r Haideți să scriem mai jos elementele

congruente am arătat Așadar că

peste este congruent cu segmentul

qt apoi am arătat că unghiul bad

este congruent cu unghiul q p r

segmentul stayer este congruent

cu segmentul ter fiind o latură

comună din cele trei relații va

rezulta conform cazului de congruență

latura unghi latura că triunghiul

p p r este congruent cu triunghiul

q r congruență acestor triunghiuri

implică congruența segmentelor

pe r și q r am arătat astfel că

triunghiul p q r este un triunghi

isoscel pentru că are două laturi

congruente pe R este congruentă

cu latura q a r am terminat cu

punctul A continuăm cu punctul

b dacă este este egal cu 2 cm Calculați

perimetrul rombului având în vedere

că punctul p este situat la mijlocul

laturii este înseamnă că lungimea

acestei laturi este va fi de două

ori mai mare decât lungimea segmentului

Espace Știind că p este egal cu

pete și egal cu 2 cm din ipoteză

prin urmare este este egal cu 2

ori 2 și egal cu 4 cm Deci latura

rombului este 4 cm Perimetrul acestui

romb Star este patru ori lungimea

unei laturi egal cu 4 ori 4 ori

424 2 reținem 4 x 4 16 și cu 218

18 cm