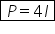Rombul

în această lecție o să vorbesc

despre romb și proprietățile acestuia

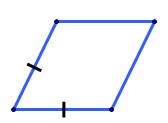
o să încep cu definiția Paralelogramul

cu două laturi alăturate congruențe

se numește romb având în vedere

că rombul este un paralelogram

particular acesta va avea toate

proprietățile paralelogramului

Laturile opuse vor fi paralele

două câte două Laturile opuse sunt

congruente două câte două unghiurile

opuse sunt congruente iar unghiurile

alăturate sunt suplementare dacă

Laturile opuse sunt congruente

Dar prin definiție rombul are și

laturile alăturate congruente va

rezulta că toate cele patru laturi

ale rombului sunt congruente Așadar

Aceasta este o consecință a definiției

și a Proprietăților paralelogramului

în cazul rombului a b c d a b va

fi egală cu b c egal cu c d și

egal cu d a în plus diagonalele

acestui romb se înjumătățesc dacă

construim diagonalele observăm

că punctul de intersecție al acestora

este situat la mijlocul fiecare

diagonale în plus față de aceste

proprietăți pe care le avea și

paralelogramul rombul are două

proprietăți specifice acestor și

enunțate sub forma unor teoreme

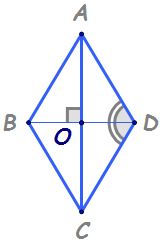
o să încep cu prima teoremă diagonalele

unui romb sunt perpendiculare Așadar

avem un romb ABCD și trebuie să

demonstrăm că ac este perpendiculară

pe b d având în vedere a că a b

c d este un romb înseamnă că laturile

sale sunt congruente va rezulta

că AB este egală cu ad Deci aceste

două laturi au aceeași lungime

rezultă din aceasta egalitate că

triunghiul ABD este un triunghi

isoscel o este mijlocul diagonalei

BD Deci b o este egal cu OD pentru

că o este mijlocul este mediană

în acest triunghi isoscel na rezultat

că a o este și înălțime înseamnă

că a o este perpendiculară pe BD

am arătat că diagonalele unui romb

sunt perpendiculare este valabilă

și reciproca aceste teoreme un

paralelogram cu diagonalele perpendiculare

este romb Deci pentru a demonstra

ca un paralelogram este romb și

arătăm că el are două laturi consecutive

congruente fie arătăm că diagonalele

sunt perpendiculare o altă proprietate

a rombului este enunțată sub formă

de aur ma numărul 3 diagonalele

unui romb sunt bisectoarele unghiurilor

am În rombul ABCD trebuie să arătăm

că diagonalele acestuia adică segmentele

AC și BD sunt și bisectoarele unghiurilor

m arăta că unghiul b o este congruent

cu unghiul d a o și în mod similar

se va arăta că unghiul b c o va

fi congruent cu unghiul d c o unghiul

ab o este congruent cu unghiul

c b o unghiul a d o este congruent

cu unghiul c d o pentru a demonstra

că aceste două unghiuri sunt congruente

le încadrăm în triunghiurile abe

o și a d o a căror congruență poate

fi demonstrată cele două triunghiuri

au următoarele elemente congruente

a b este congruentă cu Ade pentru

că rombul are toate cele patru

laturi congruente știind că diagonalele

rombului se înjumătățesc înseamnă

că Punctul o este mijlocul diagonalei

BD Deci segmentul v o este congruent

cu o d și cele două triunghiuri

au Latura comună AO va rezulta

conform cazului latura latura latura

ca aceste două triunghiuri sunt

congruente demonstrație știind

că a b c d este romb iar rombul

are toate laturile congruente A

rezultat că AB este congruent cu

ad o este mijlocul diagonalei BD

putem scrie că b o este congruent

cu OD iar a o este o latură comună

a celor două triunghiuri a o este

congruent cu AO unde o latură comună

din aceste trei relații rezultat

coaforul cazului de congruență

lectură lectură lectură că triunghiul

abe o este congruent cu triunghiul

def ia congruență acestor două

triunghiuri implică și congruența

unghiurilor b a o și de AO am demonstrat

prima relație rezultat dar că AO

respectiv AC este bisectoarea unghiului

b a d a c bisectoarea unghiului

b a d în mod Analog se demonstrează

și congruență a celorlalte unghiuri

se folosește metoda triunghiurilor

congruente și se arată că BD este

și a bisectoare este valabilă și

reciproca aceste teoreme teorema

numărul 4 Dacă intru în paralelogram

o diagonală este și bisectoare

atunci paralelogramul este romb

pentru a demonstra ca un paralelogram

este romb putem să aplicăm această

teoremă reciprocă și Să arătăm

că una din diagonale este și bisectoarea

unghiului în continuare să vedem

cum putem să calculăm perimetrul

unui romb știind că perimetrul

unui patrulater în general este

suma lungimilor laturilor Deci

perimetrul lui ABCD va fi egal

cu ab plus bc plus c d plus a d

Haideți sănătos este laturi cu

l mic egal în continuare cu el

cu el plus L plus l egal cu 4 L

Deci formula de calcul pentru perimetrul

unui romb este patru ori latura

rețineți această formulă pentru

că se va folosi în rezolvarea exercițiilor

și problemelor în continuare o

să facem o aplicație Aflați lungimea

diagonalei a c a rombului a b c

d Cunoscând măsura unghiului bcd

de 120 de grade și perimetrul rombului

este egal cu 80 centimetri pornind

de la datele problemei știind Perimetrul

rombului perimetrul lui ABCD este

egal cu 4 ori lungimea unei laturi

adică 4 el notăm laturile rombului

cu el și egal mai departe cu 80

cm kasel aflăm pe el o să mai scriu

o dată această ecuație cu necunoscuta

al împărțim această relație la

4 obținem l egal cu 80 împărțit

la 4 egal cu 20 Deci latura rombului

este 20 cm în cerate trebuie să

aflăm diagonala AC știind că diagonala

AC este și bisectoarea unghiului

bcd înseamnă că măsura unghiului

BCA va fi de 60 de grade triunghiul

ABC este un triunghi isoscel pentru

că are două laturi congruente și

mai mult El are și un unghi cu

măsura de 60 de grade deja fie

un triunghi echilateral înseamnă

că laturile sale vor fi congruente

Deci diagonala AC va avea lungimea

egală cu lungimea laturii rombului

adică cu 20 cm nu scrie că a b

c d fiind un romb rezultă că AB

este egală cu bc rezultă triunghiul

abc isoscel dar tot din faptul

că a b c d este un romb rezultă

că ac este bisectoarea unghiului

b c d rezultă că măsura unghiului

BCA este egală cu 60 de grade din

cele două relații rezultă că triunghiul

abc este echilateral Un triunghi

echilateral are toate laturile

egale va rezulta că ac este egală

cu AB și egal cu bc mai departe

și egal cu 20 cm