Tabelul de variație și monotonia funcției de gradul II
Tag-uri
Partajeaza in Google Classroom

Transcript
în această lecție vom face Funcția
de gradul al doilea și anume tabelul
de variație și monotonia acesteia
fie funcția f definită pe r cu
valori in R cu f de x egal cu x
pătrat plus bx plus c așa după
cum am discutat în lecția precedentă
o funcție de gradul al doilea are
un mod specific de reprezentare
a parabolei practica graficului
funcției în funcție de valoarea
coeficientului a real diferit de
0 astfel pentru a pozitiv graficul
era convex dacă aduceți aminte
spuneam ține apă respectiv pentru
a mai mic decât 0 Deci negativ
graficul este concav Da sau parabolă
este concavă Da și nu ținea apă
Deci ține apă nu ține apă pentru
a face o discuție teoretică și
practică asupra monotoniei și a
tabelului de variație corespunzătoare
funcțiilor de gradul al doilea
este necesar să Observați sau să
vizualizați că atunci când aul
este pozitiv graficul este convex
Funcția de gradul al doilea are
un punct de minim adică parabola
coboară până la un anumit punct
după care aceasta urca sau reprezentarea
grafică este făcută astfel încât
așa cum vă spuneam să coboare până
la un anumit punct respectiv să
urc în continuare la acel punct
către O să vedeți plus infinit
așa cum arăt punctul de pe parabolă
până la care se coboară și de la
practic se urcă în cazul în care
vorbim de a pozitiv când să comentăm
în mod cert că punctul la care
se coboară și respectiv de la care
se urcă este punct de minim punctul
de care comentam aici în mod Teoretic
în motor etic îl pun numim acest
punct de minim valoarea minimă
a funcției f pe tot același principiu
atunci când a este negativ graficul
este concav Funcția de gradul al
doilea are punct de maxim adică
parabola urcă până în tu un pumn
după care coboară exact ce va arăta
nu ține apă urcă până la acest
punct coboară de la acest punct
astfel că acesta este un punct
de maxim iar în mod Teoretic în
numi acest punct valoare maximă
a funcției f în mod clar în acest
moment întrebarea logică ce trebuie
pusă este Cum se determină matematic
sau Teoretic acest punct punctul
Maxim sau minim după caz răspunsul
la această întrebare implică două
noțiuni teoretice importante și
anume vârful parabolei notați cu
p mare și forma canonică a funcției
f ca orice punct al graficului
reprezentat în sistem cartezian
x o y punctul B vârful na are două
coordonate X V numit ascii să dacă
va aminti și y v numit ordonată
astfel vârful de coordonate x vârf
vârf este de fapt punctul de minim
dacă ai este pozitiv sau punctul
de maxim dacă a este negativ coordonatele
Vârfului x vârf respectiv vârf
Deci așa cum spuneam abscisa respectiv
ordonata sunt determinate în mod
Teoretic și practic din forma canonică
a funcției f astfel funcția f definită
pe r cu valori in R cu f de x egal
cu ax pătrat plus bx plus c a reforma
canoni e de x egal cu a pe lângă
x plus b supra 2-a la pătrat plus
minus Delta supra 4-a o verificare
acestui aspect Teoretic și mai
clară a formei canonice constă
în a calcula dacă vreți forma canonică
a dezvolta forma canonică și a
verificat dacă aceasta duce la
forma clasica descrierea funcției
de gradul al doilea și atunci avem
A pe lângă x plus b supra 2-a totul
la pătrat plus minus Delta supra
4-a egal cu a A1 Da am ridicat
la pătrat însemnat x pătrat aduceți
aminte că aveți formulă clară cu
a plus b la pătrat care înseamnă
realitate a pătrat plus 2ab plus
b pătrat formulă pe care o aplică
formula de calcul prescurtat și
atunci x pătrat plus doi ori x
ori b supra 2-a acesta fiind B1
students formula Na am închis sevidan
paranteza plus la un copil în aceste
condiții nu am făcut decât să desfac
paranteze adică a ori x pătrat
plus a ori doi ori x ori pe supra
2-a plus b pătrat supra 4-a pătrat
înmulțit cu a se va reduce a cu
apă trat și atunci rămâne de pătrat
supra 4-a în aceste condiții văd
clar că doi se simplifică cu 2
a se simplifică cu ei și mai mult
decât atât în continuare traduc
ceea ce înseamnă Deltă mai clar
pe pătrat minus patru ace astfel
obținem ax pătrat așa cum va spus
aista redusă rămas expeed pot să
scriu pe x Da și pentru că am același
numitor pentru aceste două fracții
le pot scrie Sub aceeași După același
numitor pentru aceeași atunci am
de pătrat minus b pătrat minus
în fața parantezei schimbă semnele
tuturor termenilor din paranteză
drept pentru care minus cu minus
de aici plus plus patru ace ceea
ce înseamnă că după ce am gratis
pe pătrat cu pe pătrat Vedeți și
zero obțin ax pătrat plus bx plus
spuneam am redus rămâne patru ace
supra 4-a în mod concret 4-a cu
4-a se reduce atunci obțin fără
doar și poate ax pătrat plus bx
plus c Observați aceasta este forma
canonică aceasta este forma Standard
la care este dată orice funcție
de gradul al doilea Deci e corect
să afirm că forma canonică a funcției
f este dată de această formă informat
ca nu Nica funcții de gradul al
doilea se pot determina ușor ați
cisa respectiv ordonața Vârfului
parabolei astfel din forma canonică
f de x egal cu a pe lângă x plus
b supra 2-a la pătrat minus plus
minus Delta supra 4-a prin egalarea
acestui termen cu 0 Poți să îmi
rezulte în realitate că x plus
b supra 2-a la pătrat este întrucât
aul stații este diferit de 0 vă
aduceți aminte că orice funcție
de gradul al doilea are are n diferit
de 0 pentru ca un pătrat să facă
0 fără doar și poate valoare ridicată
la pătrat este de aici se scoate
x egal cu minus b supra 2-a prin
trecerea în partea cealaltă termenului
de la doi Acu e Vitan semn contrar
în acest moment poți să afirm că
x vârf sau abscisa Vârfului este
minus b supra 2 ab determinată
aici pentru a determina ordonata
Vârfului va trebui să calculăm
pentru xvr determinat minus b supra
2-a fdx VR care fără doar și poate
va duce la obținerea ordonate așa
cum am spus adica lui y v minus
Delta supra 4-a de ce Pentru că
ei din formulă Cum x plus b supra
2-a totul la pătrat este 0 divided
va fi înlocuit Paul zero zero Dar
de ce aici obțin 0 praf pentru
care fără doar și poate e y e parfum
în A minus Delta supra 4-a sunt
în măsură garantat să afirm că
vârful este de coordonate minus
b supra 2-a respectiv minister
dar supra 4-a în continuare în
acest moment sunt în măsură să
afirm că atunci când a este pozitiv
funcția f definită pe r cu valori
in R cu f de x egal cu x pătrat
plus bx plus c amintesc a b c valori
reale cu a diferit de 0 admite
punct de minim pe mare de coordonate
x perfect vârf cu X vârf minus
pe supra 2-a și y v minus de Artă
a supra 4-a în plus pot să afirm
fără discuții că funcția este strict
descrescătoare adică așa cum va
arăta mai devreme coboară din intervalul
minus infinit minus b supra a și
este strict crescătoare iar vin
și spun Cum va arăta mai devreme
urcă Da cum voi evidenția în pe
grafic pe intervalul minus b supra
2-a plus infinit în aceeași ordine
de idei atunci când a este negativ
funcția f definită pe r cu valori
in R cu f de x egal cu x pătrat
plus bx plus c admite punct de
maxim b de coordonate x sfârșit
cu vârf cu X vârf minus b supra
2-a minus 3 supra 4-a și în mod
concret funcția este strict crescătoare
adică urcă pe intervalul minus
infinit minus b supra 2-a și este
strict descrescătoare sau coboară
așa cum afirmă pe intervalul minus
b supra 2-a plus infinit sub forma
unui tabel numit tabel de variație
se pot evidenția noțiunile teoretice
comentate mai sus astfel pentru
a pozitiv tabelul de variație pe
prima linie x pe a doua din f de
x x aparține lui r știind da așa
e de la minus infinit la plus infinit
x vârf evitant trebuie să apară
între valorile lui e Eti are valoare
vârf asociată lui x v r astfel
că de la minus infinit la xvr descrește
funcția de la ex vârful la plus
infinit crește funcția cum spuneam
x vârf vârf este un punct de minim
pe exactă același principiu dacă
ai este negativ în tabelul de variație
pe prima linie se trec palariile
cum spuneam ale lui x la momentul
ăsta minus infinit plus infinit
întrucât așa cum exprimăm x aparține
lui r x vârf de terminat iar pe
a doua linie a tabelului f de x
respectiv vârf asociat punctului
xvr de la minus infinit la X vârf
funcția crește de la X vârf la
plus infinit funcția scade așa
cum spuneam acesta este punctul
de Max și mai clar vârf Da și nu
ca și în celălalt punctul de minim
are valoare V valoare minimă punctul
de maxim are valoare are maximă
a funcției Evident așa cum spuneam
aici funcție este descrescătoare
aici funcția este crescătoare În
egală măsură aici funcția crește
iar Aici funcția cade

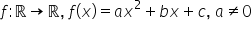
.JPG)

.JPG)

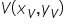 se numește vârful parabolei.
se numește vârful parabolei.