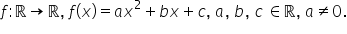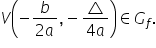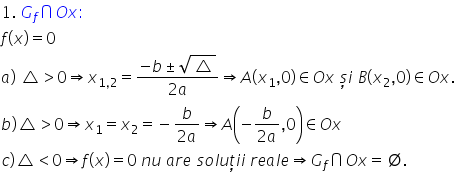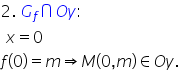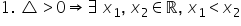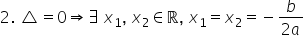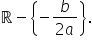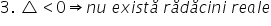Semnul funcției de gradul al doilea

în această lecție vom face Funcția

de gradul al doilea și mai clar

poziții relative ale graficului

funcției și semnul acesteia atunci

când discuțiile teoretice și practice

au drept țintă determinarea semnului

funcției de gradul al doilea este

important de înțeles că poziția

relativă a graficului funcției

față de axa o x în sistemul cartezian

x o y este hotărâtoare vom vedea

în continuare Cum acționează această

poziție asupra semnului funcții

gradul al doilea astfel atunci

când parte din graficul funcției

se află deasupra axei o x funcția

are valori pozitive vom afirma

că fdx este pozitiv sau că y este

pozitiv atunci când parte din graficul

funcției se află sub axa o y funcție

are valori negative astfel că palme

afirma că fdx este negativ Deci

ys3d negativ important în acest

moment este să înțelegeți că parte

din graficul funcției și un caz

și celălalt este de fapt o secțiune

din grafic această secțiune are

fără discuții puncte ce aparțin

graficului funcției puncte de forma

M mare de coordonate x y ampere

amintesc xm era acciza unui punct

chemi era ordonata unui punct în

sistem cartezian x o y cu x m aparține

lui r aer în acest moment joacă

rolul Domeniului funcției de gradul

al doilea și y altfel spus dacă

m de coordonate x y m aparține

graficului funcției cu e f definită

pe r cu valori în F și f de x egal

cu x pătrat plus b c cu a diferit

de 0 era foarte important de reținut

aspectul acesta și a b c aparțin

lui A deci coeficienți reali atunci

x x m x m d este egal cu y e Da

și sau e f d x m în reprezintă

de fapt a ori x m la a doua de

ce nu crezi când funcționa plus

bx plus c Dacă M este pozitiv reprezentarea

punctului m Da mai sus amintit

de pe grafic este deasupra axei

o x fiind pozitiv după cum știți

valorile pozitive ale lui y din

tapate deasupra ox x în aceeași

ordine de idei Dacă ai ce ritm

este negativ reprezentarea punctului

m de pe grafic este supa sa o maimuță

decât atât făcând conexiunea cu

o noțiune teoretică cunoscută și

mai clar intersecția graficului

cu axele de coordonate atunci când

dorim să determinăm Intersecția

cu Axa o x este necesar să calculăm

f de x egal cu zero ceea ce înseamnă

fără doar și poate că se va obține

ecuația de gradul al doilea ax

pătrat plus bx plus c egal cu 0

ecuații care în funcție de valoarea

lui Delta Care Urca și formulă

de calcul a avea b pătrat minus

4 AC are trei cazuri de discuție

cunoscute și mai clar Delta putea

să fie Delta putea să fie egal

cu 0 respectiv Delta putea să fie

pozitiv Evident din calcul astfel

că atunci când Delta era negativ

ecuația nu are rătăcire ale adică

X1 și X2 nu aparțin lui R când

Delta egal cu 0 ecuația are două

rădăcini reale egale sau confundate

dacă fac duceți aminte mai clar

X1 egal cu x 2 Diner respectiv

atunci când Delta era pozitiv ecuația

are două rădăcini reale distincte

mai clar x 1 x 2 aparține lui r

și foarte important X1 este diferit

de x 2 astfel că intersecție a

graficului funcției cu Axa o x

adică e f de x egal cu zero așa

cum am afirmat aici presupune tot

trei situații teoretice situația

a în care graficul nu intersectează

axa o x situația b atunci când

graficul intersectează axa o x

Evident într un singur punct respectiv

situația Si atunci când graficul

intersectează axa o x în două puncte

distincte mai clar atunci când

nu intersectează axa suntem pe

Delta negativ deci pe situația

Delta negativ atunci când intersectează

Accent un singur punct m pe situația

când Delta este egal cu 0 Iar atunci

când intersectează axa în două

puncte distincte de pe situația

cu Delta mai mare ca 0 De ce concluzia

de mai sus exprimat Păi axa o x

este axa pe care sunt reprezentate

valorile x ale Domeniului domeniul

este el Deci axa o x este acel

aer domenii dacă Delta este negativ

X1 și X2 nu aparțin lui R Teoretic

Da Asta înseamnă că valorile x

ale Domeniului nu pot fi așezate

sau dispuse pe axa o x ceea ce

înseamnă fără discuții că nu există

valori sau puncte m de coordonate

x y ale graficului ce pot fi dispuse

pe axa o x motiv pentru care fără

discuții afirmăm că graficul nu

intersectează axa o x dacă Delta

este egal cu 0 atunci știm că X1

egal cu x 2 și sunt reale Deci

valoare X1 care coincide cu valoarea

X2 poate fi așezată sau dispusă

pe axa o x deci pe axa numerelor

reale graficul în această situație

va intersecta sau x într un singur

punct M de coordonate X10 sau câtea

foarte ochii să spun x20 deoarece

X1 egal 0 sau În egală măsură fdx

2 egal 0 Dar cum X1 coincide cu

X2 am preferat să scriu doar o

singură variantă dacă Delta este

pozitiv atunci X1 și X2 aparțin

lui R asta înseamnă că X1 este

diferit de X2 și atunci valorile

X1 și X2 pot fi așezate sau dispuse

pe axa o x graficul funcției va

intersecta axa o x în două puncte

Praktiker unul de coordonate x

1 și 0 respectiv m2 de coordonate

x 2 și 0 deoarece f de x 1 este

garantat 0 este soluția ecuației

respectiv țuica cu 0 pentru înțelegere

Cât mai exact acelor exprimate

mai sus voi reprezenta în continuare

în mod grafic pozițiile relative

ale graficului funcției față de

axa OY Aici este important să vă

amintiți că în funcție de valoarea

coeficientului real a diferite

0 reprezentarea graficului este

convex sau afirmăm noi ține apă

sau concav practic nu ține apă

sau altfel spus au lira pozitiv

respectiv ale era negativ astfel

că în continuare reprezentările

grafice sunt următoare pe situația

când a este pozitiv avem Delta

negativ și atunci vine apă Da e

convexă Da dar nu intersectează

axa o x atunci când Delta este

egal cu 0 in ea pa Da intersectează

axa o x în singur punct atunci

când Delta este pozitiv ține apă

intersectează în două puncte Da

repeți situația când ai este pozitiv

dacă a este negativ pe exact același

principiu Da Delta negativ nu intersectează

axa o x așa cum am lămurit mai

sus Da pe Delta egal cu 0 intersectează

într un singur punct pe turta mai

mari ca se intersectează în două

puncte și foarte important în toate

aceste trei cazuri pentru ca este

negativ nu ține apă Da este concavă

ce este important de văzut în acest

moment este că în toate aceste

trei cazuri discutate pe a pozitiv

respectiv trei cazuri prea negativ

vârful comentat în lecția precedentă

are coordonatele așa cum știam

x vârf igrec vârf Da x vârf igrec

vârf Da așa cum se vizualizează

aici în cazul în care Delta este

egal cu 0 x vârf este pe axa o

x și atunci el va coincide cu X1

și X2 rădăcinile egal confundate

ale funcției vorbind de situația

în care au este pozitiv orice valoare

am luat noi de pe grafic dacă mă

uit la ea va avea corespondent

pe axa o y o valoare pozitiv dacă

iau una de aici Da corespondență

pe axa o y o valoare pozitiv Nu

știu orice valoare repetă de pe

grafic corespondența va fi pe partea

pozitivă axa o y acesta este motiv

pentru care pot afirma în cazul

acesta că e ftx care așa cum știam

este este pozitiv Indiferent De

ce punct puneam iau de pe grafic

da în situația în care Delta este

egal cu 0 și aul este pozitiv la

fel orice punctaj luat de pe grafic

Da Și la și transmite la reprezentat

ca și coordonate praktik ordonata

punctelor de pe grafic este tot

pozitiv și în acest moment pot

să afirm că fdx care spunea mie

este este pozitiv dar în plus poate

fi și egal cu 0 și mai clar în

momentul în care vârful Da y10

taie 0 în cea de a treia situație

atunci când terta este pozitiv

în momentul în care luăm puncte

din interiorul rădăcinilor și le

Reprezentăm Da pe grafic Ele au

corespondență valoare negativă

adică partea aflată sub axa o x

Deci sub axa o x este parte negativă

care parte este sub axa o x ce

aflată aici Da și mai clar între

rădăcini în momentul în care vom

lua valori dinafară rădăcinilor

în momentul în care vor întâlni

graficul acestea vor fi pe partea

pozitivă a lui y și atunci în această

situație pot afirma Așa că dacă

x aparține lui x 1 x 2 Da deci

între rădăcini y este negativ adică

e Grecu nu uităm că este E de x

în caz contrar și mai clar când

x aparține lui minus infinit X1

Da reunit cu x 2 plus infinit în

afară Da X1 ăsta merge către minus

infinit Da sau minus infinit X1

respectiv X2 care merge către plus

infinit Da așa cum spuneam Deci

în afara rădăcinilor y cu va fi

pozitiv Deci se află spuneam graficul

deasupra axei o x pe x același

principiu Se poate purta discuția

și în cazul în care a ul este negativ

Adică dacă Delta este negativ așa

cum vedem nu intersectează axa

și lămurit acest aspect însă orice

puncte Aș vrea eu de pe grafic

în momentul în care le reprezint

pe axa o y Da le vor avea valori

negativ acesta este motiv pentru

care o să pot afirma fără discuții

că fdx care spuneam coincide cu

y y y va fi negativ în situația

în care Delta este egal cu 0 este

negativ Da vorbim de situația clară

în care orice punct aș lua de pe

grafic reprezentarea mă duce către

valori negative orice punctajul

Ăsta are un x să zică stai m Da

ăsta ar fi xemose stii Deci ym3

dacă aș lua punctul pe de exemplu

cu x p y p iar vin și spun x pe

o poate lua ce valori vreți dar

y Da este fără discuții negativ

singura situație ca și în cazul

celei prezentate yas-306 pentru

care în această situație pot afirma

că fdx la care egal cu y este mai

mic decât 0 că se află sub axa

dar și egal din cauza lui y p situația

3 atunci când Delta este pozitiv

exact aceeași discuție dacă luăm

puncte între rădăcini și le Reprezentăm

da pe grafic obținem să zic punctul

P de coordonate x pe y p y p are

valoare pozitiv dacă iau punctul

de aici zic de coordonate m de

coordonate x m y m de această dată

Da Și acesta este la fel pozitiv

iar vin și spun graficul pe distanța

asta X1 X2 se află deasupra axei

ceea ce îmi spune că aici va avea

valoare pozitiv atunci când luăm

elemente sau valori aflate în afara

rădăcinilor gen asta asta sau asta

nu știu să zic aici mă Păi da Va

întâlni graficul în punctul acesta

punct care a reprezentat prin prin

dar Care este negativ respectiv

punctul acesta care intersectează

graficul aici Și atunci el va avea

coordonată x y z și atunci concluzie

și în acest caz în această situație

atunci când x aparține X1 X2 Deci

când se află între rădăcini f de

x este Cum dacă se află deasupra

ții pozitiv Iar atunci când x aparține

lui minus aici minus infinit X1

ăsta este intervalul reunit cu

x 2 practic de aici încolo către

plus infinit Da X2 infinit atunci

graficul mă uit în afară este negativ

astfel în acest moment se poate

exprima semnul funcției de gradul

al doilea sub o formă mai clară

sub formă de tabel după cum Urmează

și anume atunci când a este pozitiv

cere trei situații clasice Delta

negativ Delta egal cu 0 Delta pozitiv

când Delta este negativ pe situația

de a pozitiv x ul nu are nici o

soluție reală trec pentru ca repetat

domeniul na existat un punct pe

care să îl pot reprezenta motiv

pentru care sau din care a rezultat

nouă că el este pozitiv de fiecare

dată Da y cu sau f de x în situația

în care Delta era negativ la fel

nu aveam punct pe care să le Prezintă

în domeniu pe x dar graficul funcției

se afla sub axei o x Praktiker

de instaura negativ și atunci pot

arăta asta și grafic pot arăta

asta și în tabel în cazul în care

te tai era egal cu 0 sunt situația

asta sau situația asta Atinge întru

singur punct punct care așa cum

ne am de murit este x vârf X1 sau

X2 toate cele trei coincide punct

în care e pixul este 0 și atunci

în cazul în care au e pozitiv ia

va avea valori doar pozitive aflate

deasupra axei o x în cazul în care

vorbim de ani stativ voi avea valori

negative și acum exprimam Aici

chiar și egal cu 0 situația lui

x Delta pozitiv X1 X2 două rădăcini

între acestea Cu siguranță se află

x vârf vârf are ca și corespondent

vârf deci practic vârful de coordonate

x vârf vârf Da abscisă ordonată

Și intru în caz și în celălalt

atunci când sunt între rădăcini

X1 X2 mă uit în cazul lui apozitiv

când sunt între rădăcini y este

negativ deci practic x este negativ

și vedeți că și vârf este sub axă

Da Acesta este motivul pentru care

am afirmat că e cu vârful între

rădăcini unde Clara de baloți de

0 erodat întreb de x negativ în

afara rădăcinilor pozitiv exact

pe același principiu Da între rădăcini

y V full vers care se vede Se vizualizează

este deasupra axei De ce este pozitiv

în X1 X2 funcție a evidenția valoarea

0 și atunci între rădăcini așa

cum afirmă e pozitiv se află deasupra

axei graficul în afara rădăcinilor

negativ adică în afara pe minus

infinit x 1 respectiv 2 plus infinit

mă aflu sub axa o x