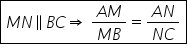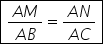Teorema lui Thales

tales din millet a fost un filozof

grec care a avut contribuții importante

în matematică și astronomie ala

calculat înălțimea piramidelor

din Egipt măsurând umbra acestora

pe nisip a determinat momentul

Din zi în care umbra era egală

cu înălțimea piramidei a demonstra

că unghiurile de la baza unui triunghi

isoscel sunt congruente a demonstra

că Unghiurile opuse la vârf sunt

congruente A descoperit constelația

Carului mic și a prezis o eclipsă

de soare și a demonstrat că o paralelă

dusă la una din Laturile unui triunghi

determina pe celelalte două laturi

segmente proporționale ultima pe

care o Vom numi teorema lui tales

o paralelă dusă la una din Laturile

unui triunghi determina pe celelalte

două laturi segmente proporționale

dacă avem un triunghi abc și am

dus MN o paralelă la latura b c

atunci a m supra MB va fi egal

cu a n supra n c nu face demonstrația

acestei teoreme și vom duce mai

întâi niște construcții ajutătoare

o să ducem o perpendiculară din

m pe latura AC și o perpendiculară

din n pe latura a b Fie m perpendiculară

pe AC și n f perpendiculară pe

ab în demonstrația acestei teoreme

vom folosi aria triunghiurilor

vă reamintesc că aria unui triunghi

în general se calculează după formula

baza ori înălțimea supra 2 ne propunem

să calculăm următorul rapport dintre

aria triunghiului amn și aria triunghiului

m b n unim punctele B și n aria

triunghiului a m n se poate scrie

ca produsul dintre latura a m ori

înălțimea corespunzătoare ei adică

n f supra 2 iar aria triunghiului

m b n la filatura m b înălțimea

corespunzătoare a n f supra 2 acesta

fiind un triunghi obtuzunghic înălțimea

din an este situată în exteriorul

triunghiului și aceasta este n

f b c aria triunghiului m b n se

poate scrie MB ori n supra 2 egal

mai departe cu a m ori n supra

2 ori 2 supra inverse amandoua

fracție n d a n s simplifica 2

cu 2 și m f și rămâne a m supra

MB am exprimat Așadar primul raport

din teorema lui tales trebuie Acum

se exprimă în raportul a n supra

n c pentru aceasta vom calcula

raportul ariilor triunghiurilor

a m n și m&c aria triunghiului

a m n supra aria triunghiului mnc

de data aceasta vom considera aria

triunghiului amn ca fiind latura

a n ori înălțimea corespunzătoare

a m e supra 2 a n ori m e supra

2 și aria triunghiului m n ce va

fi latura n c înălțimea corespunzătoare

ei adică m e supra 2 avem din o

fracție supraetajată vom înmulțit

prima fracție cu inversa celei

de a doua a n ori m a supra 2 ori

2 supra nc ori m n si simplifica

2 și m n și rămâne a n supra n

c am reușit să exprimăm și cel

de al doilea raport din teorema

lui tales acum Trebuie doar să

arătăm că aceste rapoarte sunt

egale mai exact va trebui să arătăm

că rapoartele ariilor acestor triunghiuri

sunt egale însă dacă ne uităm la

aceste rapoarte dintre ariile triunghiurilor

observăm că la numărător avem același

triunghi amn Deci mai trebuie doar

să arătăm că aria triunghiului

m b n va fi egală cu aria triunghiului

m n c ne propunem în continuare

Să arătăm că aria triunghiului

m d n este egală cu aria triunghiului

m n deocamdată vreo notă acestei

relații cu unu și doi vom încerca

să exprimăm ariile acestor triunghiuri

ducând alte înălțimi ale acestora

prelungim segmentul MN și ducem

b perpendiculară pe m n și c q

perpendicular pe m n Fie a b perpendiculară

pe m n și ce q perpendiculară pe

MN înseamnă că patrulaterul acesta

care se format pe b c q este un

dreptunghi pentru că acesta este

un paralelogram cu două unghiuri

drepte Deci e va fi dreptunghi

rezultă din această construcție

că pe b c q este dreptunghi intru

în dreptunghi Laturile opuse sunt

egale deci pe b va fi egală cu

qc acum vom exprima aria triunghiului

m b n ca fiind baza m n ori înălțimea

b p supra 2 și aria triunghiului

ce va fi exprimată ca produsul

dintre latura m n ori înălțimea

c q supra 2 având în vedere că

în formula ariilor acestor două

triunghiuri intervine același segment

m n și două înălțimi care sunt

egale va rezulta că ariile acestor

două triunghiuri vor fi egal voi

continua mai jos aria triunghiului

a m b n va fi egală cu produsul

dintre latura m n ori Înălțimea

pe b supra 2 aria triunghiului

mnc va fi m n ori q c supra 2 Dar

pe b și q c sunt egale înseamnă

că ariile acestor două triunghiuri

o fi egal aria triunghiului a m

b n va fi egală cu aria triunghiului

mnc și notez această relație cu

3 am arătat Așadar că rapoartele

ariilor acestor triunghiuri sunt

egale și atunci va rezulta că și

aceste segmente sunt proporționale

din relațiile 1 2 și 3 a rezultat

că teorema lui tales este demonstrată

din relația 1 doi și trei va rezulta

că a m supra MB este egal cu a

n supra Mc am demonstrat această

teoremă din aceasta egalitate de

rapoarte putem obține proporții

derivate Dacă adunăm numărătorii

la numitori obținem următoarea

relație a m supra a m plus MB a

fi egal cu a n supra a n plus m

c dar a m plus MB dacă ne uităm

pe figură a m plus MB va Fie segmentul

ab iar a n plus m c va fi segmentul

ac Deci obținem următoarea proporție

a m suprafa a b egal cu a n supra

AC în unele probleme vom folosi

această relație Deci e bine să

o reținem și pe aceasta am demonstrat

Așadar că o paralelă la una din

Laturile unui triunghi formează

segmente proporționale a m supra

m b va fi egal cu a n supra n c

teorema lui Thales este adevărată

și în cazul în care paralela este

dusă în exteriorul triunghiului

și am obținut de asemenea prin

proporții derivate următoarea relație

a m supra ab egal cu a n supra

AC în continuare o să facem o problemă

în triunghiul m n p se consideră

punctul E situat pe latura m n

și F situat pe latura n p astfel

încât ef să fie paralel cu m p

știind că m este egal cu 6 m n

egal cu 16 și este egal cu 18 cm

Calculați n e n s și NP demonstrație

bombe aplica teorema lui talles

având în vedere că e f este paralelă

cu mp din teorema lui tales va

rezulta următoarea relație n supra

m egal cu n e supra SP nu se cunoaște

segmentul n m Dar putem să îl aflăm

și făcând diferența dintre segmentele

n m și i m n e este egal cu n m

minus e m egal cu 16 minus 6 și

egal cu 10 cm în egalitatea de

mai sus 10 supra Emi este 6 egal

cu n supra 18 din această relație

îl aflăm pe an acesta este egal

cu 10 ori 18 supra șase se simplifică

18 cu șase și rămâne trei obținem

10 ori 3 egal cu 30 cm Și mai trebuie

să dau lemn pe n p NP va fi suma

dintre segmentele an și este egal

cu 30 plus 18 egal cu 48 cm