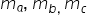Teorema medianei

în acest clip o să discutăm despre

teorema medianei aceasta ne permite

să calculăm lungimea medianei În

triunghiul oarecare atunci când

se cunosc lungimile laturilor acestuia

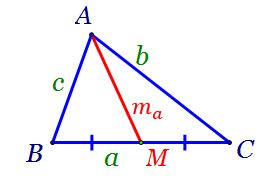
avem triunghiul oarecare abc și

am notat laturile acestuia cu a

mic b mic respectiv c mic vom nota

cu m indice A lungimea medianei

corespunzătoare laturii a mic cu

m indice b notăm mediană corespunzătoare

laturii b mic și cu MC medianei

corespunzătoare laturii c au loc

următoarele relații m a la pătrat

este egal cu 2 pe lângă b pătrat

plus c pătrat minus a pătrat supra

4 m b la pătrat este egal cu 2

pe lângă a pătrat plus pătrat minus

b pătrat supra 4 iar mediană corespunzătoare

laturii c la pătrat va fi egală

cu 2 pe lângă a pătrat plus b pătrat

minus c p supra 4 vom demonstra

prima relație celelalte două demonstrând

USA analog dacă a m este mediană

atunci are loc următoarea relație

vectorială a m este semisuma vectorilor

ab și ac Acest lucru se poate demonstra

foarte ușor dacă prelungim mediana

a m cu un segment având aceeași

lungime cu a m atunci se obține

un paralelogram diagonala acestui

paralelogram este suma vectorilor

ab și ac prin urmare a m va fi

jumătate din ab plus AC din această

relație rezultă că 2 a m este egal

cu ab plus AC ridicăm la pătrat

aceasta egalitate și obținem 4

m la pătrat egal cu ab plus AC

la pătrat egal în continuare cu

AB la pătrat plus 2ab ori AC plus

a ce la pătrat mediană a m sau

notat cu m indice a prin urmare

patru ori m indice a la pătrat

va fi egal în loc de ape putem

scrie Ce mic în loc de ace avem

de mic plus doi ori produsul scalar

AB AC este egal cu modul de a b

ori modul de a c ori cosinusul

unghiului dintre cei doi vectori

prin urmare aici voi Scrie si ori

b ori cosinus de ei în continuare

aplicăm teorema cosinusului cosinus

de am este egal cu b pătrat plus

si pătrat minus a pătrat supra

2 b c și atunci din aceste două

relații obținem următoarea formulă

4m a pătrat egal cu c pătrat plus

b pătrat plus 2 b c iar un loc

de cosinus de a vă scrie relația

de mai jos b pătrat plus c pătrat

minus a pătrat supra 2 b c se simplifică

2bc și avem 4 m a la pătrat egal

b pătrat cu b pătrat este 2 b pătrat

apoi urmează 2 si pătrat minus

a pătrat 4 m pătrat va fi egal

cu 2 pe lângă b pătrat plus c pătrat

minus a pătrat iar de aici exprimând

m a la pătrat se obține 2 pe lângă

b pătrat plus c pătrat minus a

pătrat supra 4 am demonstrat prima

formulă din teorema medianei celelalt

de formule se demonstrează în mod

asemănător în continuare Haideți

să facem un exercițiu Se dă triunghiul

abc unde ab are lungimea egală

cu șapte unități AC are lungimea

egală cu trei unități b c este

egal cu 5 unități c m este mediană

și se cere să calculăm lungimea

segmentului cm aplicăm teorema

medianei cm la pătrat va fi egal

cu 2 pe lângă AC la pătrat plus

bc la pătrat minus a b la pătrat

totul supra 4 cm la pătrat va fi

egal cu 2 pe lângă 3 la a doua

plus 5 la a doua minus 7 la a doua

totul supra 4 egal cu 2 ori 9 plus

25 este 34 minus 49 totul supra

4 egal 234 este 68 minus 49 este

egal cu 19 supra 4 prin urmare

ce an va fi egal cu radical din

19 supra 2