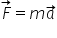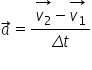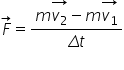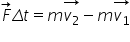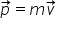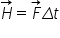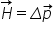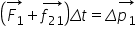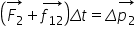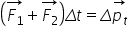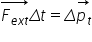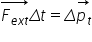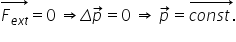Teorema variaţiei impulsului. Legea de conservare a impulsului.
Tag-uri
Partajeaza in Google Classroom

Transcript
încet de 5-a lecție despre legi
de conservare în mecanică vom introduce
noțiunea de Impuls și vom discuta
despre legea de conservare a impulsului
1 să introducem noțiunea de impulsul
forței notată cu h care e definită
ca produsul dintre Forța F ce acționează
asupra unui corp și intervalul
de timp Delta t în care această
forță acționează în datorită ecuații
fundamentale a dinamicii forța
poate fi scrisă ca produsul dintre
masă și accelerație accelerație
este la rândul ei definită în cinematică
ca variația vectorului viteză în
raport cu intervalul de timp în
care se produce această variație
rezultă că putem scrie impulsul
forței H ca fiind m masa înmulțită
cu variația vitezei sau mai putem
grupa acești termeni și scrie că
h este egală cu variația produsului
dintre masă și viteză pentru că
masa corpului nu variază în timp
deci ma să o putem pune atât în
interiorul variației cât și în
exterior fiind o constat numai
viteza V variază în timp deci avem
o relație intermediară pentru impulsul
forței utilitatea practică a impulsului
forței vine din faptul că forța
uneori nu poate fi măsurată în
special atunci când ea ținea de
un interval Delta t de timp foarte
scurt în Spre exemplu în ciocnirea
bilelor de biliard ia are loc aproape
instantaneu și Deci acțiunea forței
de interacțiune în timpul ciocnirii
bilelor se petrece intru în timp
Delta t foarte mic și Este dificil
din acest din această cauză să
se măsoare forța exercitată la
ciocnire dar masele și vitezele
bilelor atât înainte cât și după
ciocnire sunt ușor de măsurat Deci
acest produs mor V este mai ușor
de măsurat în acest caz și în concluzie
în aplicații practice impulsul
forței e mai ușor de folosit decât
forța în sine introducem impulsul
unei unui corp ca fiind acest produs
dintre masă și viteză de impulsul
unui corp se notează cu perii este
un Vector și definit ca produsul
dintre masa corpului și viteza
lui V rezultă imediat teorema variației
impulsului și anume variația impulsului
unui corp este egală cu impulsul
forței aplicate corpului de această
ecuație sau teoremă rezultă direct
din formula echivalentă pentru
impulsul forței aceasta și definiție
în plus Delta p este egal cu h
o o formulă alternativă pentru
aceeași teoremă variației impulsului
este aceea Că Forța f este egală
cu variația impulsului corpului
în unitatea de timp Folosind definiția
impulsului forței în prima forma
a teoremei variației impulsului
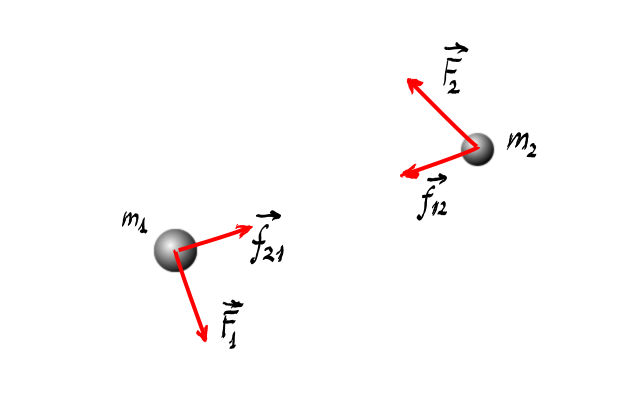
impulsul unui sistem de corpuri
Considerăm două corpuri meci avem
corpul si unul și corpul si doi
între ele existând o pereche de
forțe Deci oi în două forțe de
interacțiune notate cu f21 smyk
2 1 care este forța de acțiune
a corpului 2 asupra corpului 1
și cealaltă forță din interacțiune
este F12 Care este reacțiunea la
f21 și este forța de interacțiune
a corpului 1 asupra corpului 2
de asemeni în acest sistem de corpuri
există forțe externe pe care îl
notăm cu F 1 în cazul corpului
1 Deci asupra corpului 1 acționează
o forță externe F1 și asupra corpului
2 acționează o o altă forță notată
cu doi tot o forță externe forțele
externe au orientări și magnitudini
arbitrare putem scrie teorema variației
impulsului pentru primul corp Deci
teoremă variației impulsului pentru
ce unu se scrie așa F1 plus smyk
doi unu înmulțit cu Delta t este
egal cu variația impulsului corpului
1 m 1 înmulțit cu v pentru corpul
C2 se scrie ca F2 forța externă
S2 Plus forța intern F12 înmulțită
cu Delta t egal cu variația impulsului
corpului Doi vecini 2 v-2 acum
deoarece forțele f21 și F12 sunt
interacțiuni interne ale sistemului
ele vor fi egale și de semn opus
de avem următoarei ecuații F12
Vector bineînțeles este egal cu
minus f21 de asemeni introducem
forța rezultantă a tuturor forțelor
externe de ce notăm cu F suma dintre
F1 și F2 Deci f este rezultanta
forțelor externe ce acționează
asupra corpurilor din sistem din
aceste ecuații și din ecuațiile
provenite din teoremă variației
impulsului putem scrie că putem
face suma deci putem scrie că F1
plus F2 1 plus F2 plus smyk 1.2
înmulțit cu Delta t este egal cu
Delta m101 Plus m 2 v-2 Dar suma
dintre s21 și F12 este 0 Deci când
adunăm aceste două forțe obținem
0 iar suma dintre F1 și F2 este
forța rezultantă de ce avem că
f ori Delta t este egal cu Delta
m 1 v-1 plus m 2 v-2 în consecință
dacă notăm cu p impulsul total
al sistemului definit ca pe 1 plus
pe 2 suma impulsurilor celor două
corpuri 10 egal cu 1 v-1 plus m
2 v-2 obținem că forța rezultantă
înmulțită cu Delta t este egală
cu variația impulsului total Deci
întrun sistem de corpuri recuperăm
teoremă variației impulsului pentru
impulsul total și forța totală
externă asupra sistemului Deci
forța externă rezultantă înmulțită
cu Delta t este variația impulsului
total al sistemului și acum ajungem
la Legea conservării impulsului
care spune că dacă rezultanta forțelor
externe pe care tocmai am văzut
o este nulă atunci impulsul total
al sistemului este constant de
se conservă iar a o porno foarte
simplă și anume că exact cum am
spus forța totală în rezultantă
a forțelor externe este egal cu
0 implică că impulsul total suma
tuturor vectorilor Impuls de Impuls
ale corpurilor din sistem este
constant sau variația lui este
0 este o lege care arată foarte
simplu este foarte simplă dar are
multe aplicații practice Spre exemplu
obținem propagarea mișcarea oricărui
avion sau rachetă cu motor Deci
nu ne referim aici la un planor
sau ceva de genul ăsta dar un avion
cu motoare sau cu motor se propagă
exact datorită legii conservării
impulsului și anume jetul de gaz
injectat de către motoare care
are un un Impuls să notăm cu p
j de la jet de gaz va fi egal datorită
legii conservării impulsului cu
impulsul avionului deci pe a este
egal cu minus pe pe Jay de la Jet
Deci propagarea avionului mișcarea
lui facem exact prin acest aspect
și anume motoarele injectează cu
viteză mare cu Impuls foarte mare
aceste gaze și prin legea conservării
impulsului avionul sau racheta
va primi la rândul său o un un
Impuls de sens contrar Deci înainte
același efectul vedem Spre exemplu
un reculul unei arme ceea ce vedem
în această a doua imagine este
un pic care trage un glonț un glonț
glonte este trimis cu viteză mare
în vitrină direcția înainte de
ce aceasta este impulsul glonte
lui își atunci datorită legii conservării
impulsului arma va avea un recul
în direcția opusă Deci aceasta
va fi impulsul pistolului bineînțeles
impulsul pistolului este egal și
de sens opus cu impulsul glonte
ca să facem un scurt exercițiu
Să presupunem că avem un caz tipic
ca de exemplu masa pistolului este
jumătate de kilogram Masa glonte
lui care de obicei mult mai mică
o luăm 5 g și viteza glonțului
care tipică ceva de genul 400 de
metri pe secundă din legea de conservare
a impulsului obținem că masa pistoli
Makita cu viteza pistolului este
egală cu masa glontului înmulțită
cu viteza glonțului această ecuație
sau obținut din proiectarea pe
o axă o x De ce alegem o axă OLX
paralelă cu Axa pistolului pe care
proiectăm ecuația vectorială și
obținem această ecuație între Maria
magnitudine vectorilor și mase
Deci obține încă viteza pistolului
este egală cu masa glonte lui împărțită
la masa pistol înmulțită cu viteza
glonțului folosind acele valori
pe care le am luat obținem că viteza
de regula pistolului este egală
cu masa glonte lui Adică cinci
ori 10 la minus 3 kilograme împărțit
la masa pistolului Care este 5
ori 10 la minus 1 kg notație științifică
aceasta 10 la mine folosită aici
ca 10 la minus 30 la minus unu
a fost explicată în prima lege
de cinematică înmulțită cu viteza
pistolului Care este 400 de metri
pe secunda 10 obținem 5 cu 5 se
găsesc simplifică 10 la minus 1
devine 10 la plus 1 la dus la numitor
Deci avem 10 la minus doi munți
cu 400 ce obținem o viteză de recul
a pistolului de 4 m pe secundă
Care este o viteză semnificativă
motiv pentru care cineva care ține
în mână pistolul și execută aceasta
tragere va simții această forță
sau ce stim puls