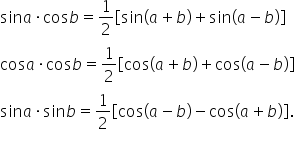Tranformarea produselor în sume

în unele exerciții este mai convenabil

să transformăm produsele de funcții

trigonometrice în sume în acest

clip ne propunem să găsim formulele

pentru sinus de aur cosinus de

B cosinus de a ori cosinus de b

și sinus de a ori sinus de b Am

pornit de la aceste două formule

sinusul sumei respectiv sinusul

diferenței adunăm relațiile 1 și

2 și vom obține ținuți de a plus

b plus sinus de a minus b egal

cu 2 sinus de cosinus de b Deci

sinus de a ori cosinus de B va

fi egal cu 1 supra 2 pe lângă sinus

de a plus b plus sinus de a minus

b am găsit prima formula de transformare

a produsului în sumă pentru a transforma

în suma produsul cos de aur coș

de B pornind de la aceste două

relații pe care le însuma adunând

relațiile 1 și 2 obținem cosinus

de a plus b plus cosinus de a minus

b egal cu 2 cos de a cos de b prin

urmare cosinus de aur cosinus de

B este egal cu 1 supra 2 pe lângă

cosinus de a plus b plus cosinus

de a minus b Dacă scădem relațiile

1 și 2 vom avea cosinus de a minus

b minus cosinus de a plus b egal

cu 2 sinus de a sinus de b prin

urmare sinus de a ori sinus de

B este egal cu 1 supra 2 pe lângă

cosinus de a minus b minus cosinus

de a plus b acestea sunt cele trei

formule de transformare a produselor

în sume iar în continuare Haideți

să facem câteva exerciții am rescris

cele trei formule și un prim exercițiu

Haide să transformăm în sumă următorul

produs cosinus de 4 Alfa ori cosinus

de Alfa aplicăm a doua formulăm

și avem 1 pe 2 pe lângă cosinus

de a plus b în acest caz a este

4 Alfa iar b este 2 Alfa Deci avem

cosinus de 4 Alpha plus 2 Alfa

plus cosinus de 4 Alpha minus 2

L fam egal cu 1 pe 2 pe lângă cosinus

de 6 l fă plus cosinus de 2 Alfa

următorul exercițiu se cere să

transformăm în suma produsul sinus

de 35 de grade ori cosinus de 25

de grade Aplicând formula sinus

de a ori cosinus de b și avem unul

pe 2 pe lângă sinus de 35 de grade

plus 25 plus sinus de 35 de grade

minus 25 egal cu 1 pe 2 pe lângă

sinus de 60 de grade plus sinus

de 10 grade egal cu 1 pe 2 pe lângă

sin de 60 este radical din 3 pe

2 iar sinus de 10 grade Rămâne

așa și egal cu radical din 3 supra

4 plus 1 pe 2 ori sinus de 10 grade

și ultimul exercițiu se cere să

scriem sub forma unei sume următorul

produs 2 sinus de 50 de grade ori

cosinus de 50 de grade ori sinus

de 70 de grade dacă ne uităm la

primii trei factori putem recunoaște

o formulă vă reamintesc formula

pentru sinus sul argumentului dublu

sinus de 2x este egal cu 2 sinus

de x cosinus de x Așadar dacă ne

uităm la primii trei factori 2

sinus de 50 ori cosinus de 50 va

fi egal cu sinus de 2 ori 50 prin

urmare aici vom avea sinus de 100

de grade Deci avem sinus de 100

de grade ori sinus de 70 și acum

putem să aplicăm ultima formulăm

și vom avea 1 pe 2 pe lângă cosinus

de 100 de grade minus 70 minus

cosinus de 100 plus 70 egal cu

1 pe 2 pe lângă cosinus de 30 de

grade minus cosinus de 170 de grade

egal cu 1 pe 2 pe lângă cos de

30 este radical din 3 pe 2 iar

cosinus de 170 Rămâne așa și egal

cu radical din 3 supra 4 minus

1 pe 2 ori cosinus de 170 de grade