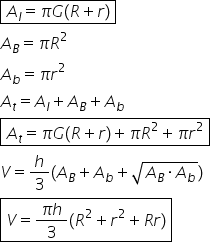Trunchiul de con circular drept (aplicații)

să aplicăm formule de pe care le

am învățat pentru trunchiul de

con circular drept și ni se dă

această problemă un trunchi de

con circular drept are raza bazei

mici de 2 cm raza bazei mari de

8 cm și generatoarea de 10 cm Să

găsim aria laterală aria totală

și volumul trunchiului de con prin

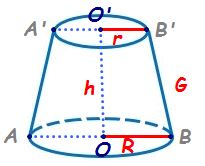
urmare voi nota aici cu o prim

centrul bazei mici notăm și cu

o centrul bazei mari și să Reprezentăm

acum razele avem aici raza bazei

mari raza bazei mici și să le și

notăm avem aici aer mic aer mare

mai cunoaștem că generatoarea este

de 10 cm și să găsim aria laterală

aria totală și volumul trunchiului

de con pentru început să scrie

în formula pentru aria laterală

aria laterală a unui trunchi de

con este egală cu Orange înmulțit

cu deschidem paranteza R mic plus

R Mare acum știm și generatoarea

și timp și valorile celor două

raze deci putem să calculăm va

rezulta trecem aici că aria laterală

este egală cu pi pi înmulțit cu

g este 10 pe lângă avem aici și

rază mică plus raza mare 2 plus

8 și obținem 10 ore 10 adică 100

pi centimetri pătrați pentru aria

totală avem formula aria laterală

adunată cu ariile celor două baze

adică fii orar mare la pătrat plus

spion aer mic la pătrat rezultă

aria totală egală cu aria laterală

100 Picu avem aici urma are la

pătrat adică 8 la a doua 64 fi

adunat cu aer mic la a doua adică

2 la a doua 4 ori avem 64 cu 468

cu 100 168 Pi cm pătrați pentru

volum trece în formula volumului

egal cu pi înmulțit cu h supra

3 Unde este înălțimea trunchiului

de con UV am trasat și pe desen

pe lângă aer mare la a doua plus

ceramic la a doua plus produsul

dintre armare și R mic și să trasăm

acum înălțimea adică oprim o Păi

avem valoarea lui Iair mare și

lui hernic ne mai trebuie însă

să determinăm înălțimea adică lungimea

segmentului oprim o Cum facem acest

lucru Păi putem să lucrăm În trapezul

dreptunghic o a a prim o prim și

chiar o să luăm separat Iată o

a a prim o prim avem aici Roz Da

Mică să trecem și valoarea Avem

doi centimetri Raza bazei mici

și raza bazei mari o Adi 8 cm și

mai știm că avem aici 10 cm noi

vrem să găsim lungimea segmentului

oprim o Cum facem acest lucru având

în vedere că avem aici un trapez

dreptunghic pe cred că deja baza

obișnuit cu asemenea probleme deja

din clasa a șaptea construim perpendiculara

din A prim pe o a și trecem aici

că avem punctul m și acest unghi

are 90 de grade Deci voi scrie

aici ducem a prim m perpendicular

pe A păi ce o să rezulte din această

relație din această construcție

de fapt ce fel de patrulater este

acesta om a prim o prim pe avem

de fapt un dreptunghi Iată o prim

o este paralelă cu a prim m notăm

rezultă de aici că o prim o paralelă

cu a prim m știm din construcția

din definiția trapezului că o prim

a prim Cum este paralelă cu o ei

adică cu o e și mai avem și măsura

unghiului o sau măsura acestui

unghi nu are importanță de 90 de

grade cu alte cuvinte ce obținem

Aici este un dreptunghi de Ce rezultă

că o a prim o prim este dreptunghi

Păi din această relație rezultă

două lucruri foarte important și

anume Deci rezultă de aici pe de

o parte avem că lungimea segmentului

o prim o este egală cu lungimea

segmentului a prim m Deci o prim

o egal cu a prim m și mai avem

și faptul că o prim a este egal

cu o m o prim a a prim a prim pardon

egal cu o m egal prin urmare cu

2 cm și chiar o să trec aici că

avem Iată 2 cm reprezintă om pe

Acum putem foarte simplu foarte

ușor să determinăm valoarea segmentul

lungimea segmentului m a și anume

8 minus doi adică 6 și o să șterg

aici Deci să notăm că m a egal

cu o A deci o A minus om cu alte

cuvinte opt minus 2 Deci 6 cm De

ce ne interesează și lungimea acestui

segment iată că am obținut aici

triunghiul dreptunghic a prim m

a știm lungimea ipotenuzei știm

lungimea acestei catete deci putem

să găsim lungimea segmentului a

prim m Care este congruent cu o

prim o și am determinat înălțimea

Deci în triunghiul a prim m a cu

măsura unghiului m de 90 de grade

aplicăm teorema lui Pitagora de

Ce rezultă din teorema lui Pitagora

si vom avea a prim m la pătrat

egal cu a prim a la pătrat minus

ma la pătrat și să facem calculul

vom avea așa că a prim m la pătrat

este egal cu avem aici 10 la a

doua de cos minus 6 la a doua 36

ne dă 64 de unde rezultă că a prim

m are lungimea de 8 cm 12 m aici

că avem 8 cm din această relație

Iată avem aici o prim m egal cu

a m o să trag relația 1 Deci rezultă

din relația 1 că chiar o să scriu

tot cu roșu oprim o egal și el

tot cu 8 cm din aceste două relații

at relația 1 trec aici relația

2 deci din 1 și 2 rezultă lungimea

segmentului oprim o trecem aici

8 cm și acum Revenim la calculul

volumului trunchiului le putem

să ștergem aici și vom calcula

volumul este egal cu pi înmulțit

cu h supra 3 Păi am găsit că are

valoarea de 8 cm și trecem 8 Deci

vom avea 8 supra 3 pe lângă urma

are la pătrat 64 plus R mic la

pătrat adică 2 la a doua Deci 4

plus urma are o Rednic copter 216

avem aici 20 cu 6484 Deci pai ori

8 supra 3 înmulțit cu 84 putem

să simplificăm prin trei ne rămâne

aici și 28 ce facem calculul 8

ori 28 ne dă 224 pi centimetri

cubi și am de terminat astfel și

volumul acestui trunchi de con