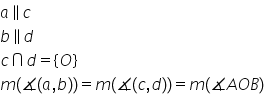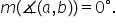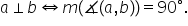Unghiul a două drepte în spațiu

în această secvență vom învăța

despre unghiul făcut de două drepte

în spațiu și cred că presupuneți

deja că avem două situații și anume

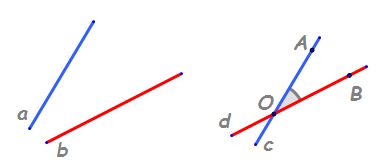
prima situație în care dreptele

sunt drepte coplanare și aici putem

întâlnii drepte concurente cele

două drepte au un singur punct

în comun și Haide să trecem ca

avem aici patru unghiuri unui unghi

al doilea unghi și aceste două

unghiuri acestea două sunt congruente

la fel și acesteia două Prin urmare

avem doar două măsuri de unghiuri

o măsură și încă una și am spus

că o vom alege pe cea mai mică

Deci Considerăm că măsura unghiului

făcut de dreptele a și b este măsura

unghiului dar nu tot aici o și

aici vom trece 1 Deci unghiul o1

un Dacă dreptele sunt paralele

atunci e chiar foarte simplu măsura

unghiului făcut de două drepte

paralele are 0 grade situația interesantă

este următoarea când dreptele sunt

necoplanare Iată dreapta este inclusă

în plan iar dreapta b este inclusă

într un alt plan Două drepte necoplanare

nu formează concret un unghi pentru

că ele nu au niciun punct în comun

însă putem să stabilim înclinarea

unei drepte față de cealaltă chiar

și în această situație cum vom

proceda printr un punct al spațiului

de exemplu prin acest punct vom

construi câte o paralelă la fiecare

din cele două drepte Deci prin

punctul P ducem o paralelă la dreapta

a și cel mai bine ar fi să o trasați

folosind de ori că aceasta este

a prim a prim și a sunt drepte

paralele și tot prin punctul P

vom duce o paralelă la dreapta

d mic bun să construim și această

paralelă și notăm aici B prim prin

definiție Considerăm că măsura

unghiului făcut de dreptele a și

b este măsura unghiului făcut de

paralelele acestor drept aduce

prin același punct al spațiului

și avem aici a prim și B prim și

avem prin urmare definiția măsura

unghiului a două drepte necoplanare

este măsura unghiului format de

paralelele acestora duce prin același

punct al spațiului și să notăm

că a este paralelă cu a prim și

b este paralelă cu b prim Credeți

că are importanță Unde în spațiu

în alege în punctul prin care ducem

paralelele la cele două drepte

Păi dacă alegem de exemplu un alt

punct să spunem că alegem aici

punct m și vrem să ducem prin acest

punct paralele la dreapta a și

la dreapta b duce mai întâi paralelă

la dreapta a bun este aceasta și

apoi construim o paralelă la dreapta

d prin același punct M pardon trebuie

să o așezăm diferit și să le notăm

avem aici b secunde și aici notăm

că avem a second măsura unghiului

făcut de aceste două drepte este

diferită de măsura unghiului făcut

de aceste două drepte adică măsura

acestui unghi e diferită de măsura

acestui unghi nu pentru că cele

două unghiuri au laturile respectiv

paralele devreme si a secund este

paralelă cu a și a este paralelă

cu a prim înseamnă că a prim și

a second sunt drepte paralele la

fel B prim paralel cu b secunde

poate cuvinte aceste două unghiuri

acesta și acesta sunt unghiuri

concurente Deci nu contează Unde

în spațiu ne alegem punctul prin

care construim cele două drepte

paralele cu dreptele necoplanare

în practică în exerciții vom proceda

în felul următor ca să determinăm

unghiul făcut de dreptele necoplanare

a și b vom considera pe una din

cele două drepte un punct și să

alegem aici punctul P prin acest

punct vom construi o paralelă la

cealaltă dreaptă adică la dreapta

a și să construim o paralelă la

dreapta a și o Vom nota a prim

Deci trecem aici a prim paralelă

cu A atunci conform definiției

Ce rezultă că măsura unghiului

făcut de dreptele necoplanare a

și b este egală cu măsura unghiului

făcut de aceste drepte a prim care

este paralelă cu a și nu mai avem

aici o paralelă pentru dreapta

BC Avem chiar dreapta b d și măsura

unghiului făcut de dreptele a prim

și b în continuare să facem și

o aplicație și mi se dă cubul ABCD

a prim b prim c prim D prim și

vrem să determinăm măsura unghiului

făcut de dreptele a b și b prim

c prim Deci avem dreapta AB o trasatura

b prim c prim e clar că aceste

două drepte sunt drepte necoplanare

Deci ca să determinăm unghiul făcut

măsura unghiului făcut de ele Le

alegem un punct pe una din cele

două drepte să ne alegem de exemplu

un punct pe dreapta ab și cel mai

bine ar fi să ne alegem un punct

deja este dat Deci fie a fie b

apoi prin punctul ales trebuie

să ducem o paralelă la dreapta

b prim c prim și paralela respectivă

trebuie să intersecteze dreapta

AB Păi putem să ne alegem oricare

din cele două puncte a și b însă

eu zic că e mai simplu să alegem

punctul B pentru că ea e ușor de

văzut că dreapta b prim c prim

este paralelă cu dreapta BC și

dreptele BC și ab se intersectează

de ceai de să notăm că b prim c

prim este paralelă cu bc prin urmare

măsura unghiului făcut de dreptele

necoplanare a b și b prim c prim

este egală cu măsura cărui unghi

pe avem unghiul făcut de dreptele

a b și b c în loc de dreapta b

prim c prim Boema dreapta BC Deci

avem de fapt ce unghi măsura unghiului

abc care Câte grade are Păi având

aici un pătrat ABCD înseamnă că

avem 90 de grade BC egal mai departe

cu 90 de grade altă întrebare să

determinăm acum măsura unghiului

făcut de dreptele a d prim deci

a d prim voi șterge aici ca să

ne fie mai ușor deci Avem așa a

d prim și b c trecem aici b c și

în această situație avem tot drepte

necoplanare prin urmare Trebuie

să ducem la una din cele două drepte

O dreaptă paralelă care să intersecteze

cealaltă dreaptă și ușor de văzut

că dreapta BC este paralelă cu

ad și dreapta a d intersectează

setează dreapta a d prim cu alte

cuvinte unghiul pe care îl vom

obține este acesta acest unghi

de ceai de să notăm că bc este

paralelă cu ad bc paralelă cu ad

prin urmare măsura unghiului făcut

de dreptele necoplanare a d prim

și BC este egală cu măsura cărui

unghi Păi ne rămâne ad prim și

iată dreapta BC a fost înlocuită

cu dreapta ad Deci trecem aici

ad prim și a d adică unghiul D

prim a d măsura unghiului D prim

a d Câte grade are acest unghi

având aici un pătrat a d d prim

a prim Este pătrat a d prim Este

diagonala în pătrat AD este latura

de cea bem 45 de grade ident că

aceasta nu era singura modalitate

de determinare a măsurii unghiului

făcut de aceste două drepte necoplanare

puteam să Considerăm De exemplu

a prim D prim paralel cu b c sau

puteam să construim b c prim paralelă

cu chiar să o construiesc b c prim

Iată paralelă cu a d prim și atunci

am fi avut acest unghi care are

și el Evident tot 45 de grade ultima

întrebare să găsim măsura unghiului

făcut de dreptele b c prim bc prim

de această dreaptă și a prim D

Ia să vedem a prinde și acestei

drepte sunt drepte necoplanare

si paralelă să construim iar paralela

respectivă să intersecteze cealaltă

dreaptă Păi putem Să considerăm

de exemplu b prim c care este paralelă

cu dreapta a prim D practică aici

am construit o paralelă prin punctul

de intersecție al diagonalelor

acestui pătrat b c c prim D prim

avem aici punctul O punctul de

intersecție al acestora diagonale

deci putem să notăm că a prim d

este paralelă cu b prim c prin

urmare măsura unghiului făcut de

dreptele b c prim și a prim d este

egală cu măsura unghiului făcute

dreptele b c prim și a prim de

a fost înlocuită cu b prim c b

prim c adică e vorba de măsura

acestui unghi măsura unghiului

avem B prim o b toate unghiurile

sunt congruente pentru că diagonalele

b c prim și b prim c sunt perpendiculare

deci putem să alegem oricare din

cele patru unghiuri b prin o b

de exemplu egal cu 90 de grade

și sa încheiat