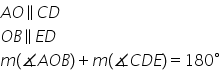Unghiuri cu laturile respectiv paralele
Tag-uri
Partajeaza in Google Classroom

Transcript
Cum sunt două unghiuri cu laturile
respectiv paralele dacă ni se dă
un unghi de exemplu acesta chiar
am trecut aici Vârful cu 1 Deci
avem unghiul numărul unu și vrem
să construim un alt unghi cu laturile
paralele cu laturile acestui unghi
pe a d se duce o paralelă la această
latură Iată am trasat om și acum
vrem să ducem o paralelă la această
latură însă mai întâi Ce avem de
stabilit trebuie să stabilim unde
va fi vârful unghiului Deci care
va fi originea semidreptelor ce
avem două posibilități fie alegem
ca originea semidreptelor să fie
aceasta și aceasta dacă alegem
Prima variantă Deci ducem dreapta
Paralelă la această latură prin
acest punct Iată vom obține acest
unghi și să îl notăm cu 2-a bine
aceste două unghiuri au laturile
respectiv paralele pentru că această
latură paralelă cu aceasta și aceasta
este paralelă cu aceasta cele două
unghiuri unghiul 1 și unghiul 2
să știți că sunt unghiuri congruente
dacă însă vom lua doua am situație
în care alegem ca originea semidreptelor
să fie aceasta atunci Deci duce
mai întâi o paralelă la această
latură Iată și apoi aici ducem
o paralelă la această latură prin
acest punct și am obținut acum
un alt unghi o să trec aici unghiul
numărul 3 Eh este două unghiuri
acesta și acesta au laturile respectiv
paralele însă acesta este un unghi
ascuțit și acesta este un unghi
obtuz în această situație cele
două unghiuri sunt suplementare
Deci trecem că măsura unghiului
1 adunată cu măsura unghiului este
egală cu 180 de grade prin urmare
avem de fapt două posibilități
când vorbim de unghiuri cu laturile
respectiv paralele ele sunt fie
congruente Cum a fost aici fie
sunt suplementare Deci avem de
fapt teoremă două unghiuri cu laturile
respectiv paralele sunt congruente
sau suplementare nu vom demonstra
această teoremă se importantă o
reține și mai ales să reținem faptul
că această teoremă are loc și situația
în care unghiurile se află în plane
diferite iată în planul alfa avem
acest unghi unghiul notat tot cu
numărul 1 iar în planul Beta avem
acestu cele două unghiuri au laturile
respectiv paralele chiar dacă ele
sunt în plane diferite această
latură paralelă cu aceasta Iar
aceasta este paralelă cu aceasta
in aceasta situație cele două unghiuri
sunt congruente la fel se întâmplă
și dacă avem un alt plan care conține
un ghiul notat aici 3 care are
laturile respectiv paralele cu
acest unghi însă avem aici un unghi
obtuz aici unul ascuțit înseamnă
că cele două unghiuri sunt suplementare
în continuare vreau să discutăm
puțin despre unghiul făcut de două
drepte concurente Câte unghiuri
formează aceste două drepte concurente
Păi avem patru unghiuri Iar avem
aici un unghi trecem numărul unu
avem aici un alt unghi trecem 2
Mai avem încă un unghi aici și
Mai avem încă unul aici Cum sunt
aceste unghiuri Păi unghiul numărul
1 este congruent cu unghiul numărul
3 pentru că sunt unghiuri opuse
la vârf d sunt unghiuri opuse la
vârf unghiul nu numărul 2 este
congruent cu unghiul numărul 4
din aceeași cauză sunt unghiuri
opuse la vârf cu alte cuvinte Avem
doar două măsuri de unghiuri pentru
că aceste două unghiuri sunt congruente
la fel și acestea acum ca să stabilim
înclinarea unei drepte față de
cealaltă este suficient să Considerăm
o singură măsură și o vom alege
pe cea mai mică Aceasta este o
convenție cu alte cuvinte măsura
unghiului făcut de dreptele a b
este egală cu măsura unghiului
aici avem un unghi obtuz aici un
unghi ascuțit de circa alege pe
acesta putem să trecem unghiul
numărul 2 sau unghiul numărul 4
ele sunt congruente Deci măsura
unghiului făcut de aceste două
drepte este dată de măsura acestui
unghi Evident Dacă dreptele erau
pe prind culare atunci toate unghiurile
ar fi fost congruente fiecare având
măsura egală cu 90 de grade acum
Haideți să ne uităm puțin la acest
desen în acest plan Avem două drepte
concurente a și b și nici se dă
încă un plan în care avem tot așa
două drepte concurente c și d care
au această proprietate dreapta
a este paralela cu dreapta c iar
dreapta d este paralelă cu dreapta
d exact ce am notat și aici Cum
sunt unghiurile făcute de aceste
două perechi de drepte Păi unghiul
făcut de dreptele a și b este acesta
o să trec aici unghiul numărul
unu am spus că dintre un unghi
cu măsura mai mare și unul cu măsura
mai mică îl vom alege pe cel cu
măsura mai mică atunci când vorbim
de unghiul făcut de două drepte
iar unghiul făcut de dreptele c
și d este sista și trecem aici
2 cum sunt cele două unghiuri pe
ele sunt unghiuri cu laturile respectiv
paralele pentru că această latură
paralelă cu aceasta și aceasta
este paralelă cu aceasta prin urmare
ce va rezulta rezultă că unghiul
că măsura unghiului făcut de dreptele
a și b este egală cu măsura unghiului
făcut de dreptele c și d cele două
unghiuri 1 și 2 sunt unghiuri congruente
avem prin urmare teoremă dacă perechile
de drepte concurente a și b respectiv
c și d au proprietatea că a paralel
cu c și b paralel cu d x acea mutat
aici atunci măsura unghiului făcut
de dreptele a d este egală cu măsura
unghiului făcut de dreptele c d
important să reținem această teoremă
pentru vom aplica și în exerciții

.JPG)
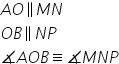
.JPG)