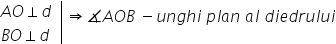Unghiul a două plane

în continuare să vedem Ce înțelegem

prin unghiul a două plane dar și

prin unghi diedru unghiul diedru

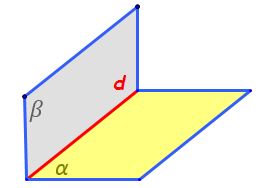
este figura geometrică în spațiu

formată de două semiplane care

au dreaptă în comun Iată avem aici

un semiplan aici un alt semiplan

și cele două semiplane au dreapta

d în comun această dreaptă pe care

le au în comun se numește muchia

diedrului iar cele două semiplane

se numesc fețele diedrului ce avem

aici este un unghi diedru cum determinăm

măsura unui asemenea unghi pe acest

unghi se măsoară prin unghiul său

plan Ce este acela unghi plan al

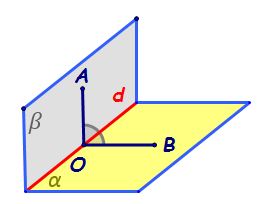
diedrului Iată unghiul plan al

unui diedru este format de două

semidrepte fiecare inclusă întru

un semiplan iar cele două semidrepte

sunt perpendiculare pe muchia diedrului

în același Deci ca să construim

un unghi plan al acestui unghi

drum trebuie să ne alegem un punct

pe dreapta pe muchia diedrului

și voi trece aici punctul o și

vom construit o semidreaptă inclusă

în acest semiplan iar această semidreaptă

trebuie să fie perpendiculară pe

dreapta d în acest punct o și a

doua semidreaptă este inclusă în

acest semiplan tot așa perpendiculară

pe dreapta d în punctul o unghiul

plan al diedrului este unghiul

format de aceste două semidrepte

deci vorbim de acest unghi măsura

unghiului diedru este dată de fapt

de măsura acestui unghi evident

că putem să construim o infinitate

de unghiuri plane pentru acest

diedru pentru băiat îl ne putem

alege un punct aici și tot așa

vândut c câte opt semidreaptă cum

am construit și aici însă unghiurile

care se vor obține Haideți Tutu

să construiesc acest unghi va fi

congruent cu acest unghi Deci prin

unghi plan al unui diedru înțelegem

un asemenea în construit exact

cum am făcut aici Ce înțelegem

prin unghiul a două plane și avem

aici două plane acest plan acesta

observăm că ele sunt plane secante

și aceasta este dreapta comună

Câte edre determină două plane

secante determină patru dietre

Iată avem aici un semiplan și cu

acest semiplan formează acest unghi

diedru apoi acest semiplan cu semiplanul

de jos formează al doilea unghi

diedru la fel acest semiplan cu

acesta formează al treilea unghi

diedru și acest semiplan cu cel

de sus formează al patrulea unghi

diedru Păi să construim câte un

unghi plan pentru fiecare din aceste

pietre și iată pupăm obține acest

desen și putem să Reprezentăm mai

clar unghiurile plane avem aici

un unghi plan Care este congruent

cu acesta cel care se află de des

8 și mai avem acest unghi care

e congruent cu cel de aici deci

practic Avem două măsuri de unghiuri

această măsură și aceasta cum procedam

când discutam despre unghiurile

formate de două drepte concurente

alegeam măsura alegeam unghiul

cu măsura cea mai mică absolut

la fel procedăm și aici Deci măsura

unghiului a două plane secante

este cea mai mică dintre măsurile

diedrelor formate de aceste planete

și pe desenul nostru se vede că

putem să alegem măsura acestui

unghi sau acest unghi ele sunt

lente Iată pentru că mă acestui

unghi are măsura mai mică decât

acesta Deci casă Determină măsura

unghiului făcut de două plane tot

așa ajungem la unghiul plan al

unui unghi diedru să facem acum

o aplicație Pe planul triunghiului

echilateral abc ab are 8 cm se

ridică perpendiculara de ei de

12 cm Deci triunghiul ABC este

triunghi echilateral toate lungimile

laturilor 8 cm și perpendiculara

Da are 12 cm se determină măsura

unghiului format de planele b a

d b a d de sunăm pe b cu d și c

a d c a d unii malcolm pe d cu

c și chiar putem să jurăm aceste

două plane ca să fie mai ușor de

identificat vorbim de acest clan

de acest plan se determină măsura

unghiului format de aceste două

plane pe mai întâi să vedem Care

este dreapta comună celor două

plane si foarte ușor de identificat

Iată planul b a d intersectează

planul c a d după ce dreaptă păi

se vede și din scriere și din desen

după dreapta a d bun acum trebuie

să construim un unghi plan al acestui

unghi format de cele două plane

cu alte cuvinte pe dreapta ad trebuie

ca în același punct să avem câte

două semidrepte perpendiculare

pe această dreaptă Evident semidreptele

să fie fiecare inclusă în unul

din cele două plane Cum facem asta

vă las puțin timp să vă gândiți

Păi nici mie am nevoie să facem

vreo construcție pentru că ele

sunt deja construite Iată mai știm

că d a este perpendiculară pe planul

a b c dar a b și a c sunt incluse

în planul abc asta înseamnă că

d a este perpendiculară și pe AB

De ce avem aici Unul de 90 de grade

și perpendiculară și pe ei ce voi

face aici și a mai mare ca să se

vadă și litera A bun Haideți să

notăm atunci Deci am obținut că

chiar să scriem complet de a este

perpendiculară pe planul abc ab

și ac sunt incluse în acest plan

abc Deci aici avem inclus rezultă

că dreapta d este perpendiculară

deci de a perpendiculară și pe

AB și da pandy cu Lara și pe ace

Sau dacă vreți ca să ne fie mai

clar putem să trecem invers că

a b perpendiculară pe da chiar

o să șterg Deci o să trec așa a

b perpendiculară pe d a și același

lucru îl voi face și aici deci

a c perpendiculară pe d a a c perpendiculară

pe d a ce am obținut aceasta este

muchia comună a celor două plane

a b perpendiculară pe a d a c perpendiculară

tot pe Ade înseamnă că măsura unghiului

P scrie aici măsura unghiului făcut

de planele V a d și c a d Cu cât

este egală Păi am construit de

fapt erau deja construit aceste

semidrepte egală cu măsura unghiului

format de ab și ac dreptele ab

și ac de putem numit te putem considera

a fi drepte fie semidrepte alte

cuvinte avem măsura unghiului b

a c Păi câte grade are acest unghi

are 60 de grade pentru că triunghiul

ABC este un triunghi echilateral

de c egal mai departe cu 60 de

grade și am determinat măsura unghiului

făcut de aceste două plane pentru

subpunctul b mic se determină măsura

unghiului format de planele abc

abc Deci acest plan de la bază

și b d c b d c bun.com Determină

măsura unghiului e făcut de aceste

două tot așa pe muchia comună Care

este b c ușor de văzut că ebc trebuie

să construim în același punct două

semidrepte perpendiculare pe BC

și Atenție nu o construim la întâmplare

ați văzut că uneori ele sunt deja

construite Cum a fost la subpunctul

a mic dar unde ori e nevoie chiar

să le construim velociped așa puțin

timp să vă gândiți Păi ce fel de

triunghi este triunghiul a b c

este un triunghi echilateral Ce

fel de triunghi este triunghiul

b d c Haideți să vedem avem aici

triunghiurile b a d și c a d știm

deja că aceste două triunghiuri

sunt triunghiuri dreptunghice avem

aici un unghi de 90 de grade la

fel și aici și ce au aceste triunghiuri

Păi au ei de latură comună și a

b este congruent cu a putem să

le tăiem aici cu o liniuță Deci

avem așa ei de latură comună voi

prescurta așa AB este egal cu ace

pentru că triunghiul ABC este triunghi

echilateral cum avem Două triunghiuri

dreptunghice Ce rezultă din cazul

catetă catetă înseamnă că triunghiurile

sunt congruente d și triunghiul

b a d este congruent cu triunghiul

c a d Ce rezultă prin urmare de

aici că b d este congruent cu d

c d c segmentul b d lungimea segmentului

BD este egală cu lungimea segmentului

DC Păi asta înseamnă că triunghiul

b d c este un triunghi isoscel

Deci notăm triunghiul b d c este

isoscel Păi deja lucrurile sunt

mult mai simple pentru că avem

aici un triunghi social iar triunghiul

a b c este un triunghi echilateral

atunci Cum construim cele două

drepte sau semidrepte perpendiculare

pe latura bc pe Alice în punctul

M mijlocul segmentului b c Deci

Fie m astfel încât BM este egal

cu m c și Avem așa triunghiul a

b c este un triunghi echilateral

d și triunghiul ABC este echilateral

o să prescurtez așa de m este egal

cu MC și Ce rezultă de aici că

a m este și înălțime în triunghiul

b a c Iată chiar o să trec aici

că avem un unghi drept Deci rezultă

că a m perpendiculară pe BC absolut

la fel ce vom obține Păi de vreme

ce avem un triunghi isoscel iar

m este mijlocul laturii bc înseamnă

că dm Iată este și ea perpendiculară

pe latura bc Deci venim și notăm

triunghiul b d c este isoscel b

m este egală cu m Ce înseamnă că

d m este perpendiculară pe b c

și deja lucrurile sunt foarte simple

pentru că avem Latura comună BC

și pe această latură comună în

punctul M avem de m și a m perpendicular

pe b c rezultă că Haideți să scriu

că cele două plane b d c și planul

a b c se intersectează în după

dreapta BC Deci rezultă din toate

aceste trei relații că măsura unghiului

format de planele vbc și ABC este

egală să vedem dacă avem spațiu

suficient cu măsura unghiului format

de dreptele d a m adică cu măsura

acestui unghi Iată care se vede

aici de m a și acum nu ne rămâne

decât să determinăm măsura acestui

unghi de m a Ce fel de triunghi

este triunghiul d a m d a este

perpendiculară pe planul a b c

a m este inclusă în acest plan

înseamnă că d a este Nicu Lara

pe a m nu voi mai facem aici semn

de perpendicularitate ca să nu

încărcăm prea mult desenul Deci

vom nota așa că da Deci d a perpendicular

pe a m înseamnă că avem triunghiul

d a m un triunghi dreptunghic cu

măsura unghiului d a m de 90 de

grade în acest triunghi dreptunghic

uitat mai vrem să determinăm măsura

acestui unghi Da de m a păi fiind

aici un triunghi dreptunghic în

acest unghi a atunci putem să aplicăm

de exemplu tangenta acestui unghi

pentru că noi cunoaștem lungimea

catetei Da este de 12 cm și putem

să determinăm și lungimea aceste

înălțimi A AM este înălțime în

triunghiul b a c Cu cât este egală

Păi știi că latura triunghiului

este de 8 cm Deci pentru că imi

perpendiculară pe BC multe si aici

relația 1 din relația 1 rezultă

că înălțimea în triunghi echilateral

este egală cu acest raport avem

lungimea laturii care La noi este

8 cm ori radical din 3 supra 2

deci vom avea așa 8 radical din

3 pe 2 adică 4 radical din 3 Dacă

nu Mai țineți minte A formula puteți

să deduceți lungimea lui lungimea

înălțimii a m din triunghiul a

m c avem un triunghi dreptunghic

aici avem 4 cm aici 8 cm aplicăm

Pitagora și determină Anca a m

are întradevăr 4 radical din 3

cm și acum aplicăm tangenta în

acest triunghi dam2 scrie aici

tangenta unghiului d m a d și tangenta

unghiului d m a este egală cu cateta

opusă unghiului Adică da supra

cateta alăturată adică a m înlocuim

și vom avea așa dar a 12 cm Deci

12 supra a m 4 radical din 3 și

vom obține de fapt radical din

3 Păi tangenta cărui unghi este

egală cu radical din 3 tangență

unui unghi cu măsura de 60 de grade

de C rezultă că măsura unghiului

d m are 60 de și sa încheiat pentru

că Iată măsura acestui unghi de

m a Care este de 60 de grade reprezintă

de fapt măsura unghiului făcut

de cele două plane