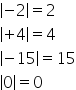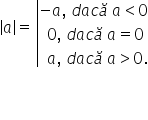Valoarea absolută a unui număr întreg
Tag-uri
Partajeaza in Google Classroom
Transcript
valoarea absolută sau modulul unui
număr întreg reprezintă distanța
de la origine până la poziția acestuia
pe axa numerelor am reprezentat
pe o axă câteva numere întregi
punctul o se numește originea axei
și acestui ia masa ciat numărul
întreg 0 să luăm câteva exemple
modulul numărului minus 2 va fi
2 pentru că distanța de la origine
până la numărul minus doi este
de două unități de măsură valoarea
absolută sau modulul se notează
cu două bare verticale și îmi scrie
că modulul numărului minus doi
sau valoarea absolută a numărului
minus doi este egal cu doi un alt
exemplu valoarea absolută a numărului
plus 4 va fi egală cu 4 pentru
că distanța de la origine până
la punctul D este de patru unități
de măsură valoarea absolută a numărului
minus 5 este 5:00 pentru că distanța
de la o la punctul a prim este
de 5 unități de măsură valoarea
absolută a numărului plus 3 este
3 și valoarea absolută a numărului
minus 3 va fi de asemenea 3 pentru
că distanța de la punctul o la
punctul c prim Este de trei unități
de măsură observăm că numerele
plus 3 și minus 3 deși sunt diferite
iar au aceeași valoare absolută
aceste numere plus trei și minus
trece nu lumii numere întregi opuse
Deci două numere întregi se numesc
opuse dacă ele au semne diferite
dar aceeași valoare absolută Manole
absolută a numărului zero va fi
0 să dorm și definiția numerelor
opuse opusul numărului întreg x
este numărul minus x astfel încât
x plus minus x să fie egal cu minus
x plus x și y egal cu zero Am văzut
că numerele minus trei și plus
trei sunt numere întregi opuse
asta înseamnă că minus trei este
opusul numărului plus 3 iar plus
trei este opusul numărului minus
3 înseamnă cu opusul numărului
minus 3 conform acestei definiții
respectiv notații va fi minus minus
3 care va fi egal cu plus 3 după
cum am văzut mai devreme putem
trage o concluzie atunci când avem
semnul minus de două ori el de
vapor duce la Semnul plus aceasta
va fi o regulă a semnelor pe care
vă rog să o rețineți pentru că
ne va fi utilă în rezolvarea exercițiilor
în care apar numere întregi să
vedem și alte exemple de numere
întregi opuse minus 7 și plus 730
și minus 30 minus 12 și plus 12
sau 243 și minus 243 în general
modulul unui număr întreg a este
minus A dacă A este negativ unde
prin minus a înțelegem opusul numărului
a adică modulul numărului minus
9 va fi opusul numărului minus
9 adică minus minus 9 Care este
plus 9 rețineți că valoarea absolută
a unui număr întreg este întotdeauna
un număr pozitiv valoarea absolută
a numărului a este 0 dacă a este
0 alte cuvinte modul de 0 este
egal cu 0 și valoarea absolută
a numărului a este A dacă A este
pozitiv adică valoarea absolută
a numărului 10 va fi 10 pentru
că 10 este un număr pozitiv în
continuare facem un exercițiu Calculați
la punctul a mic avem modul de
minus 25 plus modul de 4 ori modul
de minus unu valoarea absolută
a numărului minus 25 este 25 valoarea
absolută a numărului 4 este patru
și valoarea absolută a lui minus
1 este 1 obținem 25 plus 4 egal
29 iar la punctul b valoarea absolută
a numărului plus 7 minus valoarea
absolută a lui minus 3 plus valoarea
absolută a numărului 0 plus valoarea
absolută a numărului plus 6 împărțit
la valoarea absolută a numărului
2 moduri de plus 7 este 7 minus
valoarea absolută a lui minus 3
este 3 modul de zero este zero
modulul lui plus 6 este 6 și modulul
lui 2 este 2 egal șapte minus trei
este patru de zero este în se mai
scrie iar 6 împărțit la 2 este
3 4 plus 3 egal 7
Valoarea absolută a unui număr întreg. Numere întregi opuseAscunde teorie X
Navigare în lectii
Cumpara abonament
