Legile forţei de frecare. Rezolvarea problemei corpului pe un plan înclinat.
Tag-uri
Partajeaza in Google Classroom
Teorie: Forțe de frecare. Descarcă PDF
Forțe de frecare
Frecarea apare la suprafața de contact dintre două corpuri solide. Cauzele frecării sunt atât asperitățile celor două suprafețe ce intră în contact cât și atracția moleculară ce apare între cele două suprafețe. Asperitățile celor două suprafețe se întrepătrund și vot impiedica mișcarea celeor două suprafețe tangențial una față de alta. Macroscopic se va constata apariția unei forțe de rezistență ce se opune mișcării suprafețelor una față de alta.
Putem concluziona că forța de frecare este o forță de rezistență ce se opune mișcării relative a suprafețelor una față de alta.
Forța de frecare poate fi:
- forță de frecare statică;
- forță de frecare la alunecare;
- forță de frecare la rostogolire;
În continuare vom discuta de alunecarea unui corp ep o suprafață:
Dacă acționăm cu o forță de tracțiune asupra unui corp așezat pe un plan, corpul va rămâne nemișcat dacă forța de tracțiune este suficient de mică deoarece va fi egalată de o forță de frecare statică. Odată ce forța de tracțiune devine mai mare decât forța de frecare statică maximă, corpul începe să alunece accelerat pe plan. Forța de frecare la launecare este puțin mai mică decât forța de frecare statică maximă.
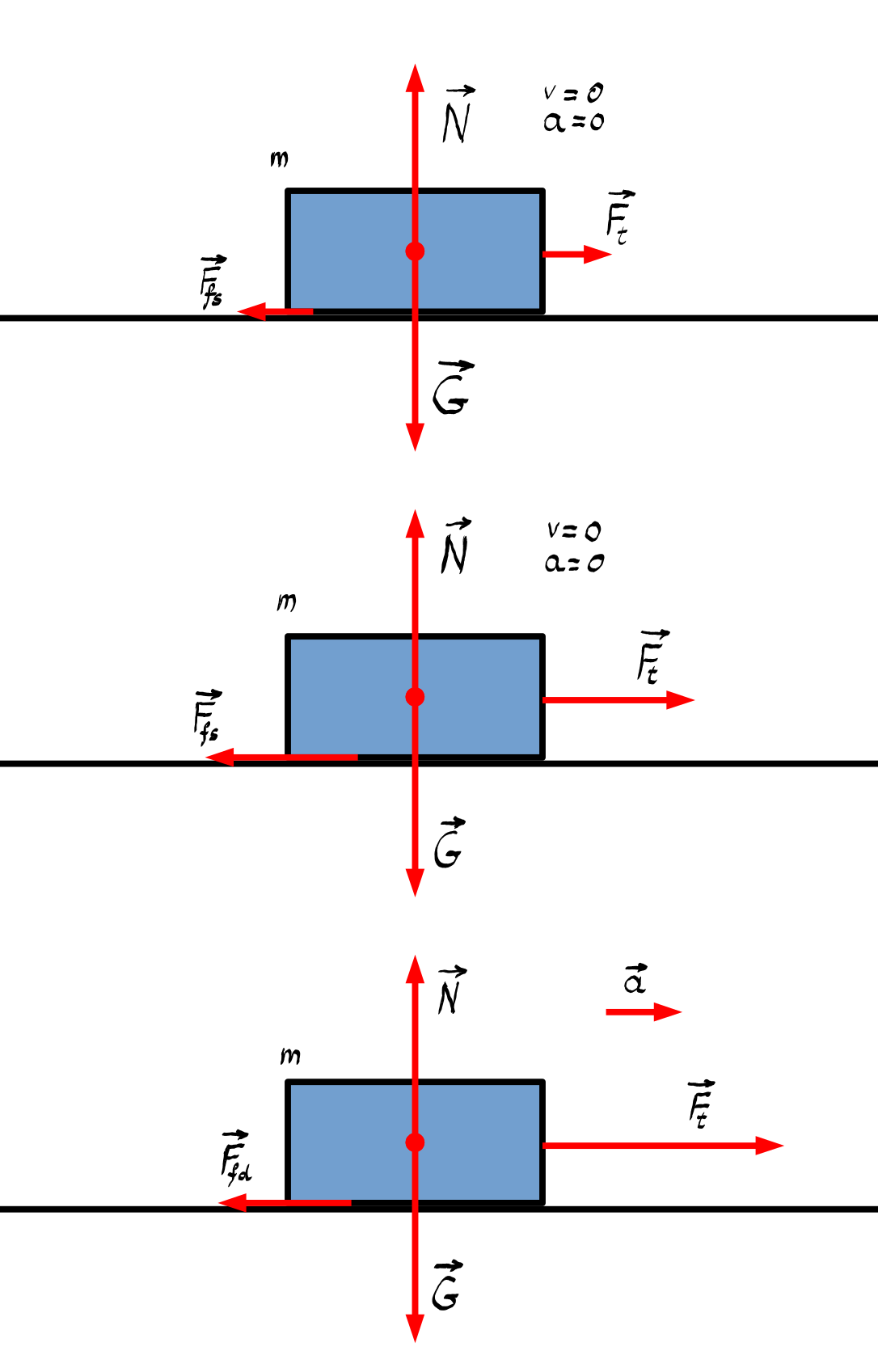
Experimental se demostrează că forța de frecare statică maximă este mai mare ddecât forța de frecare la alunecare, care la rîndul ei este mai mare3 decât forța de frecare la rostogolire.
Legile frecării
Legea I
Forța de frecare la alunecare este direct proporțională cu forța de apăsare exercitată de corp pe suprafața de alunecare care este egală în mărime cu forța de reacțiune normală la suprafața de contact dintre corpuri.
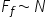
Legea aII-a
Forța de frecare la alunecare depinde de natura și gradul de prelucrare al suprafețelor aflate în contact. Dependența este careacterizată de o mărime adimensională numită coeficient de frecare al alunecare ce ia valor între 0 și 1 și se notează cu 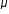 .
.
Legea a III-a
Forța de frecare al alunecare nu depinde de aria suprafeței de contact dintre corpuri.
În final putem scrie că forța de frecare este determinată de relația:
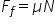
Planul înclinat. Unghiul de frecare.
Considerăm un corp de masă m ce alunecă uniform (cu viteză constantă) pe un plan înclinat sub unghiul 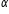 .
.
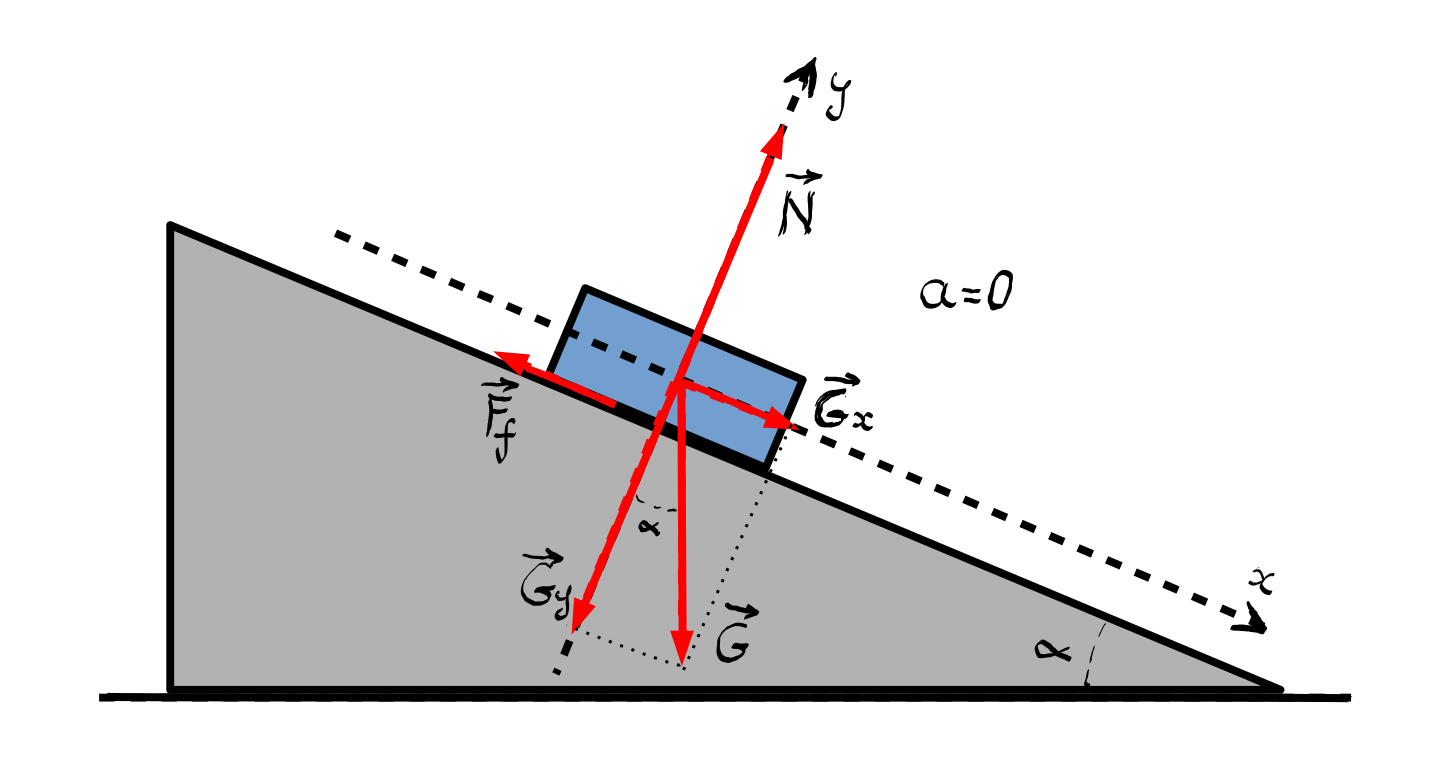
Asupra corpului vor acționa trei forțe, greutatea, reacțiunea normală la suprafață și forța de frecare. Deoarece corpul coboară uniform pe plan, accelerația sa este nulă.
Scriem:
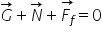
Proiectând pe cele două axe rezultă:
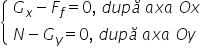
Proiecțiile greutății pe cele două axe sunt:
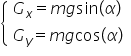
Înlocuim proiecțiile greutății, determinăm reacțiunea normlă la suprafață din ecuația după axa Oy și obținem forța de frecare:
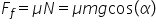
Înlocuim forța de frecare în relația după axa Ox și obținem:
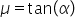
Deoarece coeficientul de frecare la alunecare depinde doar de unghiul planuluii înclinat, acest unghi se numește unghi de frecare.
Spunem că unghiul de frecare este unghiul unui plan înclinat la care un corp coboară pe plan cu viteză constantă.






