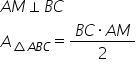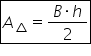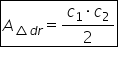Aria triunghiului

te duce mai întâi formula ariei

triunghiului dreptunghic prin aria

unui poligon în general înțelegem

porțiunea plană închisă determinată

de laturile sale pentru a te duce

formula ariei triunghiului dreptunghic

om desenat mai întâi Un dreptunghi

a b c d Maria amintesc că unitatea

de măsură pentru aria unei suprafețe

este metrul pătrat submultiplii

metrului pătrat sunt decimetrul

pătrat centimetru pătrat și milimetrul

Pătrat iar multiplii metrului pătrat

sunt decametrul pătrat hectometrul

pătrat și kilometrul pătrat nu

am construi o diagonală în acest

dreptunghi am dus diagonala bd

și putem observa că sau formată

Două triunghiuri dreptunghice acestea

sunt triunghiurile ABD și dbc putem

observa ca chestie triunghiuri

sunt congruente Deci ariile lor

vor fi egale Așadar voi scrie că

triunghiul ABD este congruent cu

triunghiul bdc ia din această relație

va rezulta că aria triunghiului

ABD va fi egală cu aria triunghiului

bdc voi nota laturile acestui dreptunghi

cu litere mici a și b știind că

între un dreptunghi Laturile opuse

sunt egale în clasa a cincea Ați

învățat formula ariei dreptunghiului

ca fiind lungimea ori lățimea Deci

aria lui ABCD este lungimea ori

lățimea lungimea sa notat cu litera

a mic iar lățimea cu b având în

vedere că cele două triunghiuri

care sau format au ariile egale

înseamnă că aria fiecărui triunghi

va fi jumătate din aria dreptunghiului

deci putem să scriem că a aria

triunghiului ABD este jumătate

din aria dreptunghiului Nici voi

scrie aria lui a b c d supra 2

Dar aria dreptunghiului este a

ori b supra 2 laturile a și b în

acest triunghi ABD sunt catete

Și atunci vom de duce că aria unui

triunghi dreptunghic este produsul

catetelor sale supra 2 deci putem

să scriem egal în continuare cateta

unu ori cateta doi supra 2 Așadar

rețineți că a aria unui triunghi

dreptunghic în cazul acesta aria

triunghiului ABD este produsul

catetelor supra 2 aceasta va fi

formula pe care omul folosi în

continuare în rezolvarea problemelor

să te ducem acum aria triunghiului

ascuțitunghic construim un triunghi

ascuțit unghic abc mai face o construcție

ajutătoare pentru a afla aria acestui

triunghi mai exact voi construi

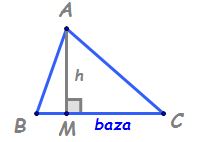
înălțimea din a aceasta este a

m observăm că sau format Două triunghiuri

dreptunghice abm și a m c am duce

a m perpendiculară pe BC aria triunghiului

ABC va fi formată din aria triunghiului

abm plus aria triunghiului AMC

triunghiul abm este dreptunghic

în m și aria acestui triunghi va

fi produsul catetelor sale supra

2 mai scrie că aria triunghiului

abm va fi egală cu a m ori bem

supra 2 pentru că a m și b m sunt

catetele acestui triunghi dreptunghic

apoi aria triunghiului a m c este

de asemenea produsul catetelor

supra 2 catetele acestui triunghi

sunt a m și m c și atunci din aceste

trei relații putem scrie că aria

triunghiului ABC este suma acestor

arii în loc de aria triunghiului

abm voi scrie a m ori b m supra

2 plus în loc de aria triunghiului

AMC voi scrie a n ori m c supra

2 pentru a aduna două fracții cu

același numitor adunăm numărătorii

iar numitorul comun se copiază

voi scrie a m ori bem plus a m

ori Mc totul supra 2 la numărător

putem să dăm factor comun pe a

m scrie a m pe lângă a b m plus

m c totul supra 2 egal mai departe

cu a m ori bem plus Mc dacă ne

uităm pe figură va fi egal cu bc

supra 2 a m este înălțimea în acest

triunghi iar BC este lot la corespunzătoare

înălțimii pe care o Vom numi baza

triunghiului așa Dar în general

formula de calcul pentru aria unui

triunghi ascuțitunghic este semi

produsul dintre baza triunghiului

și înălțimea corespunzătoare a

scrie Acest lucru b ori supra 2

unde b este baza iar h este înălțimea

triunghiului rețineți această formulă

ia se va aplica în rezolvarea problemelor

acum trebuie să deducem formula

ariei unui triunghi în cazul în

care triunghiul este obtuzunghic

am construit un triunghi abc obtuzunghic

va face și în acest caz o construcție

ajutătoare îl duce înălțimea din

a pe latura bc pentru a putea construi

perpendiculara din A pe BC va trebui

mai întâi să prelungim latură b

c pentru că piciorul perpendicularei

o să fie În exteriorul triunghiului

am dus a m perpendiculară pe BC

și ne propunem să găsim o formulă

de calcul pentru aria triunghiului

ABC conform figurii pe care am

construit o putem observa că aria

triunghiului ABC este diferența

dintre aria triunghiului a m c

și aria triunghiului a m b scrie

Așadar egal cu aria triunghiului

AMC minus aria triunghiului a m

b aria triunghiului AMC este produsul

catetelor supra 2 pentru ca acest

triunghi este un triunghi dreptunghic

a tele sale sunt a și m c iar triunghiul

amb fiind și acesta un triunghi

dreptunghic aria sa va fie produsul

catetelor supra 2 catetele sunt

a m și m b scădem numărătorii a

n o m c minus a m ori MD totul

supra 2 la numărător putem să dăm

factor comun pe a m voi scrie a

m pe lângă m c minus m b supra

2 egal în continuare dacă ne uităm

pe figură observăm că m c minus

m b este chiar segmentul b c Așadar

putem deduce că aria triunghiului

a b c este semi produsul dintre

bază și înălțimea corespunzătoare

a scrie Acest lucru b ori H supra

2 putem observa că am obținut aceeași

formulă ca și în cazul triunghiului

ascuțitunghic în general formula

de calcul pentru a oricărui triunghi

este baza ori înălțimea supra 2

Chiar și în cazul triunghiului

dreptunghic se poate aplica această

formulă pentru că am văzut că înălțimea

și bază coincid chiar cu cele două

capete ale sale în continuare o

să facem câteva probleme am scris

cele două formule pentru aria triunghiului

dreptunghic cateta ori catetă supra

2 iar în cazul general aria unui

triunghi este baza ori înălțimea

supra 2 ne propunem în continuare

să rezolvăm o problemă Calculați

aria unui triunghi dreptunghic

cu catetele de 6 cm și 8 cm triunghiul

ABC fiind dreptunghic catetele

acestuia sunt a b și b c AB este

6 cm iar BC este 8 cm Aria acestui

triunghi va fi egală cu a b ori

b c supra 2 egal în continuare

cu 6 ori 8 supra 2 egal cu 48 supra

2 După efectuarea împărțirii obținem

24 cm pătrați următoarea problemă

intru în triunghi o înălțime este

de 5 cm și aria triunghiului este

de 30 cm pătrați Aflați lungimea

laturii corespunzătoare înălțimii

date să scriem formula ariei unui

triunghi aceasta este baza ori

înălțimea supra 2 și știm din datele

problemei că aria este egală cu

30 de cm pătrați nu cunoaștem bază

însă știind că înălțimea este de

5 cm Deci beau 5 supra 2 va fi

egal cu 30 m o relație din care

trebuie să aflăm necunoscute b

fiind o proporție aplică în proprietatea

fundamentală a proporțiilor produsul

mezilor egal cu produsul extremilor

Deci obținem că b ori 5 va fi egal

cu 2 ori 30 b ori cinci este egal

cu 60 ca să aflăm necunoscute b

împărțim aceasta egalitate cu 5

și obținem b egal cu 60 împărțit

la 5 Deva fie egal cu 12 cm Deci

latura corespunzătoare înălțimii

va fi 12 cm