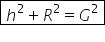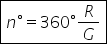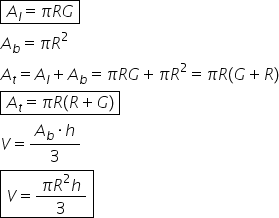Conul circular drept (descriere, desfășurare, formule)

să discutăm acum despre conul circular

drept Care sunt elementele lui

bază este un cerc Iată iar suprafața

laterală se desfășoară în plan

după un sector de cerc ce am reprezentat

aici cu mov este desfășurarea suprafeței

laterale iar cercul de la baza

Iată se regăsește înfășurăm de

acest sector de cerc astfel încât

această parte să se suprapună perfect

peste aceasta vom obține un con

circular drept să trecem și elementele

voi nota aici cu o centrul cercului

de la baza Deci trebuie să trecem

și aici tot o vorbind de același

cerc și să notăm cu R mic raza

cercului Deci trecem irmak generatoarea

conului este aceasta și atenție

generatoarea conului reprezintă

de fapt raza acestui sector de

ce înălțimea unui con adică acest

segment care este perpendicular

pe baza trece prin centrul cercului

de la bază și putem să nu uităm

aici cu v v o este înălțimea o

să trec și aici și raza o putem

nota de exemplu și o să găsim acum

formulele pentru aria laterală

aria totală și volumul în să facem

mai întâi o observație foarte importantă

și anume Deci trecem aici atenție

Ce observăm înălțimea este diferită

de generatoare Deci nu se întâmplă

cu mâța în camera la cilindru circular

drept în care generatoarea era

congruentă cu înălțimea cilindrului

aici înălțimea este diferită de

generatoarea conului cum determinăm

acum o formula pentru aria laterală

aria laterală reprezintă de fapt

Aria suprafeței laterale adică

aria acestui sector de cerc atunci

să notăm egal cu aria sectorului

de cerc Păi Cu cât este egală aria

unui sector de cerc trecem aici

aria unui sector de cerc în acest

caz e este egală cu nea mintim

formula și avem fie înmulțit cu

rază la a doua aici la asta este

reprezentată de generatoare de

ce avem si pătrat pentru că vorbim

de raza acestui sector de cerc

supra 360 de grade înmulțit cu

n grade unde n grade reprezintă

măsura unghiului sectorului de

cerc adică aici avem n mic grade

aria laterală poate fi exprimată

sub această formă pur Gela a doua

supra 360 înmulțit cu n grade însă

dacă nu știm măsura acestui unghi

atunci lucrurile sunt mai complicate

puțin De aceea să facem în așa

fel încât să exprimăm aria laterală

fără să ne mai apară aici măsura

acestui unghi Cum să facem acest

lucru pe ce mai cunoaștem Iată

acest cerc se obține din înfășurarea

acestui sector de cerc astfel încât

acest punct să se suprapună perfect

peste acesta și astfel se obține

la bază cercul respectiv pe Ce

înseamnă asta înseamnă că lungimea

acestui cerc este egală cu lungimea

arcului de aici arcului sectorului

de cerc deci putem să trecem că

lungimea cercului mă refer la lungimea

acestui cerc lungimea cercului

de la baza este egală cu lungimea

arcului sectorului de cerc Păi

Cu cât este egala Lungimea unui

cerc cu rază r mic știm deja Avem

doi fii orar mic egal cu lungimea

arcului sectorului de cerc mă refer

la acest ar este egală cu trecem

aici înmulțit cu raza Care este

G supra 180 de grade înmulțit cu

n grade măsura acestui unghi Păi

ia că de aici putem să exprimăm

en grade adică măsura acestui unghi

și apoi ce vom obține vom înlocui

aici în această relație deci de

aici rezultă că avem in grade este

egal cu 2 pe orar 180 de grade

2 ori el ori 180 de grade supra

pai orice sigur putem să simplificăm

aici pe și prin piși ne rămâne

aici unul și unul Deci vom obține

2 r ori 180 de grade supra g și

acum nu facem altceva decât să

înlocuim ce am obținut aici pentru

in grade adică această expresie

omul locuit aici și vom avea că

aria sectorului de cerc Iată voi

copiat din nou egal cu trecem aici

Deci rezultă fie înmulțit cu ge

la a doua supra 360 de grade înmulțiri

cu n grade care ia t n grade egal

cu cea notat aici Deci o să copiem

bun și acum vedem ce avem de calculat

360 de grade cu 180 de grade simplificăm

ne rămâne aici și unu și aici doi

doi cu doi la fel simplificăm Ne

rămâne 1 și 1 g pătrat și g simplificăm

prin și ne rămâne aici Unul aici

ne rămâne ge la puterea întâia

o să tai doar exponentul și am

obținut orice orar de sigle mai

departe cu păr mic orice să notăm

prin urmare că aria de Ce rezultă

de aici că aria laterală se poate

scrie și sub această formă aria

sectorului de cerc adică p r g

p r ori prin urmare acestea sunt

cele două metode prin care putem

să exprimăm aria laterală acum

ștergem aici ca să exprimăm și

formula să scriem și formula pentru

aria totală sigur II ușor de bănuit

că aria totală cu aria laterală

plus aria bazei adică aria laterală

e cea avem aici orar orice plus

aria bazei pe baza este un cerc

de rază r mic adică permit la pătrat

putem acum să dăm factor comun

pe picior aer Și atunci vom avea

că aria totală este egală cu fier

pe lângă G adunat cu el Până mai

rămas acum decât să exprimăm volumul

formula pentru volum este următoarea

avem aria bazei ori înălțimea supra

3 putem să zicem așa aria bazei

ori înălțimea supra 3 Deci egal

mai departe cu aria bazei înseamnă

pir mic la pătrat ori înălțimea

supra 3 mai facem acum o singură

observa și anume Ce legătură este

între generatoarea conului înălțimea

conului și raza cercului de la

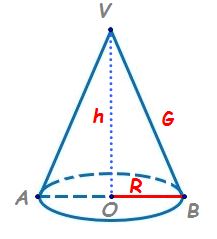
baza Păi foarte simplu de intuit

avem aici triunghiul v o a Care

este un triunghi dreptunghic în

o Deci avem măsura unghiului înainte

o să trec și această relație aici

Deci avem măsura unghiului v o

a este egală cu 90 de grade atunci

rezultă din teorema lui Pitagora

si vom obține că vei la pătrat

adică gen la a doua lungimea generatoarei

la pătrat egal cu h la a doua plus

R mic la a doua și iată că am găsit

Ce relație există între generatoarea

conului înălțimea conului și raza

cercului de la bază să încadrăm

relația și am obținut a astfel

formula pentru aria laterală a

unui con circular drept aria totală

și volumul