Divizor. Multiplu. Noțiuni introductive
Tag-uri
Partajeaza in Google Classroom

Transcript
Haide să vedem acum Ce este acela
un divizor și Ce este un multiplu
și vom începe cu acest exemplu
Vrem să vedem dacă 2 este un divizor
sau dacă 2 îl divide pe 6 pe trebuie
să vedem de fapt dacă 2 îl împarte
pe 6 în părți egale cu el însuși
adică în părți egale cu doi sigur
șase poate fi scris doi plus doi
plus doi din această cauză putem
spune că 2 îl divide pe 6 pentru
că doina împărțit pe 6 în trei
părți egale cu fiecare parte fiind
egală cu doi de ce are loc această
scriere Păi are loc această scriere
pentru că 6 împărțit la A2 Este
cam spus o împărțire exactă alt
exemplu patru putem spune că îl
divide pe 6 adică pe 6 L Scrie
sub această formă 4 plus 4 plus
și așa mai departe a dat deja nu
e bine pentru că 4 cu 4 ne dă 8
Dacă mai adunăm ceva o să obținem
un număr mai mare Deci venim și
notăm 4 nu îl divide Deci nu divide
pe 6 De ce nu se întâmplă asta
pentru că patru nu se cuprinde
6 de un număr exact de ori încă
un exemplu 3 îl divide o are pe
6 pe ea să vedem pe 6 îl putem
scrie în funcție de trei sigur
avem aici trei plus trei deci trei
îl divide pe 6 repet de ce se întâmplă
acest lucru De ce are loc această
scriere pentru că șase se împarte
exact la trei de ceai de să notăm
6 împărțit la 3 este o împărțire
prescurtam așa exakta cu alte cu
6 împărțit la 3 ne dă de fapt 2
rest 0 restul 0 ne arată și o împărțire
exactă iar 3 intră în 6 de două
ori iar 3 plus 3 cu alte cuvinte
Ca să verificăm Dacă un număr divide
alt număr trebuie să fie vedem
dacă cum e aici Dacă doi Se cuprinde
în 6 de un număr egal de ori și
acum cum notăm Păi 2 în divide
pe 6 bancnota astfel Deci avem
2 și 6 ca Să arătăm că 2 îl divide
pe 6 vom trece această bară verticală
citim Cum înscris aici 2 divide
pe 6 4 divide pe 6 nu îl divide
pe 6 atunci cum credeți că scrie
această bară O fată ia cu o linie
citim 4 nu îl divide pe 6 și aici
trei îl divide pe 6 Altex ample
Haideți să notăm Să considerăm
acum numărul 4 să vedem dacă 4
îl divide pe 12 și trecem aici
semnul întrebării să vedem dacă
între adevăr se întâmplă acest
lucru Cum verificăm Păi vedem dacă
4 Se cuprinde în 12 de un număr
extract de ori cu alte cuvinte
12 împărțit la 4 este o împărțire
cu restul 0 ne dă 3 rest 0 având
o împărțire exactă înseamnă că
4 îl divide întradevăr pe 12 pentru
că Iată pe patul putem pe 12 îl
putem Scrie patru plus patru plus
patru patru intră în 12 de trei
ori să vedem dacă 5 îl divide pe
20 Cum verificăm vedem dacă deci
cu semnul întrebării se vedem dacă
20 se împarte exact la 5 Adică
dacă acest număr Se cuprinde în
20 de un număr extract de ori pâine
de 4 rest 0 din nou avem restul
0 împărțit exact înseamnă că 5
îl divide întradevăr pe 20 dar
6 să vedem acum Dacă 6 îl divide
pe 20 pe Cum verificăm vedem dacă
20 se împarte exact la 6 obținem
3 trei ori 6 ne dă 18 și avem aici
și o 20 minus 18 doi Deci avem
trei rest 2 cam restul este diferit
de 0 înseamnă că nu avem Deci nu
este o împărțire exactă din această
cauză pentru că nu avem împărțire
exactă înseamnă că 6 nu îl divide
pe 20 și simbolul de divizibilitate
la am tăiat cu această linie roșie
pentru că ea 6 nu se cuprinde în
20 de un număr extract de ori si
avem 6 adunat cu 6 plus 6 aici
obținem 18 plus doi ne mai trebuie
doi ca să ajungem la 20 dec clar
că șase Nu Se cuprinde în 20 de
un număr exact de ori alt exemplu
8 îl divide pe 24 pe Cum verificăm
avem de fapt două variante de verificare
ele sunt modalități echivalente
Prima variantă să nu te mai ci
1 vedem dacă 24 se împarte exact
la 8 Deci 24 împărțit ID este 509
de întrebare că verificăm împărțit
la 8 ne dă 3 rest 0 Păi restul
este 0 o împărțire exactă asta
înseamnă că întradevăr 8 îl divide
pe 24 sau o altă variantă de rezolvare
care Deci sau care este de fapt
echivalentă a doua variantă este
următoarea vedem dacă există vreun
număr natural care înmulțit cu
8 Haideți să păstrez culorile dacă
înmulțit cu 8 ne dă 24 pe există
un asemenea număr sigur Vorbim
de numărul 3 Deci avem aici 3 înmulțit
cu 8 ne dă 24 fie faceți așa Verificați
dacă împărțirea exactă fi vă întrebați
dacă există vreun număr care înmulțit
cu 8 ne dă 24 un număr natural
de ce vom prezenta și această variantă
pentru că în general în manuale
sau culegeri definiția este aceasta
spunem că a îl divide pe b dacă
Haideți scriu cu altă culoare dacă
există un număr natural un număr
natural Haide sa spunem si astfel
încât are loc această relație ce
înmulțit cu ei să fie egal cu b
poate cuvinte Exact ce am făcut
aici Iată trei există acel număr
natural care este 3 care înmulțit
cu 8 nea dat 24 Deci fie faceți
așa fie Vă gândiți la această variantă
care reprezintă de fapt definiția
mie personal în pace să folosesc
această variantă în care folosim
împărțirea și acum să mai dăm încă
un exemplu 3pl de divide oare pe
21 Păi trebuie să vedem dacă întradevăr
21 împărțit la 3 împărțire exactă
și obținem 7 rest 0 având o împărțire
exactă înseamnă Că întradevăr 3
divide pe 21 bun pentru că se întâmplă
acest lucru spunem că trei se numește
divizor în timp ce 21 se numește
multiplu Deci pentru că 3 divide
pe 21 el se numește divizor și
dec 21 se numește multiplu pentru
că de fapt 21 se obține prin multiplicarea
lui 3 Iată din teoremă împărțirii
cu rest această relație o putem
Rescrie ca fiind 21 egal cu 3 înmulțit
cu 7 Păi 21 se obține prin multiplicarea
lui 3 de șapte ori Deci notăm că
21 este un multiplu al lui 3 iar
3 este un divizor al lui 21 se
gândi și așa 7 îl divide pe 21
sigur pentru că 21 împărțit la
șapte ne dă 3 rest 0 sau altfel
spus 2121 se scrie ca fiind 7 ori
3 Deci 21 este un titlu și D7 Lari
este un multiplu și de 3 să notăm
aici 7 este un divizor al lui 21
din timp ce 21 este un multiplu
al numărului 721 este multiplu
și de trei și de 7-a Cum facem
câteva observații legate de această
notație am scris până acum că 3
divide pe 21 sau un alt exemplu
am avut așa 7 divide pe 21 sau
putem să notăm și că 21 îl divide
pe 21 e adevărat relația sigur
pentru că 21 împărțit la 21 ne
dă 1 rest 0 Deci avem o împărțire
exactă bun Ce observăm că peste
tot scris mai întâi numărul mic
urmat de numărul mare sau am avut
aici numere egale însă Putem să
scriem și Invers adică am putea
să scriem aici că 21 îl divide
pe 7 Ne întrebăm 7 împărțit la
21 împărțire exactă nu deci această
scriere nu are 700 nu are loc bun
Dacă nu are dacă vrem să scriem
totuși mai întâi numărul mare urmat
de numărul mic atunci vom schimba
notația astfel putem să notăm că
21 Haideți uităm la prim exemplu
21 și trecem aici pe 3 atunci între
ele vom trece trei puncte citim
21 este divizibil cu 3 Deci 21
divizibil cu 3 aici Cum citim spunem
că trei divide pe 21 dec acest
semn a prezentat de bară citim
divide pe iar aici când avem trei
puncte trece mai întâi numărul
mare urmat de cel mic și citind
divizibil cu la fel Putem să scriem
și aici 21 este divizibil cu 7
sau 21 este divizibil cu 21 prin
urmare reținem că cele două relații
acestea sunt de fapt relații echivalente
și atunci când avem ambele numere
diferite de 0 când cel puțin unul
din numere 0 atunci nu mai aplicăm
această regulă cu mai mic sau mai
mare O să vedeți Deci când am prea
numere sunt diferite de 0 atunci
dacă vrem să scrie mai întâi numărul
mic urmat de cel Mare folosim scrierea
cu bară dacă vrem însă să scrie
mai întâi numărul mare urmat de
cel mai vom folosi această scriere
cu trei puncte Cum verificăm dacă
21 este divizibil cu 3 pe la fel
ca aici vedem dacă 21 se împarte
exact la 3 și cum avem o împărțire
cu rest 0 clar putem spune că 21
este divizibil cu 3 ce se întâmplă
însă când cel puțin unul din numere
este de exemplu putem să spunem
că zero îl divide pardon că îți
dă îl divide pe 12 și să trecem
aici cu semnul întrebării Cum verificăm
dacă o asemenea relație are loc
Păi vedem dacă 12 împărțit la 0
eu împărțire exactă banda putem
noi Să împărțim un număr la 01
această împărțire Nu are sens din
această cauză spunem că 0 nu îl
divide de fapt pe 12 absolut la
fel 10 putem să nu uităm că 12
nu e divizibil cu deci nu e divizibil
cu 0 Din ce cauză pentru că împărțirea
12 împărțit la 0 iată nu are sens
bun dar ce împărțire are sens o
putem să împărțim pe 0 la 12 și
ne dă 0 rest 0 Iată împărțire exactă
bun pe asta înseamnă că de fapt
Putem să scriem că nu se divide
pe 12 și invers 12 îl divide pe
0 sau altfel spus relației echivalentă
dacă folosim scrierea cu trei puncte
atunci mai întâi vom trece pe 0
divizibil cu 12 pentru că are loc
împărțirea a 0 împărțit la 12 iar
este o împărțire cu rest 0 iau
împărțire exactă de fapt iată că
aici Deși folosim scrierea cu bară
nu mai ia pe aici nu mai ținem
cont de regula pe care a spus înainte
sau de mai întâi numărul mic urmat
de cel Mare Deci când ne apare
aici și zero lucrurile sunt puțin
diferite și putem să reținem acest
fapt și anume că Haideți să scriem
cu altul că dacă 0 nu divide de
fapt niciun număr natural de teze
ronul divide pe a Oricare ar fi
a număr natural de 50 nu divide
pe 0 0 1 divide pe 1 0 1 1 divide
pe 2 și așa mai departe sau nu
are loc nici relație echivalentă
0 nu este divizibil cu 0 1 1 este
divizibil cu 0 2 nu este divizibil
cu 0 și așa mai departe de ceai
de să reținem și această relație
care de fapt să scrie puțin diferit
Deci nu scrie încă 0 îl divide
pe 12 și 12 divide pe 0 sau 0 este
divizibil cu 12

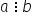 , citim 'a este divizibil cu b'
, citim 'a este divizibil cu b'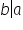 , citim 'b divide pe a'
, citim 'b divide pe a'