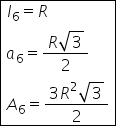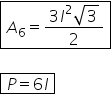Latura, apotema și aria hexagonului (teorie)

în această lecție o să calculăm

latura apotema și aria hexagonului

regulat înscris în cerc în funcție

de raza cercului a b c d e f este

un hexagon regulat Acesta are șase

laturi și șase unghiuri congruente

segmentele o b și o c sunt raze

ale cercului circumscris iar om

este apotema pornind de la aceste

formule pe care le am găsit între

o lecția anterioară când am discutat

despre Poligonul regulat cu n laturi

în cazul hexagonului n este 6 și

atunci latura hexagonului L6 va

fi egală cu 2 r ori sinus de 180

de grade supra 6 egal cu 2 r ori

sinus de 30 de grade egal cu 2

ori 1 supra 2 se simplifică 2 și

obținem R prin urmare latura hexagonului

este egală cu raza cercului Apotema

hexagonului A6 este egală cu r

cosinus de 180 de grade supra 6

egal cu r ori cosinus de 30 de

grade egal cu radical din 3 supra

2 și egal cu rază radical din 3

pe 2 aria hexagonului este egală

cu 6 iar la a doua sinus de 180

de grade supra 6 ori cosinus de

180 de grade supra 6 egal cu 6

aer la a doua ori sinus de 30 de

grade este 1 supra 2 iar cosinus

de 30 de grade este radical din

3 pe 2 se simplifică 6 cu 2 și

obținem trei herla doua radical

din 3 supra 2 aceasta va fi formula

ariei în funcție de raza cercului

circumscris dacă dorim să calculăm

aria în funcție de latura hexagonului

obține formulă a 3 n la a doua

radical din 3 supra 2 pentru că

raza este egală cu latura perimetrul

hexagonului este 6 ori n și egal

cu șase ori raza cercului circumscris

în cazul în care nu dețineți aceste

formule de la care am pornit și

șansele să se întâmple asta sunt

destul de mari propun și eu o altă

metodă de a calcula apotema latură

și aria hexagonului în funcție

de raza cercului circumscris observăm

că acest cerc este împărțit în

șase arce congruente măsura unui

arc este egală cu 360 de grade

împărțit la 6 pentru că un cerc

întreg are 360 de grade și atunci

măsura arcului bc este egală cu

360 de grade împărțit la 6 egal

cu 60 de grade Să calculăm măsura

unghiului la centru b o c măsura

acestui unghi este egală cu măsura

arcului cuprins între laturile

sale adică Măsura arcului bc și

egal cu 60 de grade însă triunghiul

b o c este un triunghi isoscel

pentru că are două laturi congruente

iar un triunghi isoscel cu un unghi

având măsura egală cu 60 de grade

este 1 km echilateral prin urmare

triunghiul b o c este echilateral

Deci latura bc va fi egală cu raza

cercului circumscris adică Latura

este egală cu raza am arătat printru

alta modalitate că latura hexagonului

este egală cu raza cercului circumscris

apotema este om om este înălțime

în triunghiul echilateral b o c

în lecția în care am de terminat

formulele de calcul pentru latura

și apotema triunghiului echilateral

am găsit și o formulă de calcul

pentru înălțimea triunghiului în

funcție de latura acestuia astfel

înălțimea în triunghi echilateral

este latura radical din 3 supra

2 această formulă se poate obține

foarte simplu Aplicând teorema

lui Pitagora În triunghiul o m

c latura infinit egală cu raza

obținem astfel că apotema Poligonului

este raza radical din 3 supra 2

am găsit și formula de calcul pentru

apotema hexagonului în funcție

de raza cercului circumscris mai

trebuie să calculăm aria acestuia

observăm că acesta este împărțit

în 6 triunghiuri echilaterale congruente

și atunci aria hexagonului va fi

egală cu șase ori aria triunghiului

Boc egal cu șase ori aria triunghiului

echilateral este latura la a doua

radical din 3 supra 4 se simplifică

6 și 4 prin 2 ne rămâne 3 și 2

egal cu 3 l la a doua radical din

3 supra 2 dacă dorim să exprimăm

aria funcție de raza cercului atunci

aria hexagonului va fi egală cu

3 la a doua radical din 3 supra

2 am găsit și formula de calcul

pentru aria hexagonului funcție

de raza cercului