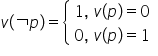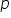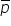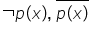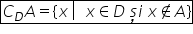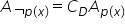Negația propozițiilor și a predicatelor. Complementara unei mulțimi

Maria amintesc că logica studiază

propozițiile din punct de vedere

al valorii lor de adevăr pornind

de la o propoziție dată sau de

la un predicat putem obține alte

propoziții respectiv predicate

cu ajutorul operațiilor logice

aceste operații sunt negația conjuncția

disjuncția implicația și echivalența

în această lecție o să discutăm

despre prima operație negația o

să vedem cum putem să obținem negația

unei propoziții și a unui predicat

și apoi o să discutăm despre complementară

unei mulțimi Fiind dată o propoziție

pe negația aceste propoziții se

notează astfel se citește non pe

și ea este adevărată atunci când

pe este falsă și falsă dacă este

adevărată prin urmare valoarea

de adevăr a propoziției non p este

egală cu 1 dacă valoarea de adevăr

a propoziției pe este zero și zero

dacă valoarea adevăr a propoziției

pe este 1 acesta este și tabelul

valorilor de adevăr prin urmare

dacă pe este falsă Nan pe este

adevărată și invers dacă p este

adevărată negația acestuia este

o propoziție falsă să facem câteva

exemple în prima coloană am scris

câteva propoziții iar în această

coloană a scris negațiile acestora

prima propoziție 30 este divizibil

cu doi este o propoziție adevărată

Deci valoarea de adevăr a acestuia

este 1 negația propoziției este

următoarea 30 nu este divizibil

cu 2 iar Aceasta este o propoziție

falsă prin urmare valoarea de adevăr

a propoziției non p este 0 diagonalele

în romb sunt perpendiculare este

o propoziție adevărată negația

acesteia diagonalele între un romb

nu sunt perpendiculare este o propoziție

falsă unu plus trei este egal cu

4 este o propoziție adevărată 1

plus 3 este diferit de 4 este o

propoziție falsă radical din 2

este număr întreg Aceasta este

o propozitie falsă dar de cal din

2 nu este număr întreg este o propoziție

adevărată normale negația unei

propoziții se obține Transformând

o propoziție afirmativă o propoziție

negativă sau folosind negațiile

unor simboluri matematice de exemplu

simbolul egal a fost înlocuit cu

simbolul diferit să vedem în continuare

Cum putem obține negația unui predicat

fiind dat un predicat pdx negații

acestui predicat se notează în

felul următor și astfel se obține

un predicat Care este adevărat

pentru acele valori ale lui x pentru

care p de x este fals și Este fals

pentru acele valori ale lui x pentru

care p de x este adevărat în prima

coloană avem niște predicate iar

în a doua coloană avem negațiile

acestora de exemplu Primul predicat

x plus unu mai mic decât 0 unde

x este număr real iar negația acestuia

este predicatul x plus 1 mai mare

sau egal decât 0 x număr real apoi

al doilea predicat 2 x este egal

cu 0 negația acestuia 2 x este

diferit de 0 5 la x este egal cu

25 negații acestuia 5 la x este

diferit de 25 să discutăm în continuare

despre complementară unei mulțimi

și o să vedem că există o strânsă

legătură între negația unui predicat

și complementare unei mulțimi avem

o mulțime de și ei o submulțime

a acesteia atunci mulțimea elementelor

care aparțin mulțimii de dar nu

aparțin mulțimii a formează complementara

mulțimii A în raport cu d și se

notează astfel complementara mulțimii

A în raport cu mulțimea b este

formată din acele elemente x cu

proprietatea că x aparține lui

d dar x nu aparține lui a pe această

diagramă este vorba de această

porțiune hașurată Deci în această

zonă avem complementarea mulțimii

A în raport cu mulțimea D și acum

să vedem ce legătură există între

negația unui predicat și complementare

unei mulțimi Maria amintesc că

mulțimea de adevăr a unui predicat

predicat formează din acele elemente

x din domeniul de valori ale predicatului

cu proprietatea că propoziția pe

x este adevărată atunci mulțimea

de adevăr a negației predicatului

este complementară mulțimii de

adevăr a predicatului p de x în

raport cu mulțimea D De exemplu

dacă avem acest predicat pe de

x x mai mic decât 5 unde x este

număr real atunci mulțimea de adevăr

acestui predicat a indice Pan de

x pe care Haide să o notă mai simplu

cu a este formată din acele elemente

x numere reale cu proprietatea

că x este mai mic decât 5 adică

obținem intervalul minus infinit

5 și acum să vedem care este negația

acestui predicat negația predicatului

pe dx este x mai mare sau egal

decât 5 unde x este număr real

atunci mulțimea de adevăr a negației

acestui predicat este formată din

acele elemente x numere reale cu

proprietatea că x este mai mare

sau egal decât 5 iar această mulțime

este intervalul închis 5 plus infinit

dar această mulțime este de fapt

complementara mulțimii A în raport

cu r putem să evidențiem acest

lucru și pe o axă de exemplu avem

axa numerelor reale fixăm originea

Aici este numărul 5 minus infinit

și plus infinit să Reprezentăm

mai întâi Pe axa mulțimea a adică

intervalul minus infinit 5 este

vorba despre această porțiune hașurată

Deci aceasta este mulțimea A iar

intervalul 5 plus infinit închis

la 5 este această mulțime hașurată

aceasta este complementară mulțimii

A în raport cu mulțimea R Deci

complementară unei mulțimi A în

raport cu o mulțime de este ceea

ce rămâne din D după ce am eliminat

ca să zic așa mulțimea a în continuare

să vedem cum putem să obținem negația

unor propoziții care conțin cuantificatori

Avem două propoziții prima propoziție

pe 1 este vreo poziție universală

oricare ar fi x număr real 2x la

pătrat plus 6 este diferit de 0

pentru a obține negația aceste

propoziții transformăm cuantificatorul

Universal în cuantificatorul existențial

și înlocuim acest predicat cu negația

acestuia Deci negația unei propoziții

universale este o propoziție existențială

prin urmare Haideți să scriem negația

aceste propoziții Nan 1 este următoarea

propoziție există cel puțin un

x număr real astfel încât 2x la

pătrat plus șase să fie egal cu

0 Deci reținem înlocuind cuantificatorul

oricare ar fi cu există iar predicatul

acesta se înlocuiește cu negația

predicatului pentru a obține acum

negația unei propoziții existențiale

procedăm în felul următor cuantificatorul

existențial va fi înlocuit cu cel

Universal iar predicatul se înlocuiește

cu negație acestuia Așadar negația

propoziției pe 2 este următoarea

propoziție oricare ar fi x număr

natural 3x plus 1 este mai mic

decât 0 am văzut și cum putem obține

negația propozițiilor ce conțin

cuantificator și în continuare

să facem câteva aplicații avem

următorul exercițiu să se scrie

negațiile următoarelor propoziții

și Să se determine valoarea lor

de adevăr începem cu propoziția

pe există x număr întreg astfel

încât x plus 3 supra x plus 1 să

fie număr întreg să scriem negația

aceste propoziții am spus că negația

unei propoziții existențiale este

o propoziție universală prin urmare

propoziția anonime se va scrie

astfel oricare ar fi x număr întreg

fracția x plus 3 supra x plus 1

nu aparține lui z Haide să determinăm

și valoarea de adevăr a acestei

propoziții Dacă vom găsi cel puțin

o valoare a lui x pentru care această

fracție să fie număr întreg atunci

propoziția universală va fi falsă

și iată că există o astfel de valoare

de exemplu dacă x este egal cu

unu obținem 4 supra 2 care este

număr întreg prin urmare această

propoziție este falsă Deci valoarea

de adevăr a propoziției Nu nu este

zero trecem la următoarea propoziție

oricare ar fi x număr real 2x minus

8 este mai mare decât 0 negația

acestei propoziții nu nicku există

x numărul real a astfel încât 2x

minus 8 să fie mai mic sau egal

decât 0 dacă găsim cel puțin o

valoare a lui x pentru care această

inegalitate să aibă loc atunci

Propoziția existențială este adevărată

de exemplu dacă x este egal cu

0 minus 8 este întradevăr mai mic

sau egal decât 0 prin urmare Propoziția

existențială este adevărată Deci

valoarea de adevăr a propoziției

non q este unul și ultima propoziție

există x număr întreg astfel încât

3 la x să fie egal cu 27 negația

propoziții r oricare ar fi x număr

întreg 3 la x este diferit de 27

Aceasta este o propozitie falsă

întrucât pentru x egal cu 3 obținem

că 3 la a treia este egal cu 27

deci nu pentru orice valoare x

din sat 3 la x este diferit de

27 Așadar Aceasta este o propoziție

falsă Deci valoarea de adevăr a

propoziției non R este 0 și mai

facem încă un exercițiu Să se determine

mulțimile de adevăr pentru predicatele

p de x q de x negația predicatului

pe dx și negația lui q de x Primul

predicat pe de x radical din 3x

minus radical din 27 mai mic decât

0 unde x este număr real Haideți

mai de să rezolvăm această ecuație

radical din 3x minus radical din

27 mai mic decât 0 radical din

3 x este mai mic decât radical

din 27 împărțim inecuația cu radical

din 3 și obține x mai mic decât

radical din 27 împărțit la radical

din 3 x mai mic decât radical din

9 adică x mai mic strict decât

3 atunci mulțimea de adevăr acestui

predicat a mare indice pdx este

formată din acele elemente x din

R cu proprietatea că x este mai

mic decât 3 adică intervalul minus

infinit 3 Acum putem să obținem

și mulțimea de adevăr pentru negație

acestui predicat și fără să scriem

efectiv negația predicatului am

văzut mai devreme că mulțimea de

adevăr a negației unui predicat

este complementara mulțimii A în

raport cu r în cazul nostru și

atunci Putem să scriem direct mulțimea

de adevăr a negației predicatului

pe aceasta este complementară mulțimii

A în raport cu aer adică intervalul

3 plus infinit închis la 3 următorul

predicat q de x 5 la x plus 2 mai

mare decât 125 să rezolvăm această

inecuația 5 la x plus 2 este mai

mare decât 5 la a treia pentru

că 125 se poate scrie 5 la a treia

în cazul în care avem două puteri

cu aceeași bază atunci inegalitatea

se păstrează și între exponenți

deci putem să scriem că x plus

2 este mai mare decât 3 adică x

mai mare decât 1 prin urmare mulțimea

de adevăr a predicatului q de x

este formată din acele elemente

x din R cu proprietatea x mai mare

decât 1 adică intervalul deschis

1 plus infinit dacă notăm această

mulțime cu b să zicem atunci mulțimea

de adevăr a negației predicatului

q este complementara mulțimii B

în raport cu aer adică intervalul

minus infinit 1 Observați Așadar

că pentru a obține mulțimea de

adevăr a negației unui predicat

nu este obligatoriu să scriem și

negația predicatului