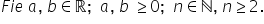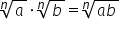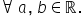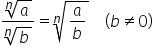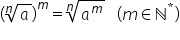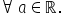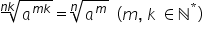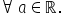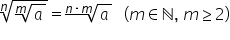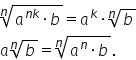Proprietăți ale radicalilor de ordin n

în această lecție o să vedem care

sunt cele mai importante proprietăți

ale radicalilor de ordin n Și începem

cu produsul a doi radicali prima

proprietate radical de ordin n

din a înmulțit cu radical de ordin

n din b va fi egal cu radical de

ordinul n din a ori b Oricare ar

fi a și b numere reale pozitive

cu alte cuvinte produsul a doi

radicali este egal cu radicalul

produsului aceste proprietăți se

pot demonstra foarte ușor Folosind

definiția radicalului de ordin

n și proprietățile puterilor să

vedem un exemplu concret radical

de ordin 3 din 3 ori radical de

ordin 3 din 9 conform proprietății

menționate mai sus vom avea radical

de ordin 3 din 3 ori 9 egal cu

radical de ordin 3 din 27 și egal

cu trei Dacă n este număr natural

impar atunci proprietatea are loc

oricare ar fi numerele reale a

și b a doua proprietate radical

de ordin n din a supra radical

de ordin n din b va fi egal cu

radical de ordin n din a supra

b oricare ar fi numerele reale

a și b pozitive cu b diferit de

0 Așadar câtul a 2 radicali va

fi egal cu radical câtului să vedem

câteva exemple radical de ordin

5 din 96 supra radical de ordin

5 din 3 vom aplica proprietatea

de mai sus și obținem radical de

ordinul 5 din 96 supra 3 egal cu

radical de ordin 5 din 32 și Gal

cu doi un alt exemplu radical de

ordin 3 din minus 1 supra 125 Aplicând

proprietatea de mai sus putem scriem

radical de ordin 3 din minus 1

supra radical de ordin 3 din 125

sau radical de ordin 3 din 1 supra

radical de ordin 3 din minus 125

Așadar acest semn minus poate fi

scris fie la numitor și numărător

egal cu minus 1 supra 5 Dacă n

este număr natural impar atunci

această proprietate are loc oricare

ar fi numerele reale a și b o altă

proprietate pe trei radical de

ordin n din a totul la puterea

M va fi egal cu radical de ordin

n din A la puterea M oricare ar

fi numărul real a mai mare sau

egal cu 0 Așadar ridicarea la putere

a unui radical presupune ridicarea

la putere a expresiei de sub radical

Haideți să demonstrăm această proprietate

voi nutaku pe membrul stâng și

cu q membrul drept fie pe radical

de ordin n din a totul la m și

cu q notăm radical de ordin n din

ala m ne propunem Să arătăm că

pe este egal cu q pentru aceasta

voi ridica fiecare dintre cele

două expresii la puterea n Așadar

avem pe la n egal cu radical de

ordin n din A la puterea M și totul

ridicat la puterea N egal cu radical

de ordin n din ei aici folosind

proprietățile puterilor și avem

m ori and care se mai poate scrie

radical de ordin n din a la puterea

n și totul ridicat la puterea M

dar conform definiție radicalului

de ordin n acest număr radical

de ordin n din a la puterea n va

fi egal cu a la m acum q la n va

fi egal cu radical indice n din

ala m și totul la n conform de

a radicalului radical de ordin

n din un număr ridicat la puterea

n va fi egal cu acel număr de sub

radical Așadar avem egal cu a la

m observăm Așadar capella n este

egal cu q la n și având în vedere

că numerele p și q sunt pozitive

întrucât a a este număr mai mare

sau egal cu 0 rezultă din această

relație că p este egal cu q așa

dar am demonstrat această proprietate

să vedem cum putem să o aplicăm

concret în exerciții un prim exemplu

radical indice 3 din 7 ridicat

la puterea a patra a fi egal cu

radical de ordin 3 din 7 la a patra

egal în continuare cu radical de

ordin 3 din 7 la a treia ori 7

și Aplicând proprietatea pe 1 putem

scrie egal cu radical de ordin

3 din 7 la a treia înmulțit cu

radical de ordin 3 din 7 dar radical

de ordin 3 din 7 la a treia este

egal cu 7 ori radical de ordin

3 din 7 un alt exemplu radical

din 4 la a treia conform relației

de mai sus vom putea scrie egal

cu radical din 4 totul ridicat

la puterea a treia radical din

4 este 2 la a treia și egal cu

8 în alt exemplu radical indice

3 din 8 la a patra va fi egal cu

radical indice 3 din 8 totul la

puterea a patra egal cu 2 la a

patra și Eden cu 16 trecem la următoarea

proprietate aceasta se referă la

simplificarea ordinului și exponentului

puterii expresiei de sub radical

pe 4 are loc următoarea relație

radical indice n k din a la m k

va fi egal cu radical indice n

din a m oricare ar fi numărul pozitiv

a am simplificat Așadar ordinul

radicalului și exponentul puterii

expresiei de sub radical un exemplu

radical de ordin 5 din 2 la puterea

a 15-a va fi egal cu radical de

ordin 5 din 2 la 5 ori 3 simplificăm

cu 5 și vom obține 2 la a treia

adică 8 un alt exemplu b radical

de ordin 6 din 4 la 5 Încercăm

să exprimăm ordinul radicalului

și exponentul numărului de sub

radical cu ajutorul aceluiași număr

pentru a putea face apoi simplificări

6 este 2 ori 3 iar 4 este 2 la

a doua și totul la a cincea va

fi egal cu radical indice 2 ori

3 din 2 la 2 ori 5 aici folosind

proprietățile puterilor Acum putem

simplifica cu 2 și ne rămâne radical

indice 3 din 2 la a cincea Care

este egal cu radical indice 3 din

32 acestea au fost două exemple

în care am simplificat radicalii

iar operația inversă se va numi

amplificarea radicalilor trece

mai departe la proprietatea a cincea

și anume extragerea radicalului

dintre un alt radical radical de

ordin n din radical de ordin n

din a va fi egal cu radical de

ordin n ori m din a oricare ar

fi numărul pozitiv a Așadar pentru

a extrage un radical din alt radical

se extrage radicalul de ordin egal

cu produsul ordinelor de exemplu

radical de ordin 3 din radical

din 10 radicalul mai mic are ordinul

2 care nu se scrie De obicei Așadar

vom avea radical de ordin 3 ori

2 din 10 și egal cu radical de

ordin 6 din 10 în alta exemplu

radical de ordin 5 din radical

de ordin 3 din minus 7 va fi egal

cu radical de ordin 5 ori 3 din

minus 7 egal cu radical de ordin

15 din minus 7 Dacă m și n sunt

numere impare observăm că proprietatea

are loc pentru orice număr real

a și o ultimă proprietate discutăm

despre scoaterea și introducerea

factorilor sub radical mai întâi

să vedem cum putem să scoatem factorii

de sub radical radical de ordin

n din a la n k ori b aplicăm proprietatea

pe 1 produsul radicalilor și vom

avea radical de ordin n din a la

n k ori radical de ordin n din

b egal în continuare cu radical

de ordin n din a la k totul la

n ori radical de ordin n din b

conform definiției radicalului

primul Factor va fi egal cu a la

k și avem la decal de ordin n din

b un exemplu radical indice 3 din

40 vom încerca să scriem numărul

40 ca un produs de doi factori

dintre care unul să fie la puterea

a treia pentru a putea apoi să

scoatem de sub radical 40 este

egal cu 8 ori 5 la am scris așa

deoarece 8 este puterea a treia

a lui 2 și va fi egal în continuare

cu radical de ordin 3 din 2 la

a treia ori 5 egal cu radical de

ordin 3 din 2 la a treia ori radical

de ordin 3 din 5 și egal cu 2 radical

de ordin 3 din 5 introducerea factorilor

sub radical se va face după formula

a radical de ordin n din b egal

cu radical de ordin n din a la

n ori b Oricare ar fi a și b numere

reale pozitive de exemplu 2 radical

de ordin 5 din 3 va fi egal cu

radical de ordin 5 din 2 la a cincea

ori 3 egal cu radical de ordin

5 2 la a cincea este 32 ori 3 și

egal cu radical de ordinul 5 din

96 Toate aceste proprietăți le

vom aplica în lecțiile următoare

atunci când mo face operații cu

radicali