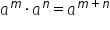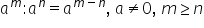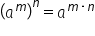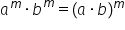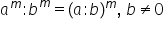Reguli de calcul cu puteri
Tag-uri
Partajeaza in Google Classroom

Transcript
să vedem acum Care sunt regulile
de calcul cu puteri și mai înainte
Haide să vedem ce este aceea o
putere să ne reamintim și avem
aici un exemplu 2 la a cincea Ce
înseamnă asta înseamnă că trebuie
să avem un produs de cinci factori
toți egal cu doi Deci avem 2 înmulțit
cu 2 înmulțit cu 2 înmulțit cu
2 trebuie să scriem pe doi de cinci
ori am scris de patru ori mai scriem
încă o dată bun cât obținem pe
aici avem patru și aici 4 4 x 4
în de 16 ori 2 ne dă 32 foarte
mare atenție acum să nu fim tentați
să spunem că 2 la a cincea ne de
2 ori 5 pentru că aici nu avem
produsul 2 ori 5 2 la a cincea
ne dă 32 în timp ce 2 ori 5 ne
dă 10 Deci clar vorbim de numere
diferite bune am amintit Cum se
calculează o putere ce denumiri
folosim Iată doi poartă numele
de bază de ce apare jos se numește
bază în timp ce numărul care este
scris deasupra și este mai mic
se numește exponent și acum Haideți
să descoperim gradat să găsim regulile
de calcul cu puteri Și începem
de la un exemplu vrem să scriem
ca o singură putere acest produs
3 la a doua înmulțit cu 3 la a
cincea bun atunci Haideți să calculăm
Deci 3 la a doua înmulțit cu 3
la a cincea ce vom face Păi 3 la
a doua înseamnă că trebuie să ne
apară factorul 3 scris de două
ori de notăm 3 înmulțit cu 3 înmulțit
mai departe îngroșa și acest punct
aici cu 3 la a cincea Deci scriem
acum pe trei de cinci ori avem
trei ori trei ori trei ori trailer
scrise de 1 2 3 4 ori înmulțit
cu 3 și acum Hai să facem calculul
si obține observăm că peste tot
avem factori Câți factori sunt
1 2 3 4 5 6 7 Deci avem șapte factori
toți egal cu 3 pe de fapt avem
puterea 3 la a șaptea acum de unde
îl am obținut pe De unde de unde
am obținut exponentul 7 poiată
avem aici doi factori amândoi egal
cu 3 iar Aici avem cinci factori
toți egali cu trei pui de fapt
doi factori adunat cu cinci factori
ne dă șapte factori cu alte cuvinte
pe șapte la Moftinu de fapt din
suma doi plus cinci Deci avem trei
la exponentul acesta doi plus cinci
Adică am adunat de fapt exponenții
care e regula prin urmare când
trebuie să înmulțim două puteri
care au aceeași au mai multe puteri
care au aceeași bază Scrie în baza
Deci copie în baza și adunăm exponenții
2 plus 5 și rezultatul este 3 la
a șaptea Haideți să facem și alte
exemple să calculăm acum 5 sau
Haideți să facem ceva mai simplu
2 la a doua înmulțit cu 2 la a
treia ori 2 la a opta Bun deci
factorul 2 trebuie să ne apară
de două ori și Avem așa 2 înmulțit
cu 2 înmulțit mai departe cu Deci
înmulțit factorul 2 înscriem acum
de trei ori Deci avem doi ori doi
ori doi înmulțit cu este cel mai
mult cu trebuie să avem un produs
de opt factori egal cu doi Acum
deci înscriem pe doi de opt ori
o dată de două ori de trei ori
de patru ori de cinci ori de șase
ori de șapte ori de opt ori da
Iată 1 2 3 4 5 6 7 8 și să vedem
cât vom obține pe aici Avem doi
factori aici avem trei factori
iar Aici am notat 8 factori toți
egal cu 2 Care este baza acestei
puteri Este clar că este 2 și ce
trecem la exponent Păi avem doi
factori cu trei factori cu opt
factori de chanttal 2 plus 3 plus
8 cu alte cuvinte am adunat de
fapt acest exponenți și obținem
așa 2 la 2 Haideți să scrie în
baza 2 cu 3 ne dă 5 cu 8 13 Deci
2 la puterea 13 exponentul 13 încă
un exemplu 5 înmulțit cu 5 la a
noua înmulțit cu 5 la a doua ori
5 la a treia este egal cu un acumula
vem aici trecut pe 5 Cum îl putem
scrie ca o putere Păi întotdeauna
orice număr poate fi scris ca o
putere cu exponentul 1 5 la întâia
înseamnă De fapt cinci cum avem
aici produse de puteri care au
toate aceeași bază atunci copii
în baza și adunăm exponenții 1
plus 9 plus doi plus trei și vom
obține 5 la aici obținem 10 cu
5 adică 15 5 la puterea la exponentul
15 Dacă ar fi să scriem și o regulă
când înmulțim două sau mai multe
puteri care au aceeași bază deci
a la m înmulțit cu a Lion putem
avea produse de oricât de multe
puteri dorim condiția ca ele să
aibă aceeași bază atunci ce facem
copiem bază și adunăm exponenții
m plus n aceasta este regula care
ne va ajuta foarte mult în calcul
atunci când vorbim de produse de
puteri cu aceeași bază pentru următoarea
regulă de calcul Haide să începem
de la această împărțire 2 la a
cincea împărțit la 2 la a doua
și vrem să scriem ca o singură
putere rezultatul acestei împărțiri
Deci avem așa doi la cincea împărțit
la 2 la a doua și să calculăm 2
la a cincea înseamnă că avem cinci
factori toți egal cu doi Deci doi
ori doi ori doi ori doi ori doi
la înscris pe doi de cinci ori
împărțit la 2 la a doua adică împărțit
la produsul 2 ori 2 bun am scris
corect nu de ce nu am notat corect
aici pentru că lăsăm scrierea Așa
se înțelege că acest produs se
împarte la 2 iar rezultatul se
înmulțește apoi cu 2 ceea ce este
fals pentru că Iată acest produs
care înseamnă 2 la a cincea se
împarte de fapt la 2 la a doua
adică la produsul 2 ori 2 deci
ce trebuie să trecem trebuie să
trecem aici paranteze Aici nu e
neapărat nevoie să trecem vreo
paranteză însă noi știm că înmulțirea
este asociati deci putem să grupăm
factorii după cum dorim cum ar
fi mai ușor să îi grupăm Păi am
putea de exemplu să grupăm pe aceștia
doi pentru că având aici un produs
urmat de om părți repute să facem
mai întâi împărțirea și ușor să
facem această împărțire sigur avem
un număr împărțit la el însuși
că avem aici 4 împărțit la 4 Deci
ne dă 1 cât vom obține păi avem
2 înmulțit cu 2 înmulțit cu 2 înmulțit
cu aceste rezultat care ne arată
unu știind că numărul unu nu influențează
produsul Deci chiar putem să îl
ștergem și ce avem la rezultat
Avem doi ori doi ori doi adică
doi la a treia cum am obținut exponentul
3 băiat am avut aici cinci factori
aici am avut doi factori și nu
au rămas De fapt trei factori cu
alte cuvinte 3 se obține de fapt
din diferența 5 minus 2 iar 5 minus
2 care ar fi regula atunci când
împărțim două puteri toți sau mai
multe puteri care au aceeași bază
copiem bază și scădem exponenții
5 minus 2 și am obținut 2 la exponentul
3 Haideți acum să facem alte exemple
să calculăm 3 la a patra împărțit
la 3 la a treia evident că putem
să calculăm prin diferite moduri
Haideți să vedem cum e mai simplu
3 la a patra înseamnă 81 de ar
trebui să știm Cât face 3 la a
patra să calculăm împărțit la 3
la a treia dacă facem calcul ne
dă 27 81 împărțit la 27 facem împărțirea
și ne dă 3 dacă aplicăm această
regulă pe care am învățat tu aici
Ce observăm avem puteri cu aceeași
bază și între ele operația de împărțire
Deci copiii în baza 3 și scădem
exponenții 4 minus trei și obținem
3 la întâia care înseamnă de fapt
trei pe care modalitate de calcul
a mai ușoară e clar aceasta este
mult mai simplu mult mai simplă
bun încă un exemplu să calculăm
Acum șapte la 24 împărțit la șapte
la a treia împărțit la 7 la 19
egal cu cum avem puteri cu aceeași
bază peste tot avem operația de
împărțire copiii în baza și scădem
exponenții 24 minus 3 minus 19
și facem calculul avem șapte la
24 minus 3 ne dă 21 minus 19 ne
dă doi șapte la a doua adică 49
avem șapte ori șapte un Haideți
să scriem atunci și regula când
împărțim două sau mai multe puteri
cu aceeași bază de exemplu a la
m împărțit la a la n atunci copiii
în baza și scădem exponenții m
minus n aici mai trebuie să trecem
condiția ca ei să fie diferit de
0 nu pot să împărțim la un număr
când el este 0 și m să fie mai
mare decât n că avem aici Diferența
a minus a e mai mare sau egal cu
n Deci încadrăm aceasta este regula
de calcul și acum pentru următoarea
regulă pornind de la acest calcul
te fac vrem să scriem ca o singură
putere 2 la a treia totul la a
cincea bun pe avem de fapt această
putere adică acest număr ridicat
la exponentul 5 Deci acest număr
îl scriem de cinci ori și Avem
doi la a treia înmulțit cu 2 la
a treia înmulțit cu 2 la a treia
și așa mai departe trebuie să îl
trecem de cinci ori Iată 1 2 3
4 5 bun peste tot avem produse
de puteri care au aceeași bază
Deci copiem bază și ce facem cu
exponenții fiind vorba de produse
aici Îi vom aduna de câte ori ne
apare 3 Păi de cinci ori că sunt
cinci factori Deci avem 3 plus
3 plus 3 plus 3 plus 3 la masa
de 5 ori da Bun deci am obținut
2 la ce exponent Păi dacă îl adunăm
pe 3 de cinci ori înseamnă de fapt
3 înmulțit cu 5 Păi ia să vedem
Am plecat de aici 2 la a treia
totul la a cincea egal cu 2 la
3 ori 5 Ce am făcut cu exponenții
cheamă înmulțit Deci când ne apara
astfel de puteri în care avem această
paranteză atunci vom copia bază
și vom înmulțire exponenții 3 ori
5 adică ne dă doi la 15 un alt
exemplu să calculăm acum 3 la a
doua totul la a doua mai scrie
în baza 3 și înmulțim exponenții
doi ori doi doi ori doi adică ne
dă trei la a patra sau 5 la a treia
totul la am optat de exemplu avem
cinci la trei ori 8 Adică ne dă
cinci la 24 sau 2 la a 7-a totul
la a doua ce avem așa doi la 7
ori 2 înmulțim exponenții adică
2 la 14 pun aici putem să facem
și observație și să facem aici
semnul exclamării vrem să calculăm
acum 2 la 7 la a doua deci nu 2
la a șaptea totul la a doua și
2 la 7 la a doua Păi de fapt aici
în primul rând observăm că nu ne
mai apar paranteze și această bază
2 este ridicată la exponentul 7
la a doua Deci nu are sens să înmulțim
aici pe 7 cu 2 cana ceastă situație
pentru că vorbim de 7 la a doua
cu alte cuvinte ca să facem acest
calcul Scrie în baza 2 și ridicăm
la putere pe 77 la a doua înseamnă
49 de ceartă că vorbim de lucruri
diferite 2 la 7 la a doua nu este
același lucru cu doi la șaptea
totul la a doua aici obținem 2
la 49 iar Aici iar 2 la 14 Dacă
ar fi să scriem și regula la m
totul la n Nevada Scrie în baza
ei și înmulțim exponenții m ori
n iar aceasta este regula acum
Haideți să scriem ca o singură
putere produsul 12 la a doua ori
3 la a doua de fapt 12 la a doua
ori 3 la a doua Vrem să vedem ce
obținem atunci când înmulțim puteri
care au același exponent Nu ne
interesează dacă bazele sunt diferite
și importante să avem același exponent
Păi 12 la a doua Avem 12 ori 12
înmulțit mai departe cu 3 la a
doua adică cu trei ori trei bun
însă înmulțirea este Cum este și
asociativă și comutativă deci putem
să grupăm factorii așa cum dorim
și îi putem nota 12 ori trei Ioan
grupat aceștia a 2 înmulțit cu
cine a rămas adică 12 ori 3 bun
însă putem să continuăm Gruparea
și grupăm pe primii doi și pe ultimii
doi de fapt avem acest produs 12
ori 3 ridicat la ce putere la puterea
a doua apare de două ori acest
produs si am obținut Păi Iată de
fapt înmulțim bazele 12 ori 3 totul
ridicat la exponentul 2 evident
că uneori ne e mai ușor să folosim
această scriere sau poate aceasta
de exemplu dacă ni se dă un produs
de numere și noi la un exponent
și noi vrem să desfacem acel produs
atunci exponentul merge să spunem
așa la fiecare vază în parte la
am distribuit pe doi și pe la 12:00
și la 3:00 sau poate că uneori
ni se dă această scriere de exemplu
avem cinci ori 11 ori 3 totul ridicat
la a patra și vrem să desfacem
acest produs și vom avea 5 la a
patra înmulțit cu 11 la a patra
înmulțit cu 3 la a patra dacă ar
fi să scriem regula avem că a la
m ori b Deci nu contează bază important
este să avem același exponent de
ciorbe la m este egal de fapt cu
a orbi înmulțim bazele totul la
exponentul m aceeași regulă are
loc și în cazul în împărțirii Deci
dacă avem 12 la a doua împărțit
la 3 la a doua si vom obține atunci
pe Avem 12 la a doua împărțit la
3 la a doua o explicație o putem
considera aceasta 12 la a doua
Deci notăm 12 ori 12 împărțit la
3 la a doua adică la produsul 3
ori 3 atenției și trebuie să trecem
paranteza acum am discutat pe 12
îl putem Scrie patru ori trei Deci
avem patru ori 3 înmulțit cu din
nou patru ori 3 împărțit la 3 ori
3 acum acești factori putem grupa
îi putem grupat tot așa după cum
am după cum dorim Deci patru ori
patru putem să îi grupăm astfel
înmulțit cu cine a rămas adică
3 ori 3 împărțit la 3 înmulțit
cu 3 și acum Avem un produs pentru
că pe aceste putem grupa Deci avem
un produs urmat de om părți repute
să facem mai întâi împărțirea și
aici obținem 1 avem 9 împărțit
la 9 de unu cu alte cuvinte Rezultatul
este 4 x 4 Cum la muți Noot pe
4 pe 4 înseamnă de fapt 12 împărțit
la trei Avem 12 împărțit la 3 înmulțit
tot cu 12 împărțit la trei iade
obținem de fapt 12 împărțit la
3 totul la exponentul 2 adică scriem
vasele Deci 2 10 împărțit la trei
și vom trece acest această împărțire
la exponentul comun adică la exponentul
2 iar de foarte asemănătoare cu
această regulă doar că în loc de
înmulțire avem operația de împărțire
deci a la e m împărțit la b tot
la m este egal cu a împărțit la
b totul la exponentul e aici trebuie
să mai trecem că b să fie un număr
natural diferit de 0 pentru că
împărțim la un număr și el trebuie
să fie nenul Deci Iată am mai găsit
încă două reguli de calcul cu puteri