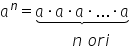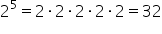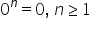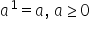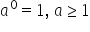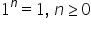Puterea cu exponent natural a unui număr natural
Tag-uri
Partajeaza in Google Classroom
Transcript
în continuare vom învăța despre
puterea cu exponent natural a unui
număr natural și ai de să începem
cu ceva cunoscut și să facem acest
calcul Avem doi plus doi plus doi
Putem să scriem Mai simplu această
sumă sigur Avem doi ori trei și
obținem rezultatul 6 dacă însă
în loc de operația de adunare trecem
înmulțire vom avea doi ori doi
înmulțit cu doi e bine și această
scriere are o notație prescurtată
și anume Voice aici 2 și deasupra
vom trece un 3 mai mic și citim
2 la puterea a treia sau mai simplu
2 la a treia cât obținem Păi 2
ori 2 4 ori 2 8 si am obținut aici
2 la a treia reprezintă de fapt
puterea cu exponent natural unui
număr natural și acum mare atenție
2 la a treia nu este același lucru
cu 2 ori 3 și poate că unii dintre
voi sunteți tentați să faceți acest
calcul Când plătesc 2 la a treia
să spuneți a bun este egal cu 2
ori 3 nu e adevărat 2 la a treia
este 8 în timp ce 2 ori 3 este
6 clar vorbim de numere diferite
ce denumiri folosim numărul care
apare aici se numește baza baza
puterii iar numărul de deasupra
se numește exponent exponentul
puterii poate că în manuale veți
întâlnim și această formulă a la
puterea n unde a și Elsa numere
naturale n mai mare sau egal cu
2 cu cât este egal avem de fapt
a înmulțit cu a înmulțit cu ei
și așa mai departe înmulțit cu
ei de câte ori de n mic ori puteți
evidență rețineți această formulă
care descrie regula de calcul a
puterilor și acum Haideți să facem
un continuare și alte exemple și
să luăm de exemplu 3 la puterea
a doua ce avem Păi numărul de aici
adică bază ne arată factorul care
apare la înmulțire Iar exponentul
ne arată de câte ori scriem acest
Factor adică avem 3 înmulțit cu
3 care ne dă nouă din nou atragem
atenția asupra faptului că trei
la a doua nu este același lucru
cu 3 ori 2 Păi să calculăm 3 la
a doua este 9 am văzut de Tion
Timiș si 3 ori 2 este 6 klar vorbim
de numere diferite încă un exemplu
să facem acum 3 la a treia avem
de fapt pe 3 înmulțit cu 3 înmulțit
cu trei Da deci factorul 3 ne apare
de trei ori și avem trei ori trei
nouă ori 327 bun iar Haide să trecem
aici semnul de exclamare pentru
că 3 la a treia nu este același
lucru cu trei ori 327 nu este același
lucru cu 9 încă un exemplu am avut
trei la a doua 3 la puterea a treia
să facem și trei la puterea a patra
Ce trebuie să facem în trei trebuie
să apară scris ca factori Și luăm
scrie de patru ori Deci trei ori
trei ori trei și mai trebuie încă
o dată ori trei avem unu doi trei
patru factori toți egali cu trei
cât obține Păi 3 ori 3 ne dă nouă
înmulțit cu 9 adică 81 iar și ușor
de văzut faptul că trei la a patra
nu e același lucru cu 3 ori 4 aici
avem 81 în timp ce aici Avem 12
un alt exemplu să calculăm 5 la
puterea a doua bază este 5ar exponentul
este 2 si trebuie să facem factorul
5-a par scris de două ori Deci
avem 5 înmulțit cu 5 și obținem
25 din nou facem observația că
cinci la a doua nu este același
lucru cu 5 înmulțit cu 2 aici obținem
25 în timp ce aici avem cinci ori
doi adică în 10 klar vorbim de
numere diferite să calculăm acum
și 5 la a treia pe avem așa pe
5 trebuie să îl înmulțim trebuie
să apară ca Factor de trei ori
de ce avem cinci ori cinci ori
cinci cinci ore cinci ne dă 25
înmulțit cu 5 ne dă 125 iarăși
Haide să scriem cinci la a treia
este de De ce produs de produsul
5 înmulțit cu 3 aici avem 125 în
timp ce aici avem 15 avem numere
diferite si ușor de observat în
folosind una de aceste exemple
în cazul puterilor numerele cresc
mult mai rapid Iată cinci la a
doua 25 5 la a treia deja 125 în
timp ce în aceste situații creșterea
este mult mai lentă de la 10:00
am ajuns la 15:00 deci putem să
reținem faptul că atunci când vorbim
de puteri a vorbim de o creștere
rapidă încă un exemplu Patrula
7-a bază este 4 exponentul este
7 Vrem ca factorul 4 să ne apară
scris De câte ori de șapte ori
Deci avem 4 ori 4 ori 4 înmulțit
cu 4 înmulțit cu 4 câte avem unul
2 3 4 5 ne mai trebuie 2 ori 4
x 4 deci am scris factorul 4 de
șapte ori nu vom face calculul
acestui număr natural este un număr
mare dar putem să punem întrebarea
Oare patru la a șaptea este egal
cu 4 înmulțit cu 7 nu vorbim clar
de numere diferite pentru că 4
la a șaptea se vede cu ușurință
că este un număr mult mai mare
decât 47 Adică decât 28 Haideți
acum să facem câteva exemple de
puteri care au baza 0 să calculăm
0 la 2015 alte cuvinte trebuie
să scriem factorul 0 de 2015 ori
ce avem așa zero înmulțit cu 0
înmulțit și așa mai departe înmulțit
cu 0 aici avem 2015 factori Care
este rezultatul știind că orice
numar înmulțit cu 0 ne dă 0 Deci
0 la 2015 na dat în zero punct
Dar cât o fi atunci și zero la
a doua pe zero trebuie să îl trecem
ca Factor de două ori zerouri zero
adică ne dă 0 la fel se întâmplă
și cu zero la a treia și așa mai
departe De fapt 0 la orice putere
Haideți să notăm acele exponent
cu n ne dă 0 oricare ar fi n un
număr natural mai mare sau egal
cu unu nu am scris aici 0 la puterea
întâi pe zero la întâia Ce înseamnă
că trebuie să îl scriem pe 0 nu
de 2015 ori că aici e o singură
dată egal cu 0 că tot a venit vorba
de nume cu de puteri cu exponentul
1 Haide să vedem Cu cât este egal
2 la a întâia 2 la Antonia înseamnă
că trebuie să scriem factorul 2
o singură dată deci ne dă doi Cât
este 3 la întâia Păi ne dă trei
la fel Patrula întâi ani de 4 și
așa mai departe analog și unul
la exponentul 1 ne dă tot unul
Deci ID să scriem și această regulă
Că un număr natural ridicat la
exponentul 1 adică a am trecut
numărul natural respectiv la notat
cu a ridicat la exponentul 1 ne
dă întotdeauna Cât Păi doi la unu
ani a dat doi trei la întâi ani
a dat 3 Deci alaltă iau să ne dea
a Oricare ar fi a un număr natural
chiar Putem să scriem mai mare
sau egal cu 0 am văzut că dacă
a este 0 avem 0 la întâia Iată
care ne dă 0 Deci era egal cu zero
Am discutat de puteri care au baza
a0 ce se întâmplă însă când avem
exponentul egal cu 0 pe aici să
vedem Cu cât este egal 2 la puterea
0 și nu vom da aici o explicație
riguroasă din punct de vedere matematici
mai multe una intuitivă și pentru
aceasta vom calcula succesiv 2
la a patra 2 la a treia 2 la a
doua în Deci observăm cu exponenți
descresc 2 la a întâia și 2 la
0 2 la a patra Cu cât este egal
Avem doi trebuie să apară factorul
2 de patru ori de și doi ori doi
ori doi ori doi avem patru înmulțit
cu 4 adică 16 2 la a treia avem
2 înmulțit cu 2 înmulțit cu doi
doi apare de trei ori și ne dă
8 2 la a doua avea doi ori doi
adică patru Haide să notăm aici
Deci 16 urmă atât de 8 aici avem
patru și aici Avem doi la unu am
văzut este 2 și trebuie să vedem
cât este 2 la 0 Ce observăm pentru
a ajunge de la 16:00 la 18:00 am
împărțit de fapt la 2:00 de la
8:00 la 4:00 trebuie să împărțim
la doi de la 4 la 2 din nou împărțim
la doi deci de la 2 la 2 la 0 trebuie
să împărțim în continuare la 2:00
asta înseamnă că să ștergem aici
2 împărțit la 2 ne dă de fapt unu
cu alte cuvinte 2 la 0 este egal
cu 1 putem să ștergem semnul de
întrebare și venim și notăm egal
1 Haide să ștergem aici și să scriem
regula pe care am obținut o și
anume că orice număr ridicat la
puterea 0 pentru că Iată și 3 la
0 este 1 și 4 la 0 este 1 Da deci
a la puterea 0 este egal cu 1 oricare
ar fi n număr natural mai mare
sau egal cu 1 și 1 la 0 ne dă tot
1 vedeți că aici am evitat cazul
în care a este egal cu 0 nu a scris
ca mai sus a mai mare sau egal
cu 0 ce am trecut am mai mare sau
egal cu ce se întâmplă când avem
0 la 0 Haide să vedem în această
situație 0 la puterea 0 Cu cât
este egal poate unii dintre voi
ați putea să îmi spuneți că ne
ghidăm după această regulă pentru
că 0 la en adizero înseamnă că
și 0 la 0 ne dă tot zero Deci 0
la 0 egal 0 sau alții ar putea
să îmi spună că ne ghidăm după
această regulă 0 la 0 ne dă de
fapt 1 Deci 0 la 0 poate să fie
egal și cu unu să știți că și matematicienii
au păreri împărțite în ceea ce
privește acest caz de 0 la 0 De
aceea pentru că încă rămâne un
semn de întrebare aici spunem că
acest caz este unul nedefinit Bon
Prix urmare Haideți să reținem
aceste reguli prima regulă care
ne spune că 0 la n este 0 oricare
ar fi exponentul un număr natural
diferit de 0 a la exponentul 1
este a oricare ar fi n număr natural
orice Expo orice bază ridicată
la puterea 0 ne dă 1 atâta timp
cât baza nu este 0 pentru că 0
la 0 este un caz nedefinit și dacă
vrei să mai putem să adăugăm o
regulă foarte simplă cu cât este
egal 1 la unt exponent Păi trebuie
să avem de fapt factori toți egal
cu 1 și să avem în factori 1 lor
unu unu și așa mai departe De fapt
ne dă 1 oricare ar fi exponentul
n mai mare sau egal cu 0 am văzut
că unu la zero Iată ne dăm unul
poate cuvinte Haide să reținem
aceste reguli pe care le am scris
și să reținem și Cum calculăm o
putere de exemplu 2 la a cincea
nu este egal cu 2 ori 5 Ce înseamnă
doi ori doi ori doi ori doi scriem
numărul 2 de cinci ori și rezultatul
este 32