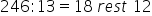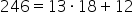Teorema împărțirii cu rest

în continuare vom efectua câteva

aplicații ale teoremei împărțirii

cu rest Cine spune teorema împărțirii

cu rest ne spune că ori De câte

ori împărțind două numere naturale

adică avem deîmpărțitul împărțit

la împărțitor vom obține alte două

numere naturale unice care reprezintă

de fapt câtul și restul e bine

teorema împărțirii cu rest ne spune

că deîmpărțitul este egal cu produsul

dintre împărțitor și cât adunat

cu restul și restul este un număr

natural mai mare sau egal cu 0

și întotdeauna strig mai mic decât

împărțitorul Un neam amintit și

teorema împărțirii cu rest și acum

Haide să trecem la treabă vrem

să determinăm numărul natural care

împărțit la 8 dă câtul 10 și restul

7 Păi Haideți să notăm acest număr

natural pe care îl căutăm cu el

mult noi știm că n împărțit la

8 Deci n împărțit la 8 dă cîtul

10 notăm este egal cu 10 și restul

7 rest 7 cum a spus și înainte

avem aici deîmpărțitul 18 este

câtul iar restul este 7 pardon

Haide să scriem aici rest ce facem

acum teorema împărțirii cu rest

de spune că deîmpărțitul egal cu

produsul dintre împărțitor și cât

adunat cu restul Deci plus rest

același vom face și noi aici avem

că deîmpărțitul Adică n se poate

scrie ca fiind împărțitorul ori

câtul Deci 8 ori ce adunat cu restul

Păi e clar că putem să determinăm

pe an și avem că n este 8 ori 10

adică 80 plus 7 n este egal cu

87 dacă vrei să facem și verificarea

Haide să notăm aici și VF de la

verificare Vrem să vedem dacă întradevăr

numărul 87 împărțit la 8 ne dă

întradevăr câtul 10 și restul 7

pe 8 intră în 8 o singură dată

unu opt opt facem scăderea coborâm

pe șapte acum în acest moment nu

putem spune că 7 este restul împărțirii

pentru că trebuie să vedem de câte

ori se cuprinde 8 în 7 și el se

cuprinde de zerouri zerouri 8:00

ne dă 0 acum scădem 7 minus 07

mai avem Ce cifră să coborâm de

la deîmpărțit nu a bine în acest

moment putem Spune Că întradevăr

am obținut restul și câtul 10 cu

alte cuvinte numărul căutat este

87 să aflăm toate numerele naturale

care împărțite la 4 dau câtul 9

De ce credeți că ne apare în enunț

cuvântul toate pentru că e posibil

să fie mai multe numere naturale

care împărțite la 4 dau câtul nouă

de aceea Haideți să alegem unul

din aceste numere și să îl notăm

cu n cu alte cuvinte vrem să îl

găsim pe n care împărțit la 4 Deci

notăm de câtul 9 bun și Cât este

restul pentru că iată în enunț

nu se spune nici că este o împărțire

exactă însă nu știm nici restul

împărțirii asta înseamnă că restul

trebuie să determinăm noi de ce

ai de să notăm așa rest aer Ce

știm noi conform teoremei împărțirii

cu rest pe știind că deîmpărțitul

este egal cu produsul dintre împărțitor

și cât Deci avem patru ore 9 adunat

cu restul pe care ia pe nu îl cum

Ce observăm De ce avem nevoie ca

să determinăm pe el Păi ne trebuie

valoarea restului știm noi ceva

despre rest sigur știind că restul

este un număr natural mai mare

sau egal cu 0 și este strict mai

mic decât împărțitorul Adică decât

patru păi Care sunt numerele naturale

mai mari sau egale cu 0 și strig

mai mici ca 4 ușor să le determină

pe ceai de să notăm că ieri ia

valorile 0 1 2 și 3 Deci poate

să fie fie zero și unu fie doi

fie trei și acum trebuie să luăm

fiecare situație în parte Câte

valori vom obține pentru n4 valori

diferite pentru că Iată avem patru

valori distincte pentru aer să

notăm dacă este egal cu zero adică

prima situație ce vamă rezultă

că e n Nevada patru ori nouă adică

36 adunat cu restul Care este zero

deja am trecut aici adică 36 dacă

însă restul este egal cu 1 vom

obține că e n ne dă 36 plus unu

Iată la aici adică 37 Dacă restul

Însă este 2 avem că n este egal

cu 36 adunat cu doi Haideți să

ștergem aici ca să se vadă să îl

așezăm în același loc Deci adunat

cu doi și avem că este egal cu

38 și în final Dacă restul este

egal cu 3 rezultă că e n ne dă

36 plus trei adică 39 cu alte cuvinte

numerele care împărțite la 4 dau

câtul 9 sunt trei și 6 37 38 și

39 de voi scrie aici 36 37 38 și

39 Suma a două numere naturale

este 62 să determinăm numerele

știind că prin împărțirea numărului

mare la cel mic se obține câtul

cinci și restul doi câte numere

avem De determinat trebuie să determinăm

două numere naturale a căror sumă

este 62 atunci Haide să notăm că

a plus b a și b fiind numerele

căutate suma lor este 62 Ce mai

știm că dacă împărțim numărul mare

la cel mic Păi asta înseamnă că

trebuie să facem o alegere Haide

să consideram ca este strict mai

mare decât b puteam să facem și

invers b este mai mare decât a

nu are importanță știind că dacă

îl împărțim pe a la b de să notăm

a împărțit la b ne dă câtul 5 și

restul este 2 Ce știm conform teoremei

împărțirii cu rest cum putem scrie

această relație deîmpărțitul adică

a este egal cu produsul dintre

împărțitor și cât de ce avem b

ori 5 plus restul Care este 2 si

facem acum e bine pe baza acestor

două relații trebuie să determinăm

și pe a și pe b putem să îl exprimăm

pe a în funcție de B sigure deja

este exprimat Iată că a este egal

cu b ori cinci plus doi această

expresie o vom trece de fapt în

locul lui A deci pe a din prima

relație îl înlocuim Cu ce avem

aici pentru că b ori 5 plus 2 este

egal de fapt cu ei și vom avea

așa b înmulțit cu cinci plus doi

la întrecut pe ei Da plus b este

egal cu 62 alte cuvinte ce am obținut

o ecuație cu necunoscuta a b Păi

Haideți să determinăm pe b Cât

de B avem aici avem b ori 5 adică

5 de b cu un b înseamnă că avem

șase de bbc6 înmulțit cu B plus

2 ca acest termeni a rămas este

egal cu 62 ce facem în continuare

Păi trebuie să determinăm mai întâi

Cât este 6 ori pe pentru aceasta

din relație scădem pe 2 sau altfel

spus trecem pe doi Peste egal cu

semn schimbat Deci vom avea de

șase ori b este egal cu 62 minus

doi șase ori b ne dă 60 b este

egal cu 60 împărțit la șase adică

bn de 10 ceartă că am de terminat

pe b Cum găsim pe A păi tu Înlocuim

pe b în prima relație sau în cea

de a doua oricare variantei corectă

dacă folosim a doua relație avem

că a este 10 înmulțit cu 5 plus

2 facem calcului și obținem 50

plus doi adică 52 cu alte cuvinte

am obținut că numărul b este egal

cu 10 iar numărul a este egal cu

52 evident că suma a plus b e ușor

de văzut ne de 62 și dacă facem

52 împărțit la 10 vom obține 5

rest 2
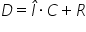