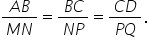Segmente proporționale

în lecția aceasta o să discutăm

despre segmente proporționale dar

mai întâi vom defini Raportul a

doua segmente prin definiție Raportul

a doua segmente este raportul lungimilor

lor exprimate în aceeași unitate

de măsură avem reprezentate două

segmente ab și cd ab are 6 cm iar

CD are lungimea de 9 cm în acest

caz raportul segmentelor a b și

c d va fi Raportul lungimilor lor

6 supra 9 fracția aceasta se mai

poate simplifica cu 3 și obține

în raportul 2 supra 3 atunci când

ne referim la segmentele AB și

CD privite ca figuri geometrice

vom scrie segmentele între paranteze

drepte Dar când facem referire

la lungimea acestora din punct

de vedere algebric nu mă mai pune

și parantezele pătrate să luăm

un alt exemplu dacă avem un triunghi

m n p cu lungimile laturilor de

3 cm 4 cm și 5 cm avem următoarele

rapoarte raportul segmentelor m

n și m p va fi egal cu 3 supra

5 adică Raportul lungimilor lor

observăm că toate segmentele sunt

exprimate în aceeași unitate de

măsură raportul n p supra mp va

fi 5 supra 4 iar raportul m n supra

mp va fi 3 supra 4 în continuare

o să dăm o definiție segmentele

AB BC și CD sunt proporționale

cu segmentele MN NP și pq Dacă

lungimile lor sunt proporționale

Adică dacă avem următoarea relație

a b supra MN egal cu bc supra n

b și egal cu cd supra pq Așadar

mă îmi spune că segmentele sunt

proporționale Dacă lungimile acestora

formează un șir de rapoarte egale

Să luăm în exemplu avem următoarele

segmente ab având lungimea de 6

dm bc cu lungimea de 18 dm c d

cu lungimea de 24 dm f cu lungimea

de 9 dm f g cu lungimea de 27 dm

și gh având 36 dm să vedem dacă

aceste segmente sunt proporționale

pentru această arunc alcool la

următoarele rapoarte începem cu

Raportul a b supra ef acest raport

va fi egal cu 6 supra 9 putem să

mai simplificăm cu 3 și obținem

2 supra 3 continuăm cu următorul

la port b c supra f g BC este 18

iar fg 27 putem să simplificăm

această fracție cu 9 și obținem

2 supra 3 iar raportul CD supra

g h va fi egal cu 24 supra 36 putem

simplifica acest raport cu șase

de exemplu și obținem patru supra

6 se mai simplifică cu 2 și obținem

2 supra 3 observăm că toate aceste

rapoarte sunt egale cu 2 supra

3 așa dar aceste segmente vor fi

proporționale din aceste relații

om de duce că ab supra ef este

egal cu bc supra f g și egal cu

cd supra gh Toate aceste rapoarte

sunt 3 egal cu 2 supra 3 2 supra

3 se mai numește raportul de proporționalitate

sau Factor de proporționalitate

am arătat Așadar că segmentele

AB BC și CD sunt proporționale

cu segmentele e f f g h mă face

în continuare un exercițiu Fie

punctele e și f pe segmentul ab

astfel încât AE supra eb este egal

cu 7 supra 9 și af supra f b egal

cu 3 supra 5 Aflați valoarea raportului

af supra ab Avem două proporții

iar în aceste proporții apar patru

segmente și nu cunoaștem lungimea

acestora trebuie totuși să aflăm

valoarea raportului af supra ab

dacă ne uităm pe figură observăm

că a plus a b formează lungimea

segmentului AB să scriem acest

lucru a e plus a b este egal cu

AB și AD se notează m n tu lui

AB cu litera l mai putem observa

că af plus FB formează de asemenea

lungimea segmentului AB și în el

mai departe cu el pornind de la

proporțiile date vom obține alte

rapoarte egale folosind proporții

derivate o să mai scriu o dată

prima proporție dată în problema

AE supra eb egal cu 7 supra 9 știm

de la proporții derivate că atunci

când adunăm numitorii la numărători

sau numărătorii la numitori obținem

o nouă egalitate noi Trebuie să

aflăm valoarea raportului AE supra

eb pentru că în cerință apare segmentul

a b lăsăm numitorii dați în proporție

și adună măceș numitori la numărători

obținând astfel o nouă proporție

din această egalitate obținem a

plus a b supra a b a fi egal cu

7 plus 9 supra 9 rezultă de aici

a a plus a b este tocmai se nu

mint ul ab Deci obținem a b supra

eb egal cu 16 supra 9 exprimăm

de aici segmentul a b va rezulta

că e b este egal cu 9 ori ab supra

16 pe a blama tot cu el Deci vei

scrie în continuare 9 L supra 16

deținem această relație e b este

egal cu 9 L supra 16 mai trebuie

să îl aflăm pe a f pornind de la

a doua proporție dată în problemă

o să mai scriu odată această egalitate

a f supra f b egal cu 3 supra 5

în raportul care ni se cere apare

segmentul a f pentru al obține

pe aer din această proporție o

să adunăm numărătorii la numitori

de data aceasta astfel încât la

numărător să rămână lungimea segmentului

a e f pe care dorim să o aflăm

obținem Așadar că a f supra a plus

b egal cu 3 supra 3 plus 5 rezultă

că af supra aia plus f b este a

b egal cu 3 supra 8 de aici va

rezulta că a f este egal cu 3 ori

ab supra 8 Abel am dat cu el Deci

obținem 3 l supra 8 reținem această

relație a f este egal cu 3 n supra

8 și acum să revenim la raportul

cerut trebuie să aflăm af supra

eb și no folosi aceste două relații

pe care le am scris cu galben aif

supra eb va fi egal cu în loc de

aer scriem 3 l supra 8 iar în loc

de a b scriem 9 L supra 16 avem

aici o fracție supraetajată linia

de fracție înseamnă împărțire Deci

împărțim prima fracție la a doua

3 l supra 8 împărțit la 9 L supra

16 egal cu 3 n supra 8 ori 16 supra

9 L se simplifică 8 cu 16 rămâne

2:01 se simplifică 3 cu 9 rămâne

1 și 3 obținem l ori 2 adică 2

L supra 3 l se mai simplifică el

cu el și obținem valoarea finală

2 supra 3 raportul cerut af supra

eb va fi egal cu 2 supra 3