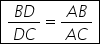Teorema bisectoarei

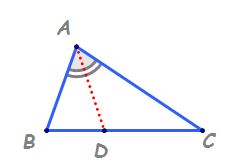
în rema bisectoarei în triunghi

bisectoarea unui unghi determină

pe latura opusă segmente proporționale

cu celelalte două laturi dacă avem

un triunghi ABC iar AD este bisectoarea

interioară a unghiului A atunci

are loc următoarea relație BD supra

DC este egal cu ab supra ac pentru

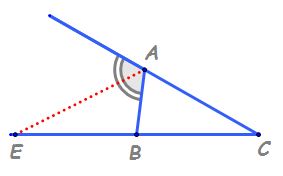
a demonstra această teoremă îmi

duce prin punctul b o paralelă

la bisectoarea ad iar această paralelă

intersectează latura AC în punctul

E putem aplica în acest caz teorema

lui Thales și obținem BD supra

de ce egal cu e a supra ac noi

trebuie să arătăm că BD supra De

ce este egal cu ab supra AC așa

dar ne mai rămâne doar Să arătăm

că ab este egal cu e a Dacă AB

e este paralelă cu ad iar ab este

secantă unghiul Eba va fi congruentă

cu unghiul b a d b nota acestei

unghiuri cu A1 și A2 Dacă aceste

două drepte sunt paralele și Considerăm

secanta e Si atunci unghiul e va

fi congruent cu unghiul A2 fiind

unghiuri corespondente A1 și a2

sunt unghiuri congruente pentru

că AD este bisectoare și atunci

va rezulta că unghiul b este congruent

cu unghiul f d și triunghiul a

b e va fi un triunghi isoscel pentru

că are două unghiuri congruente

dacă este isoscel înseamnă că latura

ab va fi congruentă cu latura a

ceea ce trebuia să și demonstrăm

unghiul Eba este congruent cu unghiul

A1 pentru că sunt unghiuri alterne

interne unghiul b i a este congruent

cu unghiul A2 fiind unghiuri corespondente

dar unghiul A1 este congruent cu

unghiul A2 pentru că AD este bisectoare

din aceste trei relații va rezulta

că unghiul Eba este congruent cu

unghiul b e a rezultă triunghiul

ABD isoscel va rezulta că AB este

egală cu a i din relația unu și

doi va rezulta următoarea relație

din 1 și 2 obținem BD supra de

ce egal cu ab supra ac am demonstrat

Așadar teorema bisectoarei iar

în continuare o să facem o aplicație

Fie abc un triunghi oarecare și

a m mediană m aparține laturii

BC bisectoarea unghiului amb intersectează

latura ab în punctul n iar bisectoarea

unghiului AMC intersectează latura

AC în punctul P Să se arate că

NP este paralelă cu bc Am scris

mai întâi ipoteza și concluzia

dacă a m este mediană înseamnă

că punctul m este situat la mijlocul

laturii BC Deci BM va fi egal cu

MC pentru a arăta că NP este paralelă

cu bc vom aplica reciproca teoremei

lui Thales ne propunem Să arătăm

că a n supra MB este egal cu ab

supra pe ce dacă reușim să arătăm

aceasta egalitate va rezulta conform

reciprocei teoremei lui tales că

NP este paralelă cu bc pentru a

demonstra aceasta egalitate vom

folosi teorema bisectoarei dacă

m n este bisectoare în triunghiul

a m b putem scrie că a n supra

n b este egal cu a m supra MB dacă

m n este bisectoare În triunghiul

amb rezultat din teorema bisectoarei

a n supra m b este egal cu a m

supra MB mp este și ea bisectoare

în triunghiul a m c și de aici

va rezulta conform teoremei bisectoarei

că a p supra p c este egal cu a

m supra m c însă m b și m c sunt

egale pentru că m este mijlocul

laturii BC m c este egal cu MB

din ipoteză și va rezulta din aceste

trei relații că avem o egalitate

între aceste rapoarte a n supra

n b este egal cu ab supra bc am

arătat Așadar că are loc această

relație va rezulta conform reciprocei

teoremei lui Thales n p este paralelă

cu bc