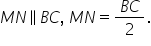Linia mijlocie în triunghi (teorie)
Tag-uri
Partajeaza in Google Classroom
Transcript
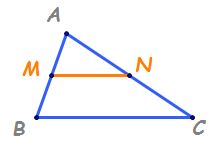
linia mijlocie in triunghi segmentul
care unește mijloacele a doua laturi
ale unui triunghi se numește linie
mijlocie în triunghiul ABC am notat
cu M mijlocul laturii a b și n
mijlocul laturii ac spune că mn
este linie mijlocie în triunghiul
ABC dacă fix în mijlocul segmentului
BC și notăm cu litera P atunci
observăm că în triunghiul ABC putem
construi trei linii mijlocii acestea
sunt MN MP și NP în continuare
o să dăm o proprietate al liniei
mijlocii sub forma unei teoreme
linia mijlocie determinată de două
laturi este paralelă cu cea de
a treia latură a triunghiului și
are lungimea egală cu jumătate
din lungimea acesteia om Demonstrați
teorema Se știe că mn este linie
mijlocie și trebuie să arătăm că
mn este paralelă cu bc și că lungimea
segmentului mn este jumătate din
lungimea segmentului BC pentru
a face demonstrația acestei teoreme
avem nevoie de o construcție ajutătoare
100 ducem prin punctul c o paralelă
la latura ab fie c p paralelă cu
AB pentru a demonstra că mn este
paralelă cu bc ne propunem Să arătăm
că patrulaterul m b c p este paralelogram
iar pentru aceasta va trebui să
arătăm că acest patrulater are
două laturi opuse paralele și congruente
Cum arăta că pe c și m b sunt paralele
și congruente relația de paralelism
dintre acestea rezultă din construcția
făcută Deci mai trebuie doar să
arătăm că pe ce este congruent
cu MB pentru aceasta vom arăta
că Triunghiurile a m n și c p n
sunt congruente având în vedere
că ab este paralelă cu bc iar AC
este secantă înseamnă că unghiul
m a n este congruent cu unghiul
b c n fiind unghiuri alterne interne
se știe din ipoteză că a n este
congruent cu nc pentru că n este
mijlocul laturii ac și mai observăm
că unghiul a n m este congruent
cu unghiul c n p fiind unghiuri
opuse la vârf unghiul m a n este
congruent cu unghiul p c n endo
unghiuri alterne interne segmentul
a n este congruent cu segmentul
n c din ipoteză și unghiul a n
m este congruent cu unghiul c n
p fiind unghiuri opuse la vârf
din aceste trei relații rezultă
conform cazului de congruență unghii
latură unghi că triunghiul a m
n este congruent cu triunghiul
c p n notam deocamdată această
relație cu unu ne va folosi ulterior
din congruența acestor triunghiuri
rezultă că segmentul BC este congruent
cu a m dar a m este congruent cu
MB pentru că punctul m este mijlocul
laturii ab a m fiind congruent
cu MB Ba rezultat din cele două
relații pe ce este congruent cu
MB am arătat Așadar că patrulaterul
m b c p are două laturi opuse paralele
și congruente și atunci pa rezulta
ca acesta este paralelogram din
relațiile 2 și 3 rezultă că patrulaterul
m b c p este paralelogram înseamnă
că și celelalte două laturi mp
și BC boși paralele și congruente
rezultă m p paralelă cu b c și
atunci implicit m n a fi paralelă
cu b c pentru că punctele m n p
sunt coliniare am demonstrat Așadar
punctul A al teoremei mai trebuie
să arătăm că mn este jumătate din
bc Dacă m b c p este paralelogram
rezultat că laturile opuse sunt
și congruente mp va fi congruent
cu BC asta din Relația de congruență
a acestor două triunghiuri mai
rezultă faptul că segmentul mn
este congruent cu NP înseamnă că
punctul n este mijlocul laturii
mp Deci m n va fi jumătate din
mp însă mp fiind congruent cu BC
la rezultat că mn este jumătate
din BC astfel am demonstrat și
punctul B al teoremei din relația
unu adică din congruență a celor
două triunghiuri rezultat că segmentul
MN este congruent cu mp și va rezulta
din această relație că mn este
jumătate din mp mp fiind congruent
cu BC mai rezultat că mn este jumătate
din bc și am demonstrat și punctul
B alte ori ma este foarte important
să rețineți că linia mijlocie a
unui triunghi este paralelă cu
cea de a treia latură a triunghiului
și are lungimea egală cu jumătate
din lungimea acestuia în continuare
o să mai ai enunță Matteo rama
Dacă M este mijlocul laturii ab
a triunghiului ABC și MN este paralelă
cu bc atunci n este mijlocul laturii
ac putem folosi această teoremă
atunci când trebuie să arătăm că
un segment este linie mijlocie
a unui triunghi Dacă punctul m
este mijlocul laturii ab iar mn
este paralelă cu bc atunci va rezulta
implicit că și punctul n este mijlocul
laturii ac Deci MN va fi linie
mijlocie a triunghiului
Linia mijlocie în triunghi- definiție și proprietățiAscunde teorie X
Navigare în lectii
Cumpara abonament
