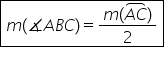Unghi înscris în cerc (teorie)

să privim puțin aceste figuri geometrice

și să vedem ce asemănări și deosebiri

există între ele în primul caz

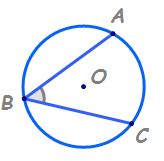
observăm că vârful unghiului este

situat pe cerc în al doilea caz

vârful unghiului este situat în

exteriorul cercului în a treia

figură vârful unghiului este situat

pe cerc iar în a patra figură vârful

unghiului este situat în interiorul

cercului putem astea să remarcăm

că figurile 1 și 3 sunt asemănătoare

prin faptul că cele două unghiuri

au vârfurile situate pe cerc iar

laturile lor sunt coardă ale cercului

astfel de unghiuri se vor numi

unghiuri înscrise în cerc o să

dăm și definiția se numește unghi

înscris în cerc unghiul cu vârful

pe cerc și care are ca laturi de

o coardă ale cercului astfel putem

spune că unghiurile b a c și m

n p sunt unghiuri înscrise în cerc

arcele mici b c și m p se numesc

a c cuprinse între laturile unghiurilor

înscrise în continuare o să vedem

ce legătură există între măsura

unghiului înscris în cerc și măsura

arcului cuprins între laturile

sale mai întâi o să vedem o teoremă

care ne va fi utilă în demonstrația

următoarelor teoreme dacă a și

b sunt două puncte distincte ale

unui cerc și m este un punct care

aparține arcului ab atunci măsura

arcului AB se compune din măsura

arcului a m plus măsura arcului

m b și în continuare o să dăm o

teoremă referitoare la Măsura unui

unghi înscris în cerc teorema numărul

2 Măsura unui unghi înscris în

cerc este jumătate din măsura arcului

cuprins între laturile sale am

demonstrat ceastă teoremă și o

să vedem că există trei cazuri

posibile în funcție de poziție

a punctului o față de unghiul bac

în primul caz considerăm că punctul

O aparține unei laturi a unghiului

Deci coarda AC este chiar diametrul

cercului în primul caz le propunem

Să arătăm că măsura unghiului BAC

este jumătate din măsura arcului

b c pentru aceasta o să unesc punctele

B și o astăzi sau format un triunghi

triunghiul AOB Acesta este un triunghi

isoscel deoarece laturile a o și

b o sunt congruente acesteia fiind

raze ale cercului mare triunghiul

AOB are unghiurile de la bază congruente

și mai putem observa că unghiul

b o c este un unghi exterior acestui

triunghi și vom aplica teorema

referitoare la Măsura unghiului

exterior unui triunghi mai întâi

să scriem că triunghiul AOB este

un triunghi isoscel pentru că a

o este egal cu b o și egal cu raza

cercului prin urmare măsura unghiului

a b o va fi egală cu măsura unghiului

b a o pentru că triunghiul isoscel

are unghiurile alăturate bazei

congruente unghiul b o c este un

unghi exterior triunghiului aob

și vom aplica teorema referitoare

la Măsura unui unghi exterior unui

triunghi aceasta este egală cu

suma unghiurilor triunghiului neadiacente

cu el Deci măsura unghiului b o

c a fi egală cu măsura unghiului

a b o plus măsura unghiului b a

o însă cu cele două măsuri sunt

egale pentru că unghiurile sunt

congruente și atunci Putem să scriem

că măsura unghiului b o c va fi

egală cu 2 ori măsura unghiului

b a o dar trebuie să arătăm că

măsura unghiului BAC este jumătate

din măsura arcului b c din această

relație exprima măsura unghiului

Ba o împărțim calitatea la 2:00

și astfel obținem că măsura unghiului

b a o va fi egală cu măsura unghiului

b o c supra 2 Dar unghiul de o

c este unghiul la centru iar măsura

unui unghi la centru este egală

cu măsura arcului cuprins între

laturile sale Deci măsura unghiului

BOC va fi egală cu măsura arcului

b c supra 2 am arătat astfel că

măsura unghiului b a o este jumătate

din măsura arcului b c prin urmare

și măsura unghiului b a c adică

măsura unghiului înscris în cerc

este jumătate din măsura arcului

cuprins între laturile sale am

arătat că teorema este adevărată

în cazul în care punctul O aparține

uneia dintre laturile unghiului

continuăm cu al doilea caz azul

2 ne propunem Să arătăm că măsura

unghiului BAC este jumătate din

măsura arcului bc Dacă Punctul

o este situat în interiorul unghiului

putem să ducem O dreaptă care să

treacă prin punctele a și o această

dreaptă intersectează cercul în

punctul d cu alte cuvinte am construit

diametrul ad atunci măsura unghiului

BAC este suma măsurilor unghiurilor

b a d și d a c dar măsura unghiului

b a d este jumătate din măsura

arcului BD am văzut acest lucru

la primul caz cel pe care îl am

demonstrat mai devreme în care

punctul O este situat pe una dintre

laturile unghiului deci putem să

scriem egal în continuare cu măsura

arcului b d supra 2 iar măsura

unghiului dac va fi jumătate din

măsura arcului d c observăm astfel

că al doilea caz de fapt se reduce

la primul caz Măsura arcului b

d plus măsura arcului d c este

egală cu măsura arcului b c supra

2 am demonstrat astfel că măsura

unghiului înscris b AC este jumătate

din măsura arcului cuprins între

laturile sale și mai există o variantă

posibilă cea în care punctul O

este situat în exteriorul unghiului

BAC acesta va fi cazul 3 avem unghiul

înscris în cerc bac și ne propunem

să demonstrăm că măsura acestui

unghi este jumătate din măsura

arcului bc cazul 3 Dacă Punctul

o este situat în exteriorul unghiului

putem să construim și de această

dată diametrul ad și vom exprima

măsura unghiului BAC ca fiind diferența

dintre unghiurile b a d și ce Ade

măsura unghiului BAC va fi egală

cu măsura unghiului b a d minus

măsura unghiului c a d dar măsura

unghiului b a d este jumătate din

măsura arcului BD observăm că și

cazul trei se reduce la primul

caz cel în care punctul O este

situat pe una dintre laturile unghiului

egal cu măsura arcului BD supra

2 minus măsura unghiului c a d

va fi și aceasta jumătate din măsura

arcului cuprins între laturile

sale mai exact jumătate din măsura

arcului CD însă Măsura arcului

BD minus măsura arcului CD este

egală cu măsura arcului bc egal

cu măsura arcului b c supra 2 această

teoremă are și niște consecințe

importante O primă consecință unghiul

înscris în semicerc este un unghi

drept dacă BC este un diametru

în acest cerc atunci arcul bc se

numește semicerc iar unghiul bac

va fi un unghi înscris în semicerc

dacă un cerc întreg are măsura

de 360 de grade înseamnă că semicercul

b c are măsura egală cu 180 de

grade iar unghiul înscris în semicerc

va fi jumătate din măsura arcului

bc adică 180 de grade supra 2 și

obținem 90 și o ador consecință

importantă toate Unghiurile înscrise

în același arc sunt congruente

avem trei unghiuri cu vârfurile

în punctele m n și p măsurile celor

trei unghiuri vor fi toate egale

cu jumătate din măsura arcului

AB prin urmare cele trei unghiuri

MN și PM vor fi unghiuri congruente

Acum putem să extindem puțin această

noțiune de unghi înscris în cerc

și în continuare o să vedem o teoremă

referitoare la un alt tip de unghi

cel care are una din laturi secantă

la cerc și cealaltă tangentă la

cerc astfel Măsura unui unghi cu

vârful pe cerc care are una dintre

laturi secantă iar cealaltă tangentă

la cerc este jumătate din măsura

arcului cuprins între laturile

sale observăm astfel că teorema

rămâne valabilă și în acest caz

și atunci Putem să scriem că măsura

unghiului BAC va fi egală cu măsura

arcului ba supra 2 în continuare

o să definim triunghiul înscris

în cerc Un triunghi este înscris

în triunghi cerc dacă vârfurile

sale aparțin cercului în această

figură observăm că vârfurile triunghiului

ABC sunt puncte situate pe cerc

iar în acest caz triunghiul ABC

se numește triunghi înscris în

cerc iar cercul se va numit cerc

circumscris triunghiului ABC