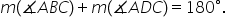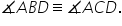Patrulater înscris în cerc; patrulater inscriptibil

în această lecție o să vorbim despre

patrulater înscris în cerc și patrulater

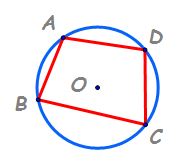
inscriptibil un patrulater se numește

înscris întru un cerc dacă vârfurile

sale aparțin cercului observăm

că patrulaterul abcd are vârfurile

situate pe același cerc în acest

caz patrulaterul se numește înscris

în cerc Nu toate patrulaterele

sunt înscrise în cerc de exemplu

patrulaterul mnpq nu are vârfurile

situate pe același cerc și în acest

caz El nu este înscris în cerc

o să vedem în continuare câteva

proprietăți ale patrulaterelor

înscrise în cerc sub forma unor

teoreme prima teoremă un patrulater

înscris în cerc are Unghiurile

opuse suplementare Demonstrați

teoremă trebuie să arătăm că măsura

unghiului a d c plus măsura unghiului

abc este egală cu 180 de grade

și Analog se va demonstra că și

celelalte unghiuri opuse a și c

sunt suplementare demonstrație

vom calcula măsura unghiului adc

plus măsura unghiului abc unghiul

abc este un unghi înscris în cerc

iar măsura unui unghi înscris în

cerc este jumătate din măsura arcului

cuprins între laturile sale astfel

măsura unghiului adc va fi egală

cu jumătate din măsura arcului

abc egal cu măsura arcului abc

supra 2 plus măsura unghiului abc

va fi egală cu jumătate din măsura

arcului cuprins între laturile

acestui unghi adică jumătate din

măsura arcului a d c trebuie să

adunăm două fracții cu același

numitor putem să adunăm numărătorii

observăm că măsura arcului a b

c plus măsura arcului a d c va

fi egală cu 360 de grade pentru

că ele formează un cerc și atunci

Putem să scriem egal cu 360 de

grade supra 2 egal cu 180 de grade

am arătat astfel că unghiurile

b și d sunt suplementare pentru

că suma măsurilor acestora este

de 180 de grade în mod asemănător

se poate arăta că unghiurile a

și c sunt suplementare și o altă

proprietate a patrulaterelor înscrise

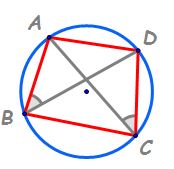
teorema numărul 2 Dacă un patrulater

este înscris în cerc atunci diagonalele

sale formează cu două laturi opuse

unghiuri congruente avem patrulaterul

înscris a b c d m Demonstrați că

unghiul bac este congruent cu unghiul

bdc în mod Analog se poate demonstra

că și celelalte unghiuri formate

de diagonale cu laturile opuse

sunt congruente demonstrație vom

calcula mai întâi măsura unghiului

cdb unghiul cdb este un unghi înscris

în cerc Așadar măsura acestui unghi

va fi jumătate din măsura arcului

cuprins între laturile sale este

vorba de Arcul bc egal cu măsura

arcului b c supra 2 acum calculăm

măsura unghiului BAC și acesta

este un unghi înscris în cerc iar

măsura lui va fi jumătate din măsura

arcului cuprins între laturile

sale observăm că este vorba despre

același arc bc egal cu măsura arcului

BC supra 2 observăm astfel că măsurile

celor două unghiuri sunt egale

prin urmare unghiurile congruente

unghiul cdb va fi congruent cu

unghiul bac în mod Analog se demonstrează

și congruență a celorlalte unghiuri

determinate de diagonale cu laturile

opuse în continuare o să dăm niște

definiții patru puncte se numesc

conciclice dacă există un cerc

care să le conțină pe toate de

exemplu punctele mnpq sunt puncte

conciclice Deoarece ele aparțin

aceluiași cerc un patrulater se

numește inscriptibil dacă vârfurile

sale sunt puncte conciclice altfel

spus un patrulater este inscriptibil

dacă poate fi înscris pentru un

cerc și în continuare o să vedem

câteva teoreme referitoare la patrulaterele

inscriptibile prima teoremă un

patrulater este inscriptibil dacă

și numai dacă unghiurile opuse

sunt suplementare o a doua proprietate

un patrulater este inscriptibil

dacă și numai dacă Orice unghi

format de o diagonală cu o latură

este congruent cu unghiul format

de cealaltă diagonala cu latura

opusă primei Ia și un patrulater

este inscriptibil dacă și numai

dacă mediatoarele laturilor sale

sunt concurente iar punctul lor

de intersecție reprezintă centrul

cercului vă reamintesc că Mediatoarea

unui segment este perpendiculara

ridicată din mijlocul segmentului

în patrulaterul a b c d am construit

cu galben mediatoarele laturilor

observăm că acestea se intersectează

în punctul o Care este de fapt

centrul cercului având la dispoziție

aceste teoreme de caracterizare

a patrulaterelor inscriptibile

putem să tragem niște concluzii

pătratul și dreptunghiul sunt patrulatere

inscriptibile însă rombul și paralelogramul

nu sunt patrulatere inscriptibile

în continuare o să facem o aplicație

vom rezolva următoarea problemă

pe un cerc se consideră punctele

a b c și d astfel încât măsura

arcului AB este egală cu 140 de

grade Măsura arcului BC este egală

cu 60 de grade și măsura arcului

CD este egală cu 120 de grade calculați

măsurile arcelor a d b c d a d

c d AB și abc măsurile unghiurilor

patrulaterului a b c d și măsurile

unghiurilor formate de diagonale

cu laturile patrulaterului demonstrație

măsura arcului AB este egală cu

140 de grade Măsura arcului BC

este 60 de grade Măsura arcului

CD este 120 de grade trebuie să

calculăm mai întâi Măsura arcului

a d știm că un cerc are 360 de

grade pentru a calcula Măsura arcului

ad din cele 360 de grade o să scădem

măsurile arcelor ab bc și CD punctul

a măsura arcului a d este egală

cu 360 de grade minus măsura arcului

AB plus măsura arcului bc plus

măsura arcului de ce egal cu 360

de grade minus 140 de grade plus

60 de grade plus 120 de grade egal

140 plus 60 este 200 plus 120 320

iar 360 minus 320 este egal cu

40 de grade măsura arcului a d

este egală cu 40 de grade acum

trebuie să calculăm Măsura arcului

b c d aceasta se obține adunând

măsurile arcelor BC și CD Măsura

arcului b c d este egală cu măsura

arcului bc plus măsura arcului

CD egal cu 60 de grade plus 120

de grade egal 180 de grade Măsura

arcului a d c este formată din

măsura arcului ad plus măsura arcului

d c dar cu 40 de grade plus 120

de grade egal cu 160 de grade continuăm

cu măsura arcului D AB aceasta

este egală cu măsura arcului Da

toți măsura arcului AB Măsura arcului

D AB este egală cu măsura arcului

d a plus măsura arcului AB egal

cu 40 de grade plus 140 de grade

și egal cu 180 de grade și mai

trebuie să calculăm Măsura arcului

a b c aceasta este egală cu măsura

arcului AB plus măsura arcului

bc egal cu 140 de grade plus 60

de grade egal cu 200 de grade continuăm

cu punctul B trebuie să calculăm

măsurile unghiurilor patrulaterului

a b c d să începem de exemplu cu

măsura unghiului A unghiul A este

un unghi înscris în cerc iar măsura

unghiului a este jumătate din măsura

arcului cuprins între laturile

sale Putem să scriem că măsura

unghiului a este egală cu măsura

arcului b c d supra 2 Am calculat

deja Măsura arcului b c d aceasta

este 180 de grade 180 de grade

supra 2 egal cu 90 de grade având

în vedere că a b c d este un patrulater

înscris în cerc înseamnă că unghiurile

opuse sunt suplementare și atunci

putem calcula măsura unghiului

c scăzând din 180 de grade măsura

unghiului A sau putem calcula măsura

unghiului c făcând referire la

Măsura arcului cuprins între laturile

sale oricare dintre cele două variante

Este corectă o să folosesc proprietatea

patrulaterelor înscrise care ne

spune că unghiurile opuse sunt

suplementare astfel măsura unghiului

c va fi egală cu 180 de grade minus

măsura unghiului a egal cu 180

de grade minus 90 și egal cu 90

de grade pentru că a b c d este

un patrulater înscris încerc mai

trebuie să calculăm măsurile unghiurilor

b și d calculăm măsura unghiului

B aceasta va fi egală cu jumătate

din măsura arcului a d c egal cu

măsura arcului a d c supra 2 Am

calculat deja Măsura arcului a

d c aceasta este 160 de grade iar

160 supra 2 este egal cu 80 astfel

măsura unghiului b este egală cu

80 de grade pentru a calcula măsura

unghiului d folosind faptul că

unghiurile b și d sunt unghiuri

opuse suplementare măsura unghiului

D este egală cu 180 de grade minus

măsura unghiului B egal cu 180

de grade minus 80 de grade și egal

cu 100 de grade Am calculat cele

patru măsuri ale unghiurilor patrulaterului

a b c d în continuare trebuie să

calculăm la punctul c unghiurile

formate de diagonale cu laturile

patrulaterului ducem și diagonalele

AC și BD o să șterg cele scrise

până acum ca să am spațiu pentru

rezolvarea punctului C o să calculăm

mai întâi măsura unghiului BAC

Acesta este un unghi înscris în

cerc iar măsura sa este egală cu

jumătate din măsura arcului bc

măsura unghiului BAC este egală

cu măsura arcului bc supra 2 egal

cu 60 de grade supra 2 și egal

cu 30 de grade Unghiul BAC este

congruent cu unghiul bdc am văzut

această proprietate în teorema

numărului 2 pentru că cele două

unghiuri cuprind între laturile

lor același arc BC și atunci Putem

să scriem că măsura unghiului bdc

este egală cu măsura unghiului

BAC și egală cu 30 de grade conform

teoremei numărul 2 calculăm în

continuare măsura unghiului dac

aceasta va fi egală cu măsura unghiului

d b c pentru că cele două unghiuri

cuprind între laturile lor același

arc de ce măsura unghiului dac

este egală cu măsura unghiului

dbc și egală cu jumătate din măsura

arcului de ce egal cu 120 de grade

supra 2 și egal cu 60 m continuat

cu măsura unghiului ABD aceasta

va fi egală cu măsura unghiului

acd pentru că cele două unghiuri

cuprind între laturile lor același

arc ad măsura unghiului ABD este

egală cu măsura unghiului acd și

egală cu jumătate din măsura arcului

a d egal cu 40 de grade supra 2

și egal cu 20 de grade și au mai

rămas unghiurile ACB și adb care

vor fi și acesteia congruente măsura

unghiului ACB va fi egală cu măsura

unghiului adb și gală cu jumătate

din măsura arcului AB arcul ab

are 140 de grade 140 împărțit la

2 este egal cu 70 de grade am aflat

astfel măsurile unghiurilor determinate

de diagonale cu laturile patrulaterului

ABCD