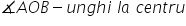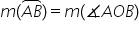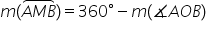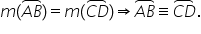Unghi la centru
Tag-uri
Partajeaza in Google Classroom
Transcript
în această lecție o să discutăm
despre unghi la centru un unghi
cu vârful în centrul unui cerc
se numește unghi la centru observăm
că Unghiul aob are vârful în punctul
o Care este centrul cercului în
acest caz un spune că Unghiul aob
este unghi la centru așe exemplu
ar fi Unghiul aob măsura unui arc
mic de cerc este egală cu măsura
unghiului la centru corespunzător
în această figură arcul mic ab
va avea măsura egală cu măsura
unghiului la centru aob măsura
arcului AB se notează astfel ea
a fi egală cu măsura unghiului
la centru a o b iar prin definiție
măsura unui arc mare de cerc este
egală cu diferența dintre 360 de
grade și măsura unghiului la centru
corespunzător arcului mic pentru
a înota arcul mare a mai fixat
un punct M și astfel Măsura arcului
a m b va fi egală cu 360 de grade
minus măsura unghiului la centru
corespunzător arcului mic adică
măsura unghiului aob În consecință
putem de duce măsura unui semicerc
măsura unui semicerc este de 180
de grade pentru că Unghiul aob
este un unghi alungit iar măsura
unui cerc întreg este de 360 de
grade dacă AB este diametru atunci
va rezulta că măsura semicercului
ab va fi egală cu 180 de grade
iar măsura unui cerc întreg va
fi de două ori mai mare decât măsura
unui semicerc adică 2 ori 180 și
obținem 360 de grade și o ultimă
definiția două sau mai multe arce
ale aceluiași cerc sau din cercuri
congruente se numesc arce congruente
dacă au aceeași măsură mai întâi
să vedem ce sunt cercurile congruente
două cercuri se numesc congruențe
dacă au aceeași rază iar două arce
care fac parte fie din același
cerc fie din cercuri congruente
se vor numi congruente dacă au
aceeași măsură astfel Dacă măsura
arcului AB este egală cu măsura
arcului CD cu alte cuvinte cele
două unghiuri a o b și c o d sunt
congruente atunci ma rezulta ca
aceste două arce sunt congruente
și vom scrie în felul următor arcul
AB este congruent cu arcul CD o
să facem un continuare un exemplu
avem un unghi la centru AOB cu
măsura de 80 de grade atunci măsura
arcului AB va fi egală cu măsura
unghiului la centru aob egal cu
80 de grade iar măsura arcului
mare adb va fi egală cu 360 de
grade minus măsura unghiului la
centru corespunzător arcului mic
egal cu 360 de grade minus 80 de
grade egal cu 280 de grade
Unghi la centru, măsura unui arc de cercAscunde teorie X
.JPG)
Navigare în lectii
Cumpara abonament
