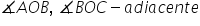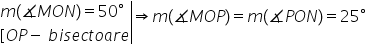Unghiuri adiacente. Bisectoarea unui unghi. Teorie
Tag-uri
Partajeaza in Google Classroom
Transcript
unghiuri adiacente bisectoarea
unui unghi avem următoarea definiție
două unghiuri care au măsurile
egale se numesc unghiuri congruente
în această figură observăm că măsura
unghiului abc este de 50 de grade
la fel și măsura unghiului m n
p este tot de 50 de grade și atunci
vom spune că aceste două unghiuri
sunt congruente Acest lucru se
va scrie astfel unghiul abc este
congruent cu unghiul m n p dacă
ne referim la măsurile lor îmi
scrie că acestea sunt egale măsura
unghiului abc este egală cu măsura
unghiului r&b în continuare vom
da definiția unghiurilor adiacente
două unghiuri care au vârful comun
și o latură comună situată în interiorul
unghiului format de celelalte două
laturi se numesc unghiuri adiacente
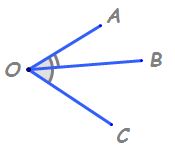
observăm că unghiurile a o m și
m o b au vârful comun acesta este
punctul o și au o latură comună
aceasta este semidreapta om care
este situată în interiorul unghiului
format de celelalte două laturi
8 spune ca aceste două unghiuri
sunt unghiuri adiacente Deci unghiul
a o m și unghiul m o b sunt unghiuri
adiacente urmează să dăm definiția
bisectoarei unui unghi bisectoarea
unui unghi este semidreapta cu
originea în vârful unghiului situată
în interiorul acestuia care formează
cu laturile unghiului inițial două
unghiuri congruente avem Unghiul
aob și am construit în interiorul
acestuia semidreapta om care împarte
unghiul în două unghiuri congruente
spune că OM este bisectoarea unghiului
AOB Așadar dacă avem un unghi aob
și OM este bisectoarea acestuia
se vor forma două unghiuri congruente
unghiul aom va fie congruent cu
unghiul n o b să vedem cum putem
să construim bisectoarea unui unghi
avem unghiul c o d sinonim să construim
bisectoarea acestuia mai întâi
va trebui să aflăm măsura unghiului
c o d apoi această măsură avem
împărțit la 2 astfel încât să putem
construi bisectoarea unghiului
respectiv pentru a afla măsura
unghiului c o d folosind raportorul
observăm că acesta are măsura de
60 de grade și atunci vom duce
semidreapta care va forma bisectoarea
unghiului în dreptul măsurii de
30 de grade îndepărtăm raportorul
și acum unim punctul O cu punctul
respectiv notis această semidreaptă
cu om și să format aici două unghiuri
fiecare cu măsura de 30 de grade
Așadar avem dată măsura unghiului
c o d de 60 de grade am construit
bisectoarea OM și sau Formează
două unghiuri care au măsurile
egale măsura unghiului c o m este
egală cu măsura unghiului m o d
și egală cu 30 de grade basmul
în care avem un unghi drept și
construim bisectoarea acestuia
ia vapor ma cu laturile unghiului
inițial două unghiuri congruente
având fiecare măsura de 45 de grade
Dacă măsura unghiului m o n este
de 90 de grade și construim bisectoarea
o p A rezultat că măsura unghiului
m o p este egală cu măsura unghiului
P o n ce e egală cu 45 de grade
iar cazul în care avem un unghi
obtuz Să presupunem că avem unghiul
p q r cu măsura de 140 de grade
și am construit e bisectoarea q
s se vor forma două unghiuri congruente
scrie că măsura unghiului p q s
este egală cu măsura unghiului
s q r și dar mai departe cu 140
de grade împărțit la 2 egal cu
70 de grade aceste două unghiuri
vor avea fiecare măsura de 70 de
grade
Unghiuri congruente. Bisectoarea unui unghiAscunde teorie X
Navigare în lectii
Cumpara abonament
