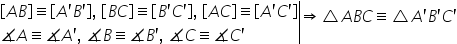Cazurile de congruenţă ale triunghiurilor oarecare

în această lecție am discutat despre

congruența triunghiurilor oarecare

ne reamintim că două segmente se

numesc congruențe dacă au aceeași

lungime Dacă lungimea segmentului

AB este egală cu lungimea segmentului

MN acest lucru implică congruență

a celor două segmente a b va fi

congruentă cu segmentul m n iar

dacă avem două unghiuri astfel

încât măsura unghiului a să fie

egală cu măsura unghiului m de

aici ma rezultă că unghiul a va

fie congruent cu unghiul m să primim

în continuare următoarele două

triunghiuri avem triunghiul abc

și triunghiul a prim b prim c prim

dacă ne uităm la lungimile laturilor

acestor triunghiuri observăm că

Segmentul ab este congruent cu

segmentul a prim b prim segmentul

BC este congruent cu b prim c prim

și ac este congruent cu a prim

c prim diferitor la unghiuri putem

observa o relație de congruență

între unghiul A și unghiul a prim

Între unghiul b și b prim și de

asemenea unghiul c este congruent

cu unghiul c prim îmi spune că

cele două triunghiuri se numesc

triunghiuri congruente o să dăm

și definiția Fiind date două triunghiuri

abc și a prim b prim c prim spunem

că acestea sunt congruente dacă

sunt îndeplinite următoarele relații

segmentul a b este congruent cu

segmentul a prim b prim segmentul

BC este congruent cu b prim c prim

și segmentul C A este congruent

cu c prim a prim și avem de asemenea

o relație de congruență între unghiurile

acestori triunghiuri unghiul A

este congruent cu unghiul a prim

unghiul b cu unghiul b prim și

unghiul c congruent cu unghiul

surprins scrie că triunghiul ABC

este congruent cu triunghiul a

prim b prim c prim cu alte cuvinte

Două triunghiuri sunt congruente

dacă ele coincid prin suprapunere

laturile și unghiurile acestor

două triunghiuri între care există

o corespondență determinată de

congruență a celor două triunghiuri

se numesc elemente omoloaga exemplu

Stai că mentele a b și a prim b

prim se numesc elemente omoloage

iar unghiul c cu unghiul c prim

vor fi de asemenea elemente omule

ace în lecția trecută am văzut

că putem construi triunghiuri Cunoscând

doar trei elemente înseamnă că

dacă vom construi două triunghiuri

având câte trei elemente congruente

ele boschi congruentei nu e necesar

demonstrăm toate cele 6 congruențe

între elementele celor două triunghiuri

Așadar putem deduce următoarele

cazuri de congruență ale triunghiurilor

oarecare primul caz de congruență

este latura unghi latura două triunghiuri

care au câte două laturi congruente

și unghiurile determinate de acestea

respectiv congruente sunt congruente

dacă ne uităm la cele două triunghiuri

a b c și m n p putem observa următoarele

relații între elementele acestora

segmentul a b este congruent cu

segmentul m n unghiul b este congruent

cu unghiul n și latura bc este

congruentă cu latura NP din aceste

trei relații va rezulta conform

acestui caz latura unghi latura

că triunghiul abc va fi congruent

cu triunghiul MNP următorul caz

de congruență cazul unghi latura

unghi două triunghiuri care au

câte o latură și unghiurile alăturate

ei respectiv congruente sunt congruente

în triunghiul a p q r și s t v

observăm că latura q este congruentă

cu TV și unghiurile alăturate acestor

două segmente sunt unghiuri congruente

unghiul q este congruent cu unghiul

b segmentul q r este congruent

cu segmentul TV și unghiul R este

congruent cu unghiul b din aceste

trei relații rezultă cu acolo cazului

unghi latura unghi că triunghiul

p q r este congruent cu triunghiul

s TV și următorul caz de congruență

cazul latura latura latura două

triunghiuri care au toate laturile

respectiv congruente sunt congruente

în aceste două triunghiuri putem

observa următoarea relație de congruență

segmentul a o este congruent cu

segmentul MN apoi segmentul OB

este congruent cu mp și latura

ab este congruentă cu latura mp

din aceste trei relații rezultă

conform cazului latura latura latura

că triunghiul a o b va fi congruent

cu triunghiul m n p ar mai exista

un caz de congruență latura unghi

unghi dar acela se reduce la cazul

unghii latură unghi Deci principalele

cazuri de congruență rămân acestea

trei în continuare o să facem o

aplicație Fie triunghiul ABC congruent

cu triunghiul m o n conform figurii

de mai jos Aflați lungimea segmentului

BC și măsura unghiului m o n observăm

că lungimea segmentului AB este

de 5 cm și la fel lungimea segmentului

m o este tot de 5 cm înseamnă că

Segmentul ab este congruent cu

segmentul m o apoi observăm că

segmentul AC este congruent cu

segmentul MN deoarece amândouă

au lungimea de 6 cm dat fiind faptul

că triunghiurile sunt congruente

acest lucru implică și congruența

celei de a treia laturi și anume

bc va fi congruentă cu latura o

n de aici putem trage concluzia

că bc va avea lungimea de 8 cm

Să redactăm cele spuse până acum

având în vedere că triunghiul ABC

este congruent cu triunghiul m

o n de aici ma rezulta pe latura

b c este congruentă cu latura o

n pentru că congruență a triunghiurilor

implică congruența elementelor

omoloage de unde rezultă că bc

va fi egal cu o n și egal cu 8

cm mai trebuie să aflăm măsura

unghiului m o n acest unghi va

fi congruent cu unghiul b din triunghiul

abc în să observăm că nu cunoaște

Nici măsura unghiului B va trebui

să aflăm măsura unghiului B după

care vom putea deduceți și măsura

unghiului o În triunghiul ABC se

știe că suma măsurilor unghiurilor

este de 180 de grade voi scrie

că măsura unghiului a plus măsura

unghiului B îți măsura unghiului

c este egală cu 180 de grade această

proprietate este valabilă pentru

orice triunghi măsura unghiului

a este de 84 de grade plus măsura

unghiului B iar măsura unghiului

c este de 42 de grade egal mai

departe cu 180 de grade putem să

adunăm 84 cu 42 pentru că adunarea

este asociativă obținem 100 26

de grade plus măsura unghiului

B egal cu 180 de grade scădem cele

126 de grade din fiecare membru

al legalității și obținem că măsura

unghiului B va fi egală cu 180

de grade minus 126 de grade adică

măsura unghiului B va fi egală

cu 54 de grade revenind la desen

Putem afirma că unghiul b este

congruent cu unghiul o și atunci

măsura unghiului o va fi de 54

de grade având în vedere că triunghiul

ABC este congruent cu triunghiul

m o n a rezultat că unghiul b este

congruent cu unghiul o Așadar măsura

unghiului o ma fie egală cu 54

de grade în concluzie măsura unghiului

m o n este egală cu 54 de grade