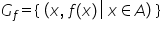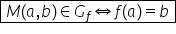Graficul unei funcții

Până acum am întâlnit funcții definite

pe mulțimi finite de exemplu f

definită pe mulțimea formată din

elementele 0 1 2 cu valori întru

altă mulțime o notăm cu C mare

de la codomeniu însă domeniul de

definiție al unei funcții poate

fi și o mulțime infinită dar în

această secvență vom discuta despre

graficul unei funcții când funcția

a definită pe o mulțime finită

și întru altă secvență o să discutăm

și despre alte situații și nici

se dă funcția f definită pe această

mulțime avem elementele 1 3 6 cu

valori în această mulțime f de

x egal x minus doi și vrem să vedem

care este graficul funcției f pentru

început vrem să determinăm valorile

funcției în aceste puncte Deci

mulțimea de Valori a funcției f

și vom face un tabel de valori

pentru că e mult mai ușor de urmărit

pe prima linie vom trece valorile

lui x iar pe a doua linie valorile

funcției în numerele respective

adică avem aici f d x x poate fi

1 3 și 6 aici si vom avea Păi dacă

x este unul sub el vom avea fd1

aici vom avea f de 3 și aici am

avea f de 6 și să calculăm Cât

este f de 1 Păi f de 1 ne dă 1

minus 2 să notăm adică minus 1

și nu o să șterg aici ro să lase

fd1 să scriem de de sub valoarea

de sinus de 3pi e f de 3 ne dă

3 minus 2 3 minus 2 Adică 1 unde

îl trecem aici fdt haine de un

e f d 6 este 4 pardon este 6 minus

doi deja mă gândeam la rezultat

adică 4:00 venim și trecem aici

4:00 e bine în acest moment Noi

am găsit niște perechi de numere

și aceste perechi Realizează corespondența

între variabila x și variabila

fdx concret avem 1 și următoare

și un număr corespunzător lui 1

este minus unu următoarea pereche

avem trei și F de 3 Adică 1 următoarea

pereche avem șase și sd6 adică

patru e bine mulțimea formată din

aceste elemente reprezintă de fapt

graficul funcției f Deci graficul

funcției este de fapt o mulțime

acum elementele acestei mulțimi

ce formă au precum am găsit noi

elementele Iată avem aici x a fost

1 iar minus unu e de fapt fd1 Deci

avem perechea 1 și F de 1 următoarea

pereche este 3 și 1 care este f

de 3 Deci avem 3 și e f de 3 iar

Aici avem de fapt 6 și F de 6 graficul

unei funcții este o mulțime formată

din elemente de această formă x

și f de x avem asemenea perechi

cu proprietatea că x parcurge domeniul

de definiție al funcției adică

aparține Domeniului de definiție

și chiar o să trec aici că această

mulțime o Vom nota cu D de la domeniul

de definiție graficul unei funcții

este prin urmare o mulțime de această

formă e puțin derutantă denumirea

pentru că te aștepta ca de fapt

graficul unei funcții să fie o

reprezentare pentru un desen însă

noi știm că aceste perechi se pot

reprezenta geometric de aceea ca

să nu Ne încurcăm foarte mult în

denumiri prin graficul unei funcții

vom înțelege o mulțime adică mulțimea

de această formă dar în același

timp vom înțelege și reprezentarea

geometrică a acestei înmulțiri

Păi Haideți să Reprezentăm cele

trei puncte între un sistem de

coordonate și trasă în două axe

perpendiculare avem aici axa orizontală

o axă pe verticală Deci cele două

axe sunt perpendiculare avem aici

axa o x axa absciselor axa o y

axa ordonatelor o este originea

sistemului de axe ne alegem și

o unitate de măsură Să considerăm

că acest că lungimea acestui segment

este unitatea de măsură și trecem

punctele avem aici punctul de coordonate

1 și minus unu unu se află pe axa

absciselor deci pe o x trecem aici

1 iar minus unu se află pe axa

o y Adică cum treci aici sub zero

la o unitate distanță față de originea

sistemului de axe de ce avem aici

minus 1 și găsim acest punct avem

aici asa 3 ordonată 1 deci pe o

x găsim pe trei Avem doi trei aici

și pe o trecem pe 1 adică aici

găsim și acest punct Iată acesta

și mai avem abscisă 6 ordonată

4 de cel trecem pe 6 pe OLX avem

4 5 6 aici și pe oi cât trebuie

să trecem pe 4 2 3 4 și să găsim

și punctul bun Iată punctul este

acesta mult de fapt această linie

punctată trebuie să ajungă chiar

în dreptul lui 6 chiar o să desenăm

cu altă culoare acestei puncte

și prin trasarea acestor puncte

avem și reprezentarea geometrică

a graficului funcției f Haideți

să mai facem încă un exemplu și

avem funcția f definită pe mulțimea

formată din elementele minus 3

minus 2 0 1 cu valori în mulțimea

Q mulțimea numerelor sonare Haide

x egal cu E bine aici avem o funcție

cu două ramuri legea de corespondență

se schimbă în funcție de valorile

variabilei x și avem HD x este

x plus 1 dacă x este strict mai

mic decât 0 și HD x este x supra

2 dacă x este mai mare sau egal

cu 0 casă tras în graficul mai

întâi vom face tabelul de Valori

și pe prima linie vom trece valorile

lui x pe a doua valorile funcției

Hash avem aici x HD x dacă x este

minus 3 să vedem ce vom avea poate

x să fie minus 2 0 și 1 dacă x

este minus 3 avem de calculat HD

minus 3 apoi HD minus 2 HD 0 și

mai avem HD un cât este HD minus

3 pe aici x este minus 3 adică

este un număr strig mai mic ca

0 minus 3 strig mai mic ca 0 Deci

HD minus 3 Cu cât va fi egal o

citim pe această ramură adică minus

3 plus 1 minus 3 a adunat cu unu

ne dă minus doi venim și trecem

aici minus 2 și chiar o să șterg

ca să nu avem să nu ne deruteze

calculul nostru dacă x este minus

2 HD minus 2 din o citim pe aceeași

ramură pentru că avem tot o valoare

negativă a lui x Deci o mai avea

minus 2 plus 1 adică minus 1 minus

1 avem acum x egal cu 0 hd0 Păi

unde citim vom avea a doua dacă

x este mai mare sau egal cu 0 aici

chiar este 0 Deci hd0 va fi acum

0 supra 2 0 supra 2 ne dă 0 venit

și trecem aici 0 și în final ultima

valoare avem de calculat hd1 în

voi scrie aici avem aceeași ramură

Adică 1 supra 2 și trecem 1 pe

2 dacă vrem să scriem graficul

funcției Haș atunci avem nevoie

de toate perechile de această formă

xhd x cu proprietatea că x aparține

Domeniului de definiție al funcției

și chiar putem să notăm aici că

această mulțime este de Marea notată

cu de mare graficul funcției h

este mulțimea formată din CP pe

aici Trebuie să parcurgă domeniul

de definiție Adică trebuie să luăm

aceste valori dacă x este minus

3 vom avea minus trei și minus

2 apoi avem perechea minus doi

minus unu apoi perechea formată

din numerele 0 și 0 și în final

avem 1 și 1 pe 2 și iată că am

notat și graficul funcției Hai

acum să facem și reprezentarea

geometrică a acestor puncte de

ce avem nevoie de un sistem de

coordonate trasăm aici două axe

perpendiculare avem axa absciselor

axa o x axa ordonatelor o y un

itatea de măsură notăm aici unitate

de măsură și să trecem punctele

minus 3 minus 2 avem minus trei

deci venim aici avem minus 1 minus

2 minus 3 și minus 2 pe axa o y

a d minus 1 minus 2 folosim acestei

linii punctate și găsim punctul

apoi minus 2 minus 1 deci pe axa

o x l alegem pe minus doi care

e aici pe axa o y minus unu trecem

pe minus 1 și găsim punctul care

e aici zero și zero adică avem

originea sistemului de axe chiar

o să trecem sau culoare se vadă

mai bine Bun avem aceste puncte

până acum mai avem nevoie de un

punct și anume avem abscisă 1 ordonată

1 supra 2 dacă aici este 1 atunci

1 pe 2 este aici avem unul pe doi

și iată că punctul pe care îl căutăm

este acesta să știți că putem să

și notăm punctele astfel acest

punct îl putem muta de exemplu

cu A mare El este un punct care

are abscisa minus 3 ordonata minus

doi Deci avem punctul A mare de

coordonate minus 3 minus 2 punctul

b mare are coordonatele minus 2

minus 1 este de fapt al doilea

punct care apare aici al treilea

punct este originea sistemului

de axe a avem coordonatele 0 și

0 Ilie notat deja cu o mare și

pe al patrulea să îl notăm cu ce

avem aici coordonatele 1 și ordonata

este 1 supra 2