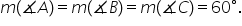Triunghiul echilateral

proprietățile triunghiului echilateral

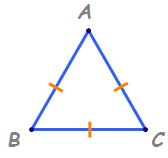
un triunghi care are toate laturile

congruente se numește triunghi

echilateral avem următoarea teoremă

nunți un triunghi echilateral toate

unghiurile sunt congruente având

măsura egală cu 60 de grade vom

face demonstrația acestei teoreme

Se știe că triunghiul abc este

echilateral Deci laturile sale

sunt congruente a b este congruentă

cu ac și congruentă cu bc și trebuie

să demonstrăm că unghiurile sunt

congruente unghiul a congruent

cu unghiul b congruent cu unghiul

c demonstrație având în vedere

că triunghiul echilateral are cel

puțin două laturi congruente înseamnă

că el poate fi privit ca pe un

triunghi isoscel dacă luăm în considerare

congruența segmentelor a b și a

c putem spune că triunghiul ABC

este un triunghi isoscel având

baza BC știind că triunghiul isoscel

are unghiurile de la bază congruente

Deci va rezulta că unghiul b este

congruent cu unghiul c notăm această

relație cu unu dacă ac este congruentă

cu bc Deci AC și BC atunci triunghiul

poate fi privit ca pe un triunghi

isoscel având baza ab Deci unghiurile

de la bază vor fi congruente Unghiul

ABC congruent cu unghiul b notăm

această relație cu doi putem observa

că dacă unghiul b este congruent

cu unghiul c și unghiul A este

congruent cu unghiul b A rezultat

din aceste două relații că unghiul

A este congruent cu unghiul și

congruente cu unghiul c Deci toate

cele trei unghiuri vor fi congruente

din relația 1 și 2 rezultă că unghiul

A este congruent cu unghiul b și

congruent cu unghiul c demonstrați

că triunghiul echilateral are toate

unghiurile congruente să vedem

cum putem arăta că ele au măsurile

egale cu 60 de grade din această

relație de congruență rezolv Dacă

măsura unghiului a este egală cu

măsura unghiului b și egal mai

departe cu măsura unghiului c dar

știm că în orice triunghi suma

măsurilor unghiurilor este egală

cu 180 de grade Așadar voi scrie

că măsura unghiului A plus măsura

unghiului b plus măsura unghiului

c egal cu 180 de grade din aceste

două relații mai rezulta următoarea

relație măsura unghiului a plus

lung de măsura unghiului b și măsura

unghiului c Putem să scriem măsura

unghiului A pentru ca aceste măsuri

sunt egale eu și măsura unghiului

a egal cu 180 de grade 3 ori măsura

unghiului a egal cu 180 de grade

împărțim această egalitate la 3:00

în ambii membri și rezultă că măsura

unghiului a va fi egală cu 180

de grade împărțit la 3 egal cu

60 de grade așadar am arătat că

cele trei unghiuri sunt congruente

și au măsurile de 60 de grade scrie

că măsura unghiului a este egală

cu măsura unghiului b egal cu măsura

unghiului C egal cu 60 de grade

următoarea teoremă Dacă un triunghi

are toate unghiurile congruente

atunci triunghiul este echilateral

aceasta este teorema reciprocă

a teoremei anterioare pentru a

demonstra de exemplu ca un triunghi

este echilateral putem să aplicăm

această teoremă și Să arătăm că

el are toate unghiurile congruente

o consecință a acestor teoremei

este următoarea proprietate un

triunghi isoscel care are un unghi

cu măsura de 60 de grade este triunghi

echilateral este valabilă și următoarea

teoremă întru un triunghi echilateral

toate liniile importante ce pornesc

din același vârf coincid cele trei

bisectoare sunt și mediane înălțimi

și mediatoare orice triunghi echilateral

poate fi considerat un triunghi

isoscel Așadar toate proprietățile

triunghiului isoscel se aplică

și în cazul triunghiului echilateral

și mai mult proprietățile referitoare

la liniile importante în triunghi

sunt valabile pentru fiecare latură

a acestui triunghi dacă a m este

bisectoare ia va fi și mediana

înălțime și mediatoare la fel si

pe va fi bisectoare mediană înălțime

și mediatoare respectiv bn va fi

și ia bisectoare mediană înălțime

și mediatoare Așadar cele trei

linii importante ce pornesc din

același vârf coincid observăm că

și punctul de intersecție al acestora

este în același timp ortocentru

centru de greutate centrul cercului

înscris în triunghi și centrul

cercului circumscris triunghiului

cele trei segmente a m b n și c

p vor fi și axe de simetrie triunghiul

echilateral este triunghiul cu

cele mai multe axe de simetrie

acest triunghi are trei axe de

simetrie în continuare o să facem

două probleme prima problemă triunghiul

abc este echilateral si ad perpendiculară

pe bc d aparține segmentului BC

dacă BC este 3 cm Calculați perimetrul

triunghiului ABC Bă scrie ipoteza

se dă un triunghi abc echilateral

asta înseamnă că AB este congruent

cu ac și congruentă cu bc Se știe

că AD este perpendiculară pe BC

Așadar ad este înălțime se știe

că DC este 3 cm mai scrie și pe

figura d c 3 cm trebuie să calculăm

perimetrul triunghiului ABC demonstrație

având în vedere că ad este înălțime

și triunghiul ABC este echilateral

rezultă că AD este și mediană și

atunci punctul D este mijlocul

segmentului BC Dacă d este la mijloc

înseamnă că b d este congruent

cu d c b d va avea aceeași lungime

cu dc și numele 3 cm ma rezultat

că latura bc va avea 6 cm iar triunghiul

fiind echilateral toate cele trei

laturi vor avea aceeași lungime

de 6 centimetri Moon calcula perimetrul

acestui triunghi însumând cele

trei laturi Adi fiind perpendiculară

pe b c și triunghiul a b c fiind

un triunghi echilateral va rezulta

că AD este și mediană rezultă că

BD va fi egal cu DC și egal cu

3 cm Lungimea segmentului BC se

calculează însumând cele două segmente

bd și DC egal cu 3 cm plus 3 cm

egal 6 cm ma rezultat că și AB

respectiv AC vor avea aceeași lungime

de 6 cm și acum calculăm perimetrul

acestui triunghi însumând cele

trei laturi perimetrul triunghiului

ABC mafin egal cu ab plus AC plus

BC egal mai departe cu 6 plus 6

plus 6 cm egal cu 18 cm și următoarea

problemă În triunghiul dreptunghic

ABC cu măsura unghiului BAC egală

cu 90 de grade prelungim Ba cu

AD congruent cu AB Dacă măsura

unghiului ACB este egală cu 30

de grade Arătați că triunghiul

b d c este echilateral prelungim

segmentul Ba cu un alt segment

congruent cu acesta a d Se știe

că măsura unghiului b c a este

de 30 de grade și trebuie să arătăm

că triunghiul bcd este echilateral

o modalitate de a arăta că triunghiul

b d c este echilateral este Să

arătăm că acesta este un triunghi

isoscel care are un unghi cu măsura

de 60 de grade pentru a arăta că

triunghiul bcd este isoscel vom

arăta că acesta are două laturi

congruente mai exact demonstrăm

că bc va fi congruentă cu cd la

trebui să încadrăm aceste două

segmente în două triunghiuri vom

demonstra că triunghiul b a c este

congruent cu triunghiul d a Ce

observăm că acestea sunt triunghiuri

dreptunghice măsura unghiului BAC

fiind de 90 de grade va rezultată

și măsura unghiului dac este tot

de 90 de grade pentru că acestea

sunt unghiuri suplementare Așadar

vom compara Două triunghiuri dreptunghice

știm din ipoteză că AD este congruent

cu AB a d și a b sunt catete în

cele două triunghiuri acestea mai

au o latură comună aceasta este

cateta AC AC este congruent cu

ac endo latură comună din cele

două relații rezultă conform cazului

de congruență catetă catetă că

triunghiul de ac este congruent

cu triunghiul BAC iar din congruență

acestor două triunghiuri va rezulta

că de ce este congruent cu b c

am arătat că acest triunghi are

două laturi congruente înseamnă

că el va fi un triunghi isoscel

rezultă pe triunghiul cdb este

un triunghi isoscel acum mai trebuie

să arătăm că acesta are un unghi

cu măsura de 60 de grade din congruența

celor două triunghiuri va rezulta

și că unghiul de ce a este congruent

cu unghiul BCA înseamnă că și acest

unghi va avea măsura de 30 de grade

și atunci putem Observa cu ușurință

că măsura unghiului d c b este

de 60 de grade iar un triunghi

isoscel care are un unghi cu măsura

de 60 de grade este triunghi echilateral

din faptul că triunghiul d a c

este congruent cu triunghiul BAC

ma rezultă că unghiul de ce a este

congruent cu unghiul BCA rezultă

că măsura unghiului DCA este egală

cu măsura unghiului b c a și de

el mai departe cu 30 de grade putem

să aflăm acum măsura unghiului

dcb aceasta va fi egală cu 30 de

grade plus 30 de grade egal cu

60 de grade am arătat că triunghiul

este isoscel notăm această relație

cu unu și am arătat că acest triunghi

are un unghi cu măsura de 60 de

grade din relația 1 și 2 ma rezultat

că triunghiul cdb este echilateral

există și o altă modalitate de

a demonstra că acest triunghi este

isoscel fără să folosim metoda

triunghiurilor congruente dacă

ne uităm pe figura observăm că

c a este înălțime în triunghiul

cde b pentru că c a este perpendiculară

pe BD știm din ipoteza ca aceste

două segmente a b și a d sunt congruente

înseamnă că c a este și mediană

iar un triunghi în care o înălțime

coincide cu mediană este triunghi

isoscel dacă a este înălțimea și

mediană atunci ea este și bisectoare

de unde ar fi rezultat că unghiul

b c A este congruent cu unghiul

b c a d semne că acesta are măsura

de 30 de grade