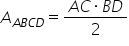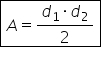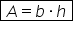Aria rombului

în lecția aceasta o să deducem

o formulă de calcul pentru aria

rombului rombul este prin definiție

un paralelogram cu două laturi

consecutive congruente la lecția

respectivă am de dus câteva proprietăți

ale rombului și anume laturile

rombului sunt congruente și diagonalele

acestuia sunt perpendiculare având

în vedere că rombul este un paralelogram

particular pentru calculul ariei

acestuia putem folosi în primul

rând formula de calcul de la aria

paralelogramului dacă ducem o înălțime

în acest romb Adică o perpendiculară

din vârf pe o latură opusă atunci

o formulă de calcul pentru aria

rombului ar putea fi baza ori înălțimea

bază este latura ABC iar înălțimea

în cazul acesta Este DM în continuare

ne propunem să deducem și o altă

formulă de calcul pentru aria rombului

atunci când se cunosc diagonalele

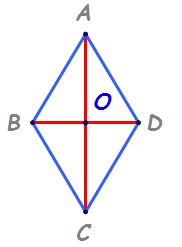
acestuia să construim diagonalele

acestui romb AC și BD observăm

că se au format două triunghiuri

Triunghiul ABD și triunghiul bcd

și atunci aria rombului se poate

scrie ca suma celor două arii scrie

că aria rombului a b c d este formată

din a aria triunghiului ABD plus

aria triunghiului bcd În triunghiul

ABD AO este înălțime pentru că

diagonalele rombului sunt perpendiculare

iar BD este baza triunghiului și

atunci Putem să scriem că aria

triunghiului ABD este semi produsul

dintre bază și înălțimea acestuia

adică BD ori a o supra 2 iar aria

triunghiului bcd va fi BD orice

o supra 2 Avem două fracții cu

același numitor la numărător om

scrie BD ori a o Plus BD orice

o totul supra doi egal în continuare

la numărător putem se dă factor

comun pe BD obținem BD pe lângă

ei o plus si o supra 2 Dar AO plus

c o formează segmentul AC egal

cu bd ori ace supra 2 bd și ac

sunt diagonale în acest romb și

atunci Putem să scriem că Aria

rombului este semi produsul diagonalelor

m scrie de 1 diagonala 1 ori diagonala

2 supra 2 așadar am obținut cu

a doua formulă de calcul pentru

aria unui romb atunci când se cunosc

diagonalele acestuia aria este

diagonala 1 ori diagonala 2 supra

2 această formulă se poate aplica

pentru orice patrulater convex

care are diagonalele perpendiculare

Și acum să facem o aplicație o

problemă Un romb are diagonalele

de 6 cm 8 cm și latura egală cu

5 cm Calculați la punctul a aria

rombului iar la punctul B înălțimea

rombului să construim și noi diagonalele

În rombul a b c d având în vedere

că se cunosc acestei diagonale

pentru calculul ariei rombului

va folosi a doua formulă pe care

am de dus o mai devreme aria lui

a b c d va fi sânii produsul diagonalelor

ace ori b d supra 2 egal cu 8 ori

6 supra 2 egal cu 48 supra 2 și

egal cu 24 cm pătrați iar la punctul

B trebuie să aflăm înălțimea rombului

să construim o înălțime ducem de

exemplu perpendicularei din d pe

ab trebuie să aflăm lungimea segmentului

de m pentru aceasta va folosi prima

formulă de calcul pentru aria rombului

rombul fiind un paralelogram rer

se se poate scrie ca fiind produsul

dintre o latură și înălțimea corespunzătoare

ei Deci aria rombului a b c d este

baza ab ori bem dar nu Am calculat

deja aria anterior Deci această

relație a b ori dm se poate egala

mai departe cu 24 no să mai scriu

centimetri pătrați știind că latura

rombului este egală cu 5 cm Deci

AB este 5 din ipoteză și atunci

deducem următoarea relație 5 ori

dm va fi egal cu 24 de unde rezultă

că de m este egal cu 24 împărțit

la 5 după ce facem un simplu calcul

obținem rezultatul 4 cm Așadar înălțimea

rombului va fi egală cu 4 cm