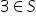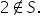Definiția mulțimilor. Proprietatea de apartenență a unui element la o mulțime
Tag-uri
Partajeaza in Google Classroom

Transcript
să vedem în continuare Ce este
aceea o mulțime și Ce înțelegem
prin apartenența unui element la
o mulțime o mulțime este o colecție
o grămadă de obiecte atenție distincte
Ce înseamnă distincte adică diferite
Păi avem aici obiecte diferite
sigur avem o minge de tenis una
de baschet una de ping pong și
una de volei asta înseamnă că ce
avem aici poate fi considerată
o mulțime bun Haideți să dăm un
alt exemplu să vedem acum dacă
ce avem aici este tot așa o mulțime
ce trebuie să vedem dacă obiectele
sunt distincte Păi pe lângă obiectele
enumerate înainte am adăugat un
fluturaș de badminton din Noua
avem obiecte distincte asta înseamnă
că și Aceasta este o mulțime dar
ce avem aici Păi pe lângă aceste
obiecte am adăugat un minge de
ping pong atenției identică cu
cea care era inițial Păi mai avem
aici o mulțime nu deci putem să
notăm că nu este mulțime de ce
Pentru că mulțimea presupune existența
unor obiecte distincte și cu noi
avem două mingi de ping pong identice
clar ce avem aici nu e un mulțime
Cum se notează acum mulțimile a
mulțimea este Notează cu litere
mari de tipar de exemplu această
mulțime o putem nota cu M mare
de la mulțime și pe aceasta obtinuta
cu altă literă exemplu amare acum
Toate aceste obiecte se numesc
ele mint A deci e element al mulțimii
m este și mingea de tenis și mingea
de volei și mingea de însă și cea
de ping pong la fel elementele
mulțimii A sunt pe lângă aceste
patru tipuri de mingi și fluturașul
de badminton acum cum Reprezentăm
mulțimile Păi o mulțime poate fi
reprezentată cu ajutorul unei diagrame
Ce este aceea o diagramă pe este
un desen asemănător cu acesta care
cu ajutorul căruia descrie mulțimea
respectivă Deci ca o prima modalitate
notăm reprezentarea cu ajutorul
diagramelor și Haideți să notăm
aici că vorbim de mulțimea pe care
a mutat o inițial de mare o altă
modalitate de reprezentare a unei
mulțimi de cea de a doua modalitate
este prin enumerarea elementelor
mulțimii a adică trecem elementele
din această mulțime iată le am
trecut aici Nu contează atenție
ordinea de scriere a elementelor
de să le trecem În ce ordine dori
atâta timp cât vom trece punct
și virgulă între elemente și toate
elementele le trecem între acolade
și spunem că mulțimea notată de
noi e mare este mulțimea formată
din elementele mingea de timp mingea
de baschet mingea de volei și mingea
de tenis O a treia modalitate de
descriere de reprezentare a unei
mulțimi este prin enunțarea unei
proprietăți caracteristice elementelor
mulțimii pare destul de complicate
exprimarea însă care ideea trebuie
să scriem mulțimea m trebuie să
vedem Care este acea proprietate
care descrie elementele acestei
mulțimi și acum pentru exemplul
nostru ar trebui să inventăm o
poveste să spunem că acestea sunt
toate mingile lui Tudor Deci așa
că mulțimea m este formată din
acele elemente notate să le notăm
Generic elementele cu X putem să
trecem orice literă mică dorim
Dar în general se folosește litera
x Deci mulțimea M formată din elementele
x cu proprietatea să citim această
bară cu proprietatea că x este
cum am spus minge a lui Tudor Deci
Considerăm că Tudor nu are alte
mingi decât acestea Deci x este
minge a lui Tudor și când spunem
acest lucru că x a mingea lui Tudor
știind că vorbim de aceste patru
tipuri de mingi să mai facem acum
un exemplu format dintr o mulțime
care are ca elemente doar numere
pentru că de fapt cu acestea volu
craci cel mai mult și haide să
Reprezentăm mai întâi mulțimea
A cu ajutorul unei diagrame Deci
mulțimea formată din elementele
1 3 5 7 și 9 acum dacă am mai trece
aici elementul 5 ar mai avea o
mulțime nu pentru că nu am avea
toate elementele distincte ia Tom
avea de două ori numărul 5 Deci
nu facem acest lucru și să notăm
mulțimea să spunem că am o notăm
cu litera s mare Deci am reprezentat
cu ajutorul diagramei adică prin
prima metodă ce urmează a doua
metodă trebuie să enumerăm acum
elementele mulțimii Deci mulțimea
s este formată din aceste elemente
deschidem acolada și scriem elementele
mulțimii atenție în ce ordine dorim
Deci unu nouă trei șapte și cinci
acestea sunt elementele mulțimii
este care le am enumerat a treia
variantă Trebuie să găsim acum
o proprietate caracteristică elementelor
acestei mulțimi deja acum nu mai
e nevoie să inventăm nici o poveste
doar trebuie să fim atenți la elementele
mulțimii s Deci mulțimea s poate
fi descrisă prin această proprietate
Deci avem numerele 1 3 5 7 și 9
ce Observă păi în primul rând toate
sunt numere impare bun însă aici
avem toate numerele impare nu avem
doar pe acelea care sunt strict
mai mici ca 10 de fapt Avem doar
cifre impare asta înseamnă că mulțimea
A este formată din elementele x
Haide să ne notăm tot x cu proprietatea
că x este cum am spus cifră impară
Păi atunci când spunem că x este
cifră impară spunem chiar acestei
numere 1 3 5 7 și 9 acum aceasta
nu e singura variantă de scriere
a mulțimii putem să ne gândim și
astfel Deci x cu proprietatea că
x este număr impar Deci este număr
impar și pe lângă aceasta nu avem
aici toate numerele impare Deci
mai trebuie să punem o condiție
Păi trebuie să arătăm că el este
cifră ori scriem că x este strict
mai mic ca 10 sau mai mic sau egal
cu 9 oricare variantă Este corectă
acum Haideți să discutăm și despre
o notație am spus că fiecare obiect
al unei mulțimi se numește un element
poate să aparțină sau să nu aparțină
unei mulțimi de exemplu numărul
2 face parte din mulțimea s p este
2 cifre impar nu este o cifră în
să pară asta înseamnă că 2 nu face
parte din mulțimea s și notăm acest
lucru astfel trecem 2 și apoi facem
un e mai turtit pe care îl tăiem
cu o linie asta înseamnă că 2 nu
aparține așa citim nu aparține
mulțimii S3 În schimb face parte
din mulțimea A este o cifră impară
Deci notăm că 3 aparține descriem
aici aparține mulțimii s tot așa
un alt Exemplu un numărul 10 face
parte din mulțimea spre 10 este
cifră nu Asta înseamnă că 10 nu
aparține mulțimi s însă 7 de exemplu
aparține întradevăr mulțimii a
scoate cuvinte Haide să reținem
că omul schimb este o grămadă o
colecție de obiecte atenție distincte
adică diferite fiecare obiect se
numește element acum există elemente
care aparțin unei mulțimi și există
și elemente care nu aparțin mulțimii
respectiv dacă un element aparține
mulțimii folosim acest semn Cum
a fost aici dacă el nu aparține
atunci același semn îl vom tăia
cu o linie