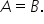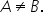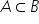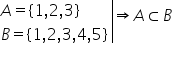Relații între mulțimi. Submulțimi

să vedem acum Ce relații se pot

stabili între mulțimi și ce este

aceea o submulțime Păi dacă avem

de exemplu aceste două mulțimi

mulțimea A E formată din elementele

avem o minge de ping pong fluturaș

de badminton o minge de baschet

și o minge de volei mulțimea B

observăm că de fapt are aceleași

elemente nu contează ordinea de

așezarea lor Păi când avem două

mulțimi care au aceleași elemente

spunem că cele două mulțimi sunt

egale deci putem să notăm că mulțimea

a este egală cu mulțimea b un alt

exemplu să luăm acum mulțimea a

c care este formată din elementele

2 9 5 și 4 și mulțimea de care

are ca elemente numerele 3 2 5

și 9 putem spune că cele două mulțimi

sunt egale Păi a lui Ali aceleași

elemente iată că de fapt aici avem

numărul 4 elementul reprezentat

de numărul 4 care nu se regăsește

în mulțimea de Sau invers aici

avem numărul 3 care nu face parte

din mulțimea C asta înseamnă că

cele două mulțimi c și d nu sunt

mulțimi egale și spunem că ele

sunt diferite Deci mulțimea ce

este diferită de mulțimea de acum

între două mulțimi în afară de

egal și diferit se mai pot stabili

și alte relații dacă avem mulțimile

m formată din elementele ce avem

aici unu doi cinci și mulțimea

să notăm cu p formată din elementele

cinci zero unu și doi Ce observăm

în legătură cu mulțimea m față

de mulțime Apelați puțin timp să

vă gândiți voi toate elementele

din mulțimea m se regăsesc în mulțimea

pe Iată primul element reprezentat

de numărul unu îl regăsim și aici

cinci îl regăsim și pe el în mulțimea

pe la fel se întâmplă și cu elementul

reprezentat de numărul 2 dacă vreți

putem să facem și o diagramă ca

să fie mai clar De exemplu avem

aici mulțimea m care conțin elementele

1 2 și 5 Deci aceasta e mulțimea

m și mulțimea pe care Pe lângă

aceste elemente 1 2 și 5 mai conține

și elementul 0 Deci aici avem mulțimea

pe Păi e clar că această mulțime

pe conține sau înghite să spunem

așa toată mulțimea m e bine când

se întâmplă acest lucru spunem

că mulțimea m Haideți să notăm

aici mulțimea m este inclusă în

mulțimea b și notăm cu acest si

turtit și citim inclusă în mulțimea

petreci mulțimea m inclusă în mulțimea

Putem să scriem și invers Deci

atenție când avem această notație

deschidere a semnului trebuie să

fie spre mulțimea care conține

mulțimea din stânga dacă vrem să

scriem Invers adică trece mai întâi

mulțimea pe și apoi mulțimea m

înseamnă că trebuie să scriem invers

și acest semn astfel încât deschide

să se păstreze tot către pe Deci

vom trece așa cum citim citind

că mulțimea B include mulțimea

m Deci aici avem inclusă și aici

avem include mulțimea m în aceste

situații Haideți să mutăm ce avem

aici în aceste situații când o

mulțime este inclusă întru altă

mulțime spunem că această mulțime

se numește submulțime a mulțimii

care o conține Aici nu am scris

submulțime Deci submulțime adică

mulțimea m este o submulțime a

mulțimii pe prin prescurtat așa

a lui pe un alt exemplu dacă avem

această x cu proprietatea că x

este pescăruș de pe Terra cu alte

cuvinte această mulțime descrie

reprezintă mulțimea tuturor pescărușilor

de pe planeta noastră Păi aceasta

ce aleg în Ce legătură este cu

această mulțime x cu proprietatea

că x este pasăre de pe Terra Păi

mulțimea pescărușilor de pe Terra

este inclusă în Deci hai desfacem

cu albi este inclusă în mulțimea

păsărilor de pe Terra Deci și aici

avem o submulțime acum Haideți

să mai facem uși încă să mai facem

încă un exemplu ca să lucrăm cu

aceste notații și avem mulțimea

A mare care este alcătuită din

elementele cinci nouă amic 11 și

o altă literă de exemplu ce Deci

avem o mulțime formată și din numere

și din litere mulțimea de mare

este formată din elementele 5 și

a mic și mulțimea ce mare este

formată din elementele a mic 9

și 5 altă literă b mic Ce relație

există între mulțimea A și mulțimea

b sau poate că e mai simplu să

scriem invers între mulțimea A

B și mulțimea A păi mulțimea B

conțin elementele 5 și a mic și

observăm că aceste două elementele

regăsim și în mulțimea A mare cu

orice element din mulțimea b se

regăsește în mulțimea A înseamnă

că mulțimea b este inclusă în mulțimea

A dacă am scris invers spunem că

a include mulțimea B acum Ce relații

există între mulțimea C și A să

notăm aici Deci întrece și A păi

Haideți să ștergem mai întâi ca

să nu Ne încurcăm munceam subliniat

și să vedem mulțimea ce are elementele

amic il gasim si aici și 9 este

și mulțimea A mare 5-ul regăsim

și pe el însă observăm că mai avem

aici elementul b mic care nu se

regăsește în mulțimea A ce înseamnă

asta mulțimea ce este inclusă în

mulțimea nu pentru că nu este conținută

în totalitate de mulțimea A atunci

spunem că ce nu este inclusă în

mulțimea A și acest semn îl tăiem

cu o linie recitim ce nu e inclusă

în mulțimea ta Haide să mutăm puțin

mai la stânga dacă vrem să scriem

Invers adică 1 mulțimea A și apoi

mulțimea a fi bun inverse acest

semn A nu include mulțimea C de

citim nu include mulțimea ce bun

Ce relații există acum între mulțimea

A B și C Deci b și c din nou vă

șterge aici Ce elemente sunt în

mulțimea B Păi avem cinci și a

pe care observăm că le regăsim

în mulțimea C de spunem că b este

inclusă în ce Sau invers mulțimea

ce include mulțimea b cu alte cuvinte

putem să notăm că mulțimea B aceasta

este o submulțime Deci b este o

submulțime a mulțimii C și tot

așa b este submulțime și a cărei

mulțimi A mulțimii A deci a lui

A iar dacă b este submulțime și

pentru ziua lui a și a lui Ce să

facem acum și două observații prima

observație Haideți să notăm aici

Observați Mulțimea vidă este inclusă

în orice mulțime de ce se inclusă

în mulțimea m oricare ar fi m mulțimea

deci putem să spunem că Mulțimea

vidă este submulțime a oricărei

mulțimi și atenție Deci mulțimea

vidă ce am notat aici deja este

o mulțime nu mai e nevoie să trecem

și acolade Deci nu folosim acest

semn în această situație mulțimea

vidă Deja e mulțime prin această

notație cea de a doua observație

se referă la o diferență de notație

și anume când vorbim de incluziune

folosim fie acest semn fie acesta

inclus și subiect mai avem o liniuță

aici poate să dăm un exemplu Când

folosim acest semn Păi mulțimea

1 2 este inclusă în mulțimea 1

2 7 Deci folosim acest semn atunci

când toate elementele acestei mulțimi

sunt conținute în această mulțime

și atenție cele două mulțimi nu

sunt egale Deci mulțimea formată

din elementele 1 2 este diferită

de mulțimea formată din elementele

1 i7 Clark la nu sunt egale aici

citim inclus sau egal Acest semnal

putem folosi și în această situație

deci putem să spunem că mulțimea

1 2 din formată din elementele

1 2 este inclusă sau egală cu mulțimea

formată din elementele 1 2 7 însă

dacă avem acest exemplu mulțimea

formată din elementele 1 2 este

inclusă sau egală cu mulțimea formată

din aceleași elemente 1 2 deci

în situația în care cele două mulțimi

sunt egale cu ma bem aici Deci

aceste două mulțimi sunt de fapt

egal atunci nu folosim acest semn

cellphone folosit pe acesta inclus

sau egal asta ne arată faptul că

mulțimea formată din elementele

1 2 poate fi privită ca o submulțime

a aceleiași mulțimi formată din

aceleași elemente Deci folosim

acest semne putem folosi întotdeauna

și în această situație și în aceasta

când avem mulțimea egal însă pe

acesta în nu îl folosim deci nu

îl folosim în situația în care

mulțimile sunt egale Haideți să

facem acum o recapitulare ca să

nu Ne încurcăm în notații deci

între un element și o mulțime Avem

doar relație de apartenență Deci

un element poate să aparțină unei

mulțimi sau poate să nu aparțină

unei mulțimi între două mulțimi

însă nu mai avem relație de apartenență

că aici ce avem relație de incluziune

Deci o mulțime este inclus întru

altă mulțime sau poate să nu fie

inclusă sau avem și varianta include

pe sau nu include pe el putem să

avem mulțimi egale sau mulțimi

diferite deci între două nu scriem

relație de apartenență și de incluziune

sau una din aceste variante ce

idee să dăm un exemplu elementul

3 aparține Oare aceste mulțimi

formată din elementele 3 6 și 8

sigur Deci avem 3 aparține acestei

mulțimi dar elementul 7 aparține

al aceleiași mulțimi formată din

aceste elemente pe șapte nu aparține

acestei mulțimi dacă avem însă

această scriere ce am notat aici

pe avem mulțimea formată din elementul

3 și aici avem aceeași mulțime

ca mai sus si notăm notăm faptul

că această mulțime aparține acesteia

nu această mulțime este inclusă

în aceasta pentru că elementul

3 se regăsește printre ele muntele

acestei mulțimi mulțimea formată

din elementul 7 acum este oare

inclusă în această mulțime i7 nu

se regăsește printre aceste elemente

Deci această mulțime nu este inclusă

în aceasta Deci ai de să ne fie

foarte clar că atunci când vorbim

de relații între un element și

o mulțime Avem doar aparține sau

nu aparține între două mulțimi

însă putem să avem una din aceste

variante și acum Haideți să facem

un ultim exercițiu în care să folosim

Toate aceste notații am scris notațiile

nu le vom folosi chiar pe toate

Haide să vedem Să completăm pentru

primul exercițiu patru puncte puncte

și niște de aici mulțimea formată

din elementele 5 4 0 avem aici

Păi avem un element și aici o mulțime

deci putem să alegem între aparține

sau nu aparține Cum elementul 4

se regăsește în mulțime înseamnă

că 4 aparține acestei mulțimi alt

exemplu ce am notat aici avem mulțimea

formată din elementul patru și

aici avem o altă mulțime aceeași

ca mai sus Păi avem acum două mulțimi

cum acest aliment se regăsește

în această mulțime înseamnă că

vom spune că prima mulțime este

inclusă Dar deci vorbim de relații

între două mulțimi este inclusă

în cea de a doua altă situație

5 și să luăm aici mulțimea A formată

din elementele 2 1 și 3 Păi avem

un element și o mulțime de ce alegem

dintre aceste Două semne cinci

se regăsește printre elementele

acestei mulțimi Deci cinci nu aparține

acestei mulțimi alt exemplu avem

aici mulțimea formată din elementul

0 și aici mulțimea dată inițial

cinci patru armată din elementele

cinci patru și zero Păi din nu

avem o relație între două mulțimi

0 se regăsește și aici Deci avem

relație de incluziune mulțimea

formată din elementele 2 1 3 și

aici avem mulțimea formată din

elementele 1 și 2 Păi această mulțime

conține elementele acestei mulțimi

cum notăm înseamnă că această mulțime

include mulțimea formată din elementele

1 copii doi Deci deschiderea semnului

este către mulțimea care este care

conține mulțimea în trecut aici

în dreapta încă un exemplu mulțimea

vidă și avem aici mulțimea formată

din elementul 0 si Cum trece între

cele două mulțimi pe putem noi

oare să trecem egalitate pe mulțimea

vinde este mulțimea care nu are

niciun element însă aici avem o

mulțime care are un element Nu

contează că el este 0 Deci aceste

două mulțimi nu pot fi egal ce

putem însă să spunem întotdeauna

despre mulțimea Vidra că ea este

inclusă în orice mulțime și să

mai luăm încă un exemplu mulțimea

formată din elementele 5 4 și 0

și mulțimea formată din elementele

45 mai avem aceleași elemente înseamnă

că vorbim de mulțimi egale cu acest

exercițiu am încheiat Sper că sa

înțeles modul de folosire al acestora

semne