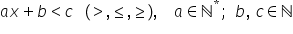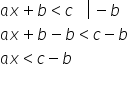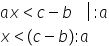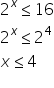Inecuații în mulțimea numerelor naturale

în continuare vom învăța să rezolvăm

inecuații Ce este aceea o inecuatie

Păi dacă intru ecuație în loc de

semnul egal trecem unul din aceste

semn strig mai mic sau strig mai

mare mai mic sau egal sau mai mare

sau egal atunci ce vom obține va

fi o inecuatie de exemplu în loc

de x plus 2 egal cu 5 putem să

notăm x plus 2 strict mai mic decât

5 ce am obținut Aici este o inecuația

Cum rezolvam acum o inecuatie Păi

fie putem să rezolvăm prin încercări

însă cred că știți deja că această

rețetă nu e prea eficientă când

avem numere mai mari nu așa de

mici ca aici fi procedam întocmai

ca la ecuații însă în loc de semnul

egal vom respecta semnul inegalității

Păi Haideți să rezolvăm cum făceam

la ecuații noi vrem să determinăm

pe x având aici x plus 2 trebuie

practic să scădem scădem 2 din

această relație Deci trecem bara

verticală și scrie minus doi ce

vom avea avem aici x plus 2 minus

acest 2 este strict mai mic decât

5 din care îl scădem pe 250 ne

Haideți să mute aici ca să avem

semnele acest semn să fie unul

sub celălalt ce vom avea avem x

plus 2 minus 2 aici obținem 0 Deci

vom obține x plus zero adică x

strig mai mic decât 5 minus 2 3

bun care sunt acum numerele prime

mai mici decât 3 răspunsul este

depinde depinde de mulțimea în

care x ia valori astfel Haideți

să scriem aici dacă x este Deci

Prima variantă dacă x este număr

natural atunci Care sunt numerele

naturale strict mai mici ca 3 din

foarte ușor rezultă că x poate

fi și avem zero unu sau doi nu

putem să luăm și valoarea 3 pentru

că avem Strike mai mic decât 3

Dacă însă x este număr natural

x este un număr natural nenul atunci

x ce valori va lua el poate să

fie doar unul și doi pentru că

nu poate să ia valoarea 0 sau dacă

x este număr real despre acest

lucru O să învățăm mai târziu atunci

o să avem ceva de genul x aparține

intervalului deschis minus infinit

3 evident că despre acest lucru

Am discutat mai târziu să știi

că sunt și alte mulțimi Deci avem

și alte variante însă pentru început

noi vom lucra cu aceste două situații

în care x este fie număr natural

fie număr natural nenul pentru

exemplul nostru Haideți Să considerăm

prima în far yunta Deci x este

număr natural asta înseamnă că

el Ia valorile 0 1 sau 2 ce am

obținut aici aceste valori poartă

numele de soluție a inecuației

așa se întâmplă și la ecuații când

obținea am în această situație

concretă că x egal cu 3-a numărul

3 se numește soluția ecuației iar

Aici avem soluția inecuației bun

de ce aceste numere reprezintă

soluția inecuației pentru că dacă

îl Înlocuim pe x cu fiecare din

aceste valori comune propoziții

adevărate pe Haideți să facem verificarea

ca să ne obișnuim și cu inecuațiile

dacă x este 0 avem 0 plus 2 stick

mai mic decât 5 adică 2 este strict

mai mic A5 avem o relație adevărată

sigur dacă x este acum 1 avem 1

plus 2 strict mai mic ca 5 1 plus

2 înseamnă 3 este strict mai mic

decât 5 este dacă x este 2 vom

avea doi adunat cu doi strig mai

mic decât 5 adică patru este strig

mai mic decât 5 este și el din

nouă relație adevărată dacă x ar

fi 3 ce am obține Păi avem aici

3 plus 2 strict mai mic decât 5

adică 5 este strict mai mic decât

5 nu avem aici o relație falsă

Deci nu am oprit în acest moment

înseamnă că x poate să fie doar

zero unu sau doi Deci ce am notat

aici vom șterge Haideți acum să

rezolvăm și alte inecuații și avem

13 adunat cu x mai mare sau egal

cu 20 unde Considerăm că x este

număr natural Deci căutăm toate

numerele naturale care verifică

această relație cum a spus la început

putem să căutăm soluția prin încercări

adică vedem dacă x egal cu 0 verifică

cu alte cuvinte 13 plus 0 este

mai mare sau egal cu 20 nu e o

relație farsă merge mai departe

13 plus unu luăm pe x egal cu unu

e mai mare sau egal cu 20 mici

acum naiba relația adevărată și

așa mai departe până când începem

să găsim soluția însă e clar că

această variantă de rezolvare nu

este una eficientă și pierdem foarte

mult timp de aceea vom rezolva

inecuațiile așa cum am învățat

la ecuații având aici 13 plus x

și vrem să ne rămână doar x înseamnă

că ce avem de făcut Trebuie să

scădem din această sumă pe 13 Deci

Scrie boala verticală notăm minus

13 asta înseamnă că vom scădea

și din 20 pe 13 și vom obține 13

plus x minus 13 este mai mare sau

egal cu 20 din care scădem pe 13

un ce avem aici pe 13 plus x știind

că adunare comutativă a avea de

fapt x plus 13 minus 13 aici ne

dă 0 d x plus 0 cu alte cuvinte

vom obține x este mai mare sau

egal cu 20 minus 13 adică 7 cu

alte cuvinte si vom obține numerele

naturale mai mari sau egale cu

7 sunt Deci x poate fii luăm pe

7 mai întâi 8 9 10 și așa mai departe

2015 citrat de fapt avem o infinitate

de Valori pentru x atenție doar

acestea sunt numerele naturale

care verifică această inecuația

acestea sunt singurele numere naturale

care verifică relația dată și vorbim

de o infinitate de numere o altă

inecuației x minus nouă notăm aici

stick mai mic decât 8 cum determinăm

pe x o y dacă avem aici x minus

nouă ca să ne rămână în această

parte inegalității doar x înseamnă

că trebuie să îl adunăm pe 9 Deci

notăm bara verticală și scrie în

plus 9 și vom avea x minus 9 plus

9 acesta este strict mai mic decât

8 la care îl adunăm pe 9 și vom

obține aici dacă din x scădem noua

apoi adunăm tot 9 vom obține îl

vom obține pe x mai mic strict

decât 17 Cât este atunci x Considerăm

la fel x număr natural Deci x poate

fi avem cel mult de fapt cel mult

16 pentru că nu putem să mergem

până la 17:00 chestii strig mai

mic de cinci pandy 0 1 2 și așa

mai departe Neo prim la 16 acestea

sunt singurele numere naturale

care verifică această inecuația

mate exemplu 4 x cu alte cuvinte

4 înmulțit cu x strict mai mare

decât 60 dacă aveam aici o ecuație

cum procedam am fi avut patru ori

x egal cu 60 atunci spuneam că

x este egal cu 60 împărțit la 4

la fel se întâmplă și la inecuații

doar că notăm x este acum strig

mai mare Deci nu egal cu 60 împărțit

la 4 practic am împărțit această

inegalitate la 4:00 ne neapărat

nevoie să scriem și sub această

formă putem să notăm direct și

obținem că x este strict mai mare

decât 60 împărțit la 4 înseamnă

15 Care sunt valorile lui x Haide

să trecem aici x este număr natural

x poate fi Cu ce valoare începem

cu 15 nu pentru că x este strict

mai mare decât 15 Deci pornind

de la 16 și avem 16 17 18 19 20

și așa mai departe Din nou avem

o infinitate de valori de numere

naturale care verifică această

relație Deci toate numerele de

la 600 numerele naturale de la

16:00 încolo verifică această inegalitate

această inecuației un alt exemplu

avem acum x înmulțit cu 21 mai

mic sau egal cu 105 îi putem să

notăm direct sau dacă vreți E clar

că trebuie să împărțim această

relație la 21 și vom avea x ori

21 împărțit la 21 ne va da de x

mai mic sau egal cu 105 împărțit

la 21 Deci x este mai mic sau egal

facem împărțirea și obținem 5 din

nou Considerăm că x este număr

natural cu alte cuvinte x poate

fi ce valori naturale sunt mai

mici sau egale cu cinci pornind

de la 0 1 2 3 4 5 și neam oprit

acestea sunt singurele numere naturale

care verifică relația dată încă

un exemplu și Ade să luăm acum

x împărțit la un număr să fie el

7 strict mai mare decât 6 dacă

aveam o ecuație Adică o egalitate

aici cum rezolvam spuneam că x

este egal cu 6 ori 7 la fel se

întâmplă și aici avem x este acum

strig mai mare decât 6 înmulțit

cu 7 de fapt această relație un

mulțimi cu 7 având x împărțit la

7 ori 7 vom obține x strig mai

mare decât șase ori șapte ce avem

aici și să notăm obținem că x este

strict mai mare decât 42 Cât poate

să fie x atunci x poate fi din

nou avem o infinitate de Valori

începem de la cât de la 43 și avem

43 44 45 și așa mai departe fiecare

număr dintre acestea deci de la

43 încolo împărțit la 7:00 o să

ne dea un număr natural sau nu

strig mai mare decât șase Haideți

să complicăm acum puțin lucrurile

și avem ecuația 3x cu alte cuvinte

3 înmulțit cu x minus 11 mai mic

sau egal cu 25 Cum procedam la

ecuații Păi nu putem să separăm

de la început pe 3D x pentru că

între ele avem operația de înmulțire

Deci mai întâi vom obține o relație

legată de trei ori x asta înseamnă

că pentru a obține pe 3 ori x Ce

trebuie să facem având aici 3x

minus 11 înseamnă că trebuie să

adunăm 11 în această relație și

vom obține 3 x adică trei ori x

minus 11 adunat cu 11 este mai

mic sau egal decât 25 plus 11 și

facem calculul aici ajungem la

3 ori x Deci notăm direct mai mic

sau egal cu obținem aici 36 Păi

cum avem aici înmulțire înseamnă

că trebuie să împărțim această

relație Acum la 3:00 ca să îl obținem

pe x și vom avea că x este mai

mic sau egal cu 36 împărțit la

trei de x este mai mic sau egal

cu 12 Care sunt valorile deci putem

să notăm și x ia valorile Haideți

acum Să considerăm că x este număr

natural dar să spunem că el este

nenul Până acum am lucrat cu x

număr natural acum Considerăm și

că el este nenul deci el nu poate

să ia valoarea 0 începem prin urmare

de la cât de la 1 ce avem 1 2 3

căutăm numerele naturale mai mici

sau egale cu 12 Deci 11 12 și în

acest moment în neam oprit acestea

sunt singurele numere naturale

care verifică relația dată să rezolvăm

acum o altă in ecuație și Considerăm

că x este un număr natural și vrem

să rezolvăm această inecuației

2 la x Deci necunoscută este acum

exponentul acestei puteri mai mic

sau egal cu 16 în general putem

să rezolvăm aceste tipuri de inecuații

prin încercări cu alte cuvinte

vedem dacă x egal cu 0 verificăm

această relație Deci Haideți Să

montăm 2 la 0 este mai mic sau

egal cu 16 Dar 2 la 0 este 1 este

mai mic sau egal cu 16 mai departe

dacă x este 1 2 la 1 Yannis semne

2 și este întradevăr mai mic sau

egal cu 16 Deci din nou relații

adevărată 2 la a doua este mai

mic sau egal cu 16 îi 2 la a doua

înseamnă 4 Care e mai mic decât

16 Deci din nou relație adevărată

2 la a treia este mai mic sau egal

cu 16 Dar pentru că 2 la a treia

este 8 Deci notăm din 9 aici relație

adevărată 2 la a patra îl luăm

acum pe x egal cu 4 este oare mai

mic sau egal cu 16 pe 2 la a patra

înseamnă 16 Care este mai mic sau

egal cu 16 iar își avem o relație

adevărată Haideți să ștergem 2

la a cincea Acum este mai mic sau

egal cu 16 pe 2 la a cincea înseamnă

32 care nu e mai mic sau egal cu

16 Deci această relație este una

falsă e bine de acum încolo pentru

valori ale lui x mai mari sau egale

cu 5 vom obține doar relații matematice

face asta înseamnă că XC valoria

Haide să notăm rezultă că x ia

valorile și avem așa 0 1 2 3 și

4 Deci notăm 0 1 2 3 4 și neam

oprit doar acestei valori însă

dacă avem numere mai mari cum rezolvăm

asemenea inecuații Păi rezolvarea

sintetică este următoarea Haide

să nu 2 la x mai mic sau egal cu

pe 16 îl putem scrie ca o putere

care are baza 2 sigur îl putem

nota 2 la a patra am văzut deja

acest lucru E bine în asemenea

situații în care bază este un număr

natural nenul diferit de 1 și atacă

în cazul nostru avem baza 2 2 este

un număr natural diferit de unu

de dacă se întâmplă acest lucru

și avem baze egale atunci inegalitatea

se trează și în cazul exponenților

deci practic avem această ecuație

deci de aici rezultă că x este

mai mic sau egal cu 4 cu acest

exponent și e clar că x fiind număr

natural rezultă sexy am obținut

aici valorile 0 1 2 3 sau 4 un

alt exemplu 7 la x plus 3 mai mare

sau egal cu 7 la 2015 Păi Haideți

să vedem baza este un număr natural

nenul diferit de 1 sigur 7 este

număr natural este diferit de 0

și diferit de unu este esențial

faptul că avem baze egal avem șapte

aici la fel și aici Bun cu alte

cuvinte este îndeplinită această

condiție Haideți să o denumim relația

a steluță am ieșit prea bine dar

înțelegeți punem între paranteze

atunci din rea ceastă relație din

relația steluță Ce rezultă că păstrăm

această acest semn și în cazul

exponenților Deci vom avea x plus

trei este mai mare sau egal decât

2015 și îl determină mă acum pe

x care este mai mare sau egal decât

2015 minus 3 Deci obține mai mare

sau egal cu 2012 cu alte cuvinte

x ia valorile numerele naturale

Considerăm tot așa că x a număr

natural mai mare sau egal cu 2012

Deci avem 2012 2013 2014 și așa

mai departe o infinitate de Valori

toate numerele naturale de la 2012

încolo verifică această relație