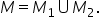Inecuații. Inecuații de gradul intai. Inecuații de gradul al doilea. Inecuații de gradul II cu modul
Tag-uri
Partajeaza in Google Classroom
Memorator: Inecuații. Inecuații de gradul intai. Inecuații de gradul al doilea. Inecuații de gradul II cu modul Descarcă PDF
Forma generală a inecuațiilor de gradul I cu o necunoscută este:
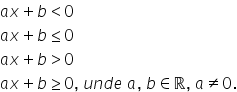
Valorile lui x pentru care se verifică inegalitatea se numesc soluții ale inecuației.
Pașii de rezolvare a inecuației de gradul I de forma ax + b < 0:
1. Scădem din ambii membri ai inecuației numărul b (sau îl trecem pe b în celălalt membru cu semn schimbat):
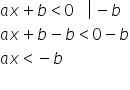
2. Împărțim ambii membri ai inecuației la a (a se mai numește coeficientul lui x):
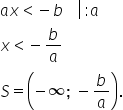
Atenție! Dacă înmulțim sau împărțim o inecuație cu un număr negativ, se schimbă semnul inegalității.
Soluția se va scrie sub formă de interval.
În mod analog se rezolvă și celelalte tipuri de inecuații.
Inecuații de gradul al doilea
Forma generală a inecuațiilor de gradul doi este:
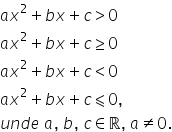
Rezolvarea inecuațiilor de gradul doi este o consecință imediată a semnului funcțiilor de gradul doi. Fie
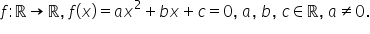
Semnul funcției de gradul doi se stabilește în funcție de semnul discriminantului și semnul lui a, astfel:
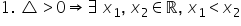
Funcția f are semnul lui a în afara rădăcinilor și semn contrar lui a între rădăcini. În consecință,
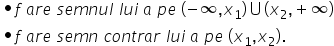
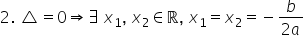
Funcția f are semnul lui a pe 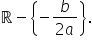
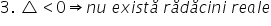
Funcția f are semnul lui a pe 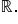
Pașii de rezolvare a unei inecuații de gradul doi:
- se rezolvă ecuația de gradul doi corespunzătoare inecuației date;
- se evidențiază semnul lui a;
- se stabilește în care dintre situațiile teoretice ne aflăm în raport cu delta;
- se stabilește mulțimea soluțiilor inecuației.
Inecuații de gradul al doilea cu modul
Explicitarea modulului unei inecuații de gradul doi se face astfel:
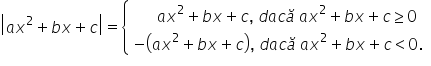
În continuare, pentru o mai bună explicitare a modulului, este necesar să rezolvăm inecuațiile ce se constituie drept condiții:
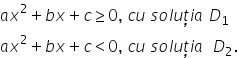
După determinarea domeniilor pentru fiecare din cele două situații, se trece la rezolvarea inecuației inițiale (vor fi două inecuații, câte una pentru fiecare situație). Soluțiile obținute pentru fiecare dintre cele două inecuații sunt intersectate cu domeniul de discuție al acestora. Astfel se obțin mulțimile de soluții ale inecuațiilor, notate cu
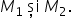
Soluția finala a inecuției cu modul se obține prin reuniunea celor două soluții: